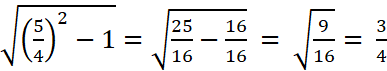Gleichungen

Gleichungen

Lineare Gleichungen

Lineare Gleichungen mit einer Variablen

Eine lineare Gleichung mit einer Variablen besteht aus zwei Termen mit einer Variablen, die durch ein Gleichheitszeichen miteinander verbunden sind.
Ergeben sich beim Einsetzen einer Zahl auf beiden Seiten der Gleichung die gleichen Termwerte, so nennt man die Zahl Lösung der Gleichung.

Beispiele:

(1) 4x + 3 = 15; Lösung x = 3, da 4٠3 + 3 = 15 (richtig, wahre Aussage)

(2) 6x – 14 = 2x + 10; Lösung x = 6, da 6٠6 – 14 = 22

Die Äquivalenzumformung ist die Umformung einer Gleichung, bei der sich die Lösung der Gleichung nicht ändert.
Dabei werden die Rechengesetze angewendet und es gilt:
Addition oder Subtraktion eines Terms oder einer Zahl auf beiden Seiten der Gleichung oder
Multiplikation mit einer Zahl ≠ 0 oder Division der Gleichung mit einer Zahl ≠ 0 ändert die Lösung nicht, sind also eine Äquivalenzumformung.

Schrittweise Lösung von Gleichung (2) durch Äquivalenzumformungen

6x – 14 = 2x + 10 | –2x

6x – 14 – 2x = 2x + 10 – 2x | + 14

4x – 14 + 14 = 10 + 14

4x = 24 | : 4

4x : 4 = 24 : 4

x = 6

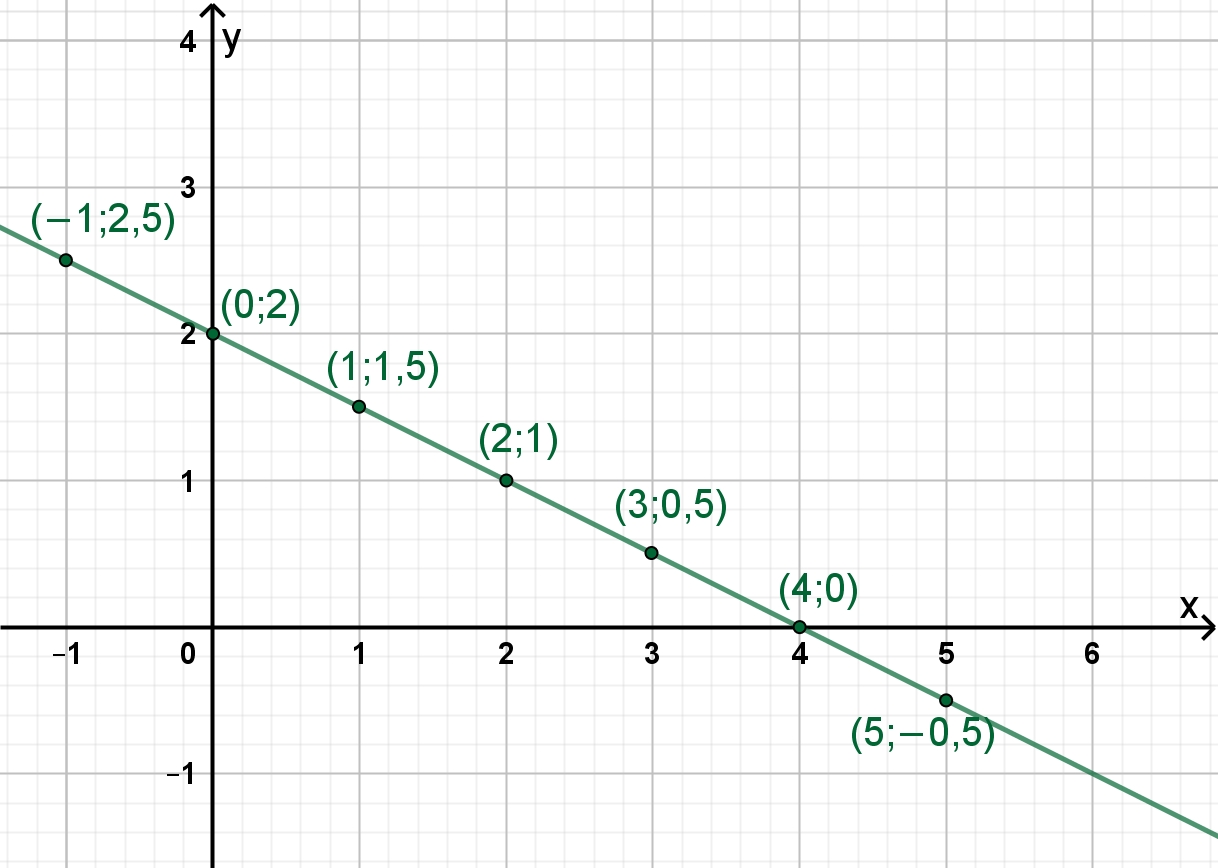
Lineare Gleichungen mit zwei Variablen

Beispiel:

x + 2y = 4

Es gibt unendlich viele Lösungen, die jeweils aus Zahlenpaaren (x;y) bestehen.

Beispiele: (1; 1,5) ist eine Lösung, da 1 + 2٠1,5 = 4 (richtig, wahre Aussage)
(3; 0,5) ist eine Lösung, da 3 + 2٠0,5 = 4 (richtig, wahre Aussage)

Die graphische Darstellung der Lösungsmenge ist eine Gerade.

Zwei lineare Gleichungen mit zwei Variablen

Beispiel 1:

I x + 2y = 4

II 3x – 4y = 2

Lösen mit dem Einsetzungsverfahren

I x + 2y = 4 | – 2y

I´ x = 4 – 2y

Einsetzen von I´ in II:

3 (4 – 2y) – 4y = 2

12 – 6y – 4y = 2 | – 12

–10y = –10 | : (–10)

y = 1

Einsetzen in I:

x + 2٠1 = 4 | – 2

x = 2

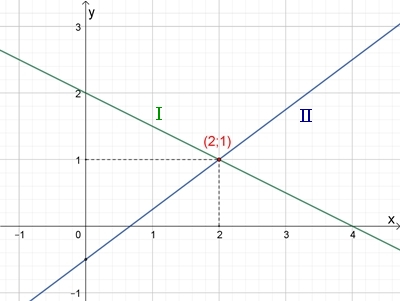
Lösung: (x, y) = (2; 1), Lösungsmenge L = {(2; 1)}

Graphische Darstellung der Geraden mit den Gleichungen I und II mit Lösung

Beispiel 2:

I 2x + 3y = 8,5

II 3x – 2y = 3

Lösen mit dem Additionsverfahren, Eliminieren von y

I 2x + 3y = 8,5 | ٠2

II 3x – 2y = 3 | ٠3

_________________

I´ 4x + 6y = 17

II´ 9x – 6y = 9

_________________

I´+II´ 4x + 9x + 6y – 6y = 17 + 9

13x = 26

x = 2

Einsetzen in I:

4 + 3y = 8,5 | – 4

3y = 4,5 | : 3

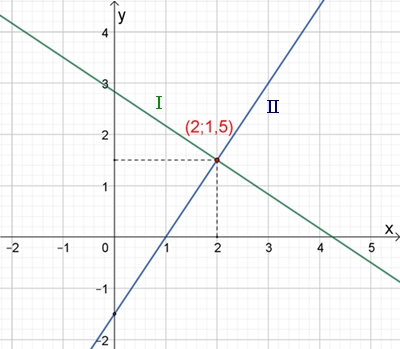
y = 1,5

Lösung: (x, y) = (2; 1,5), Lösungsmenge L = {(2; 1,5)}

Graphische Darstellung der Geraden mit den Gleichungen I und II mit Lösung

Beispiel 3:

I 2x + 3y = 5 | Gerade g1

II 4x + 6y = 8 | Gerade g2

_______________

2٠I – II 4x – 4x + 6y – 6y = 10 – 8

0 = 2 Widerspruch!

Daraus folgt: Es gibt keine Lösung, Lösungsmenge L = { }

Die zugehörigen Geraden g1 und g2 sind echt parallel

Beispiel 4:

I 2x + 3y = 5 | Gerade g1

II 4x + 6y = 10 | Gerade g2, II = 2٠I !

_______________

2٠I – II 4x – 4x + 6y – 6y = 10 – 10

0 = 0 wahre Aussage

Es gibt unendlich viele Lösungen, Lösungsmenge L = {(x, y) | 2x + 3y = 5}

(lies: „Menge aller Punkte x, y mit der Eigenschaft: 2 mal x plus 3 mal y ist gleich 5“)

Die zugehörigen Geraden g1 und g2 sind identisch.

Drei lineare Gleichungen mit drei Variablen (zur Vertiefung)

Beispiel 1: Gegeben sind die Gleichungen I, II und III

I 3x + 6y + 3z = 9,3

II 4x + 3y + 2z = 12

III 3x + 3y + 6z = 12

Lösen mit dem Additionsverfahren:

Eine Variable reduzieren, z.B. y :

2٠II – 1 = IV 8x – 3x + 6y – 6y + 4z – 3z = 24 – 9,3

II – III = V 4x – 3x + 3y – 3y + 2z – 6z = 12 – 12

__________________________________________

IV 5x + z = 14,7

V x – 4z = 0

_______________

Eine weitere Variable reduzieren, z.B. z:

4٠IV + V 20x + x + 4z – 4z = 58,8

21x = 58,8

x = 2,8

Einsetzen in V 2,8 – 4z = 0

z = 2,8 : 4 = 0,7

Einsetzen in II 4٠2,8 + 3y + 2٠0,7 = 12

3y = 12 – 11,2 – 1,4

3y = – 0,6

y = – 0,2

Lösung: (x, y, z) = (2,8; – 0,2; 0,7)

Veranschaulichung

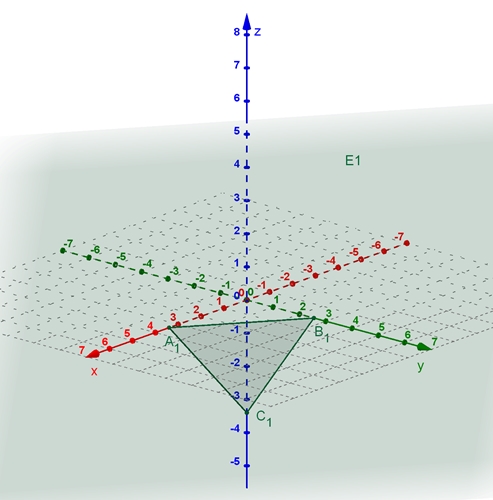
Jede der 3 Gleichungen I, II und III stellt im dreidimensionalen Raum jeweils eine Ebene E1, E2 und E3 dar:

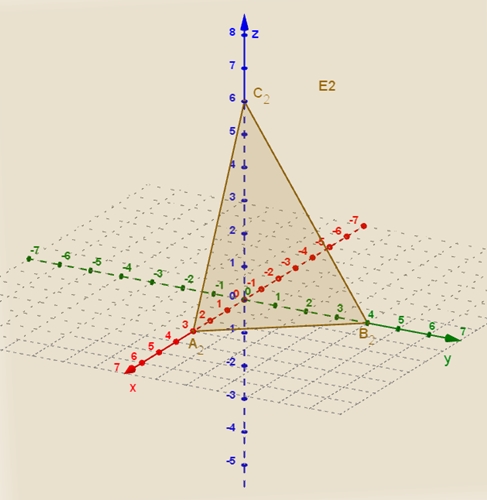
E1 : 3x + 6y + 3z = 9,3

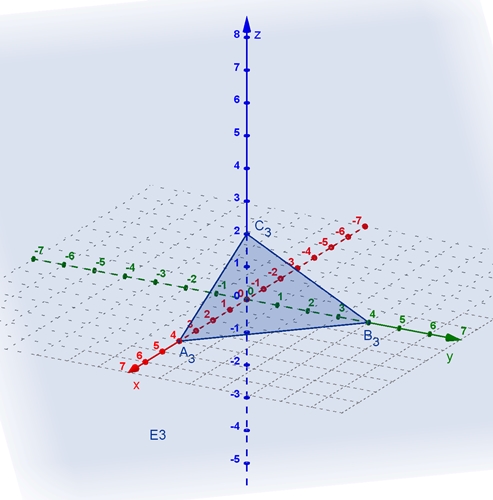
E2 : 4x + 3y + 2z = 12

E3 : 3x + 3y + 6z = 12

Die Lösung der 3 Gleichungen ist der Schnittpunkt der 3 Ebenen: S = (2,8; – 0,2; 0,7)

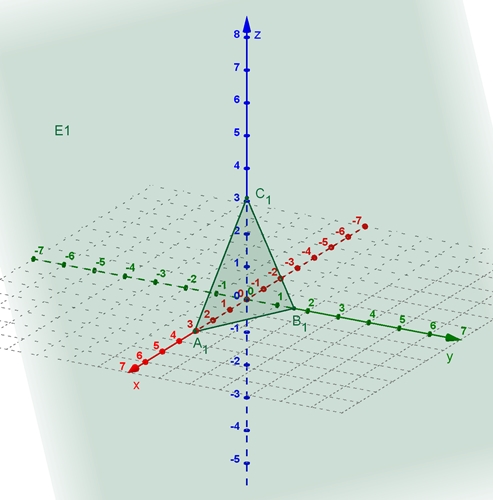
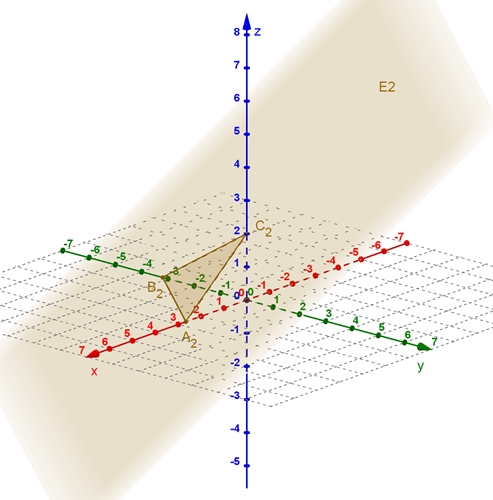
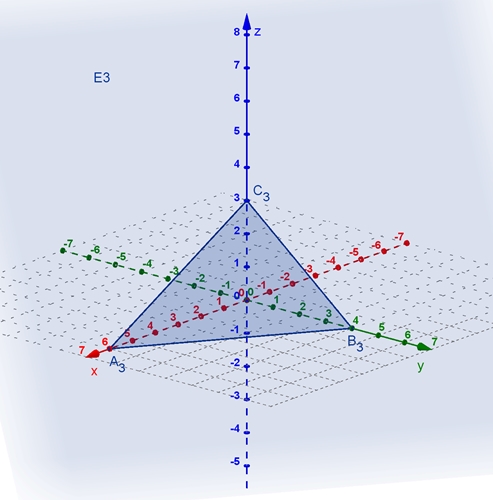
Graphische Darstellung der zugehörigen Ebenen E1, E2 und E3

Zur besseren Anschauung werden die drei Ebenen zunächst einzeln mit den Spurdreiecken dargestellt. Das Spurdreieck ist das Dreieck aus den Schnittpunkten der Ebene mit den Koordinatenachsen als Eckpunkte.

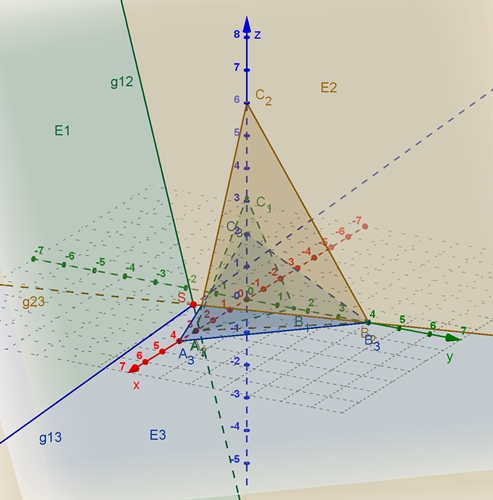
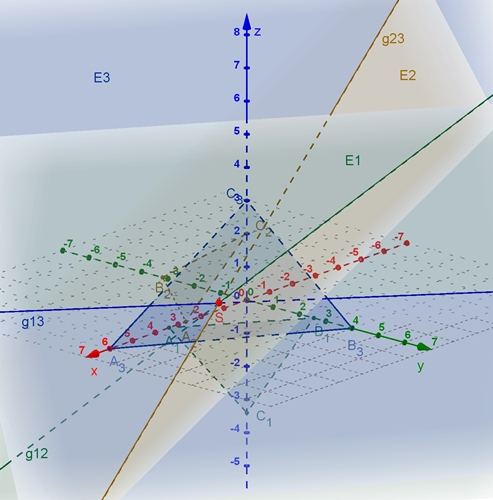
Bei der Darstellung aller drei Ebenen werden noch die Schnittgeraden der Ebenen dargestellt.

Der Schnittpunkt der Schnittgeraden und der Ebenen ist der Punkt S = (2,8; – 0,2; 0,7).

Beispiel 2:

I 3x + 4y – 3z = 10,2 | Ebene E1

II 3x – 2,5y + 4z = 8 | Ebene E2

III 2x + 3y + 4z = 12 | Ebene E3

Eine Variable reduzieren, z.B. x :

I – II = IV 3x – 3x + 4y –(–2,5y) – 3z – 4z = 10,2 – 8

3٠III – 2٠II = V 6x – 6x + 9y –(–5y) + 12z – 8z = 36 - 16

_______________________________________________

IV 6,5y – 7z = 2,2

V 14y + 4z = 20

Eine Variable reduzieren, z.B. z :

4٠IV + 7٠V 26y + 98y = 8,8 + 140

124y = 148,8

y = 1,2

Einsetzen in V :

14٠1,2 + 4z = 20

4z = 20 – 16,8

z = 0,8

Einsetzen in III:

2x + 3٠1,2 + 4٠0,8 = 12

2x = 12 – 3,6 – 3,2

2x = 5,2

x = 2,6

Lösung: (x, y, z) = (2,6; 1,2; 0,8)

Graphische Darstellung der zugehörigen Ebenen E1, E2 und E3

Bei der Darstellung aller drei Ebenen werden noch die Schnittgeraden der Ebenen dargestellt.
Der Schnittpunkt der Schnittgeraden und der Ebenen ist der Punkt S = (2,6; 1,2; 0,8).

Die 3 Ebenen können im dreidimensionalen Raum verschiedene Lagen besitzen.

Entsprechend gibt es für die 3 Gleichungen genau eine Lösung, keine Lösung oder unendlich viele Lösungen.

Graphische Darstellung von E1, E2 und E3 mit Variation der Variablen

Quadratische Gleichungen

Graphische Veranschaulichung von Beispiel 1

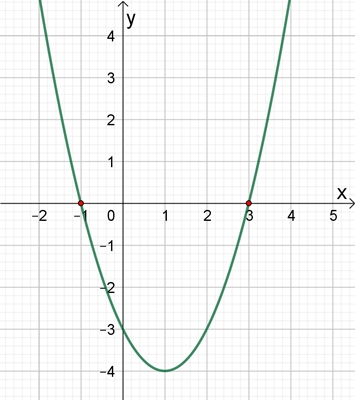
Die Lösungen x₁ = –1 und x₂ = 1,5 der quadratischen Gleichung x² – 2x – 3 = 0 (1. Beispiel) entspricht den Nullstellen der quadratischen Funktion mit der Gleichung
y = x² – 2x – 3, x є ℝ