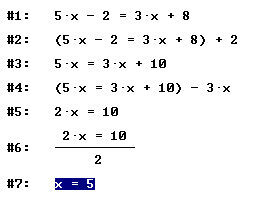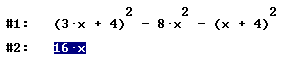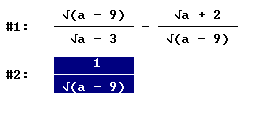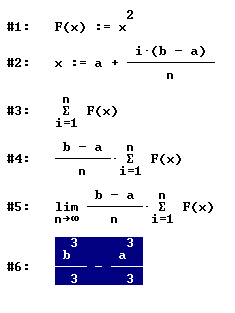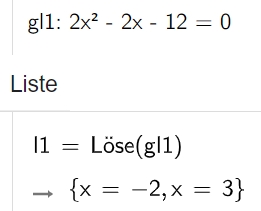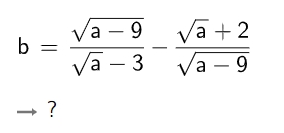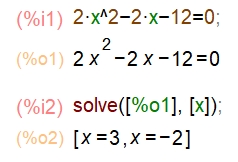Derive 5.0

Beispiele:

Schrittweises Lösen von Gleichungen:

Algebrafenster von Derive 6:                    Bemerkungen:

Mit Derive kann eine Gleichung sofort gelöst werden.
Es ist aber auch möglich die Gleichung in Schritten zu lösen:
Eingabe: 5x-2=3x+8
Eingabe: #1+2 <Enter> liefert Zeile #2
Vereinfachen Algebraisch   liefert Zeile #3.
Eingabe: #3-3x <Enter> liefert Zeile #4
Vereinfachen Algebraisch   liefert Zeile #5.
Eingabe: #5/2 <Enter> liefert Zeile #6.
Vereinfachen Algebraisch   liefert Zeile #7.
 

Algebraische Umformungen:  

Der Ausgangsterm #1 wird duch
Vereinfachen Algebraisch oder Icon =  sofort  zu Term #2 vereinfacht.
 
 

Der Ausgangsterm #1 wird duch  Vereinfachen Algebraisch oder Icon =
sofort  zu #2 vereinfacht.
Üblicherweise wird der Lösungsterm in der Schulalgebra mit rationalem
Nenner angegeben .
 
 

Schrittweiser Aufbau der Grenzwertdarstellung des bestimmten Integrals:  

Zuerst wird die Funktion F(x) definiert.
Dann wird das bestimmte Integral als Grenzwert mit Hilfe folgender Formel dargestellt:

Vereinfachen Muliplizieren von Term #5  liefert  #6.
 
 
 

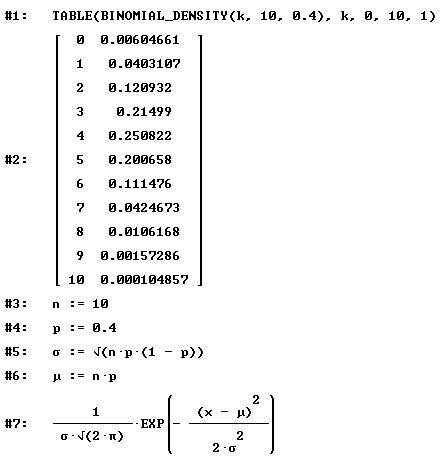
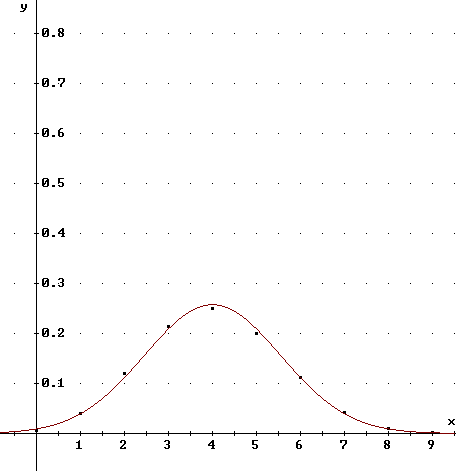
Binomial- und Normalverteilung im Vergleich

Algebrafenster von Derive 6:                                                                Grafikfenster von Derive 5:

Derive ist eines der ersten Computer-Algebra-Systeme (CAS) und ein sehr mächtiges mathematisches Hilfsmittel mit einfacher Windows-Darstellung, um alle möglichen Aufgabenstellungen zu lösen.
Es war in den Schulen weit verbreitet und hat durch den Taschencomputer TI-92, in dem Derive implementiert ist, weiter an Popularität gewonnen. Mittlerweile gibt es viele weitere Modelle.

Geogebra Classic 6.0

Seit der Version 5.0 ist ein CAS-Modul integriert.

Beispiele:

Lösen einer quadratischen Gleichung

Geogebra kann folgenden Wurzel-Term nicht vereinfachen:

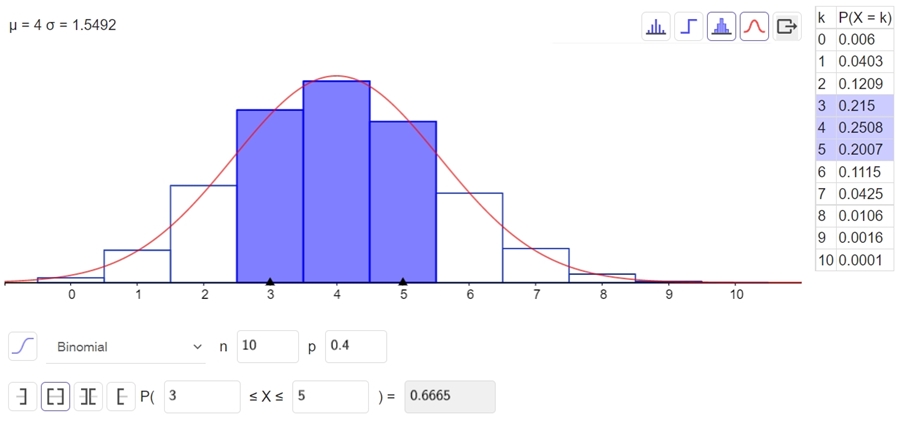
Darstellung von Binomialverteilung und Normalverteilung

im Menü Wahrscheinlichkeitsrechner ohne Angabe von Formeln

Binominalverteilung für p = 0.4, n = 10, Wahrscheinlichkeit P(3<=X<=5)

und Normalverteilung für μ = 4, σ = 1.5492

Andere Möglichkeit:

Eingabe in der Eingabezeile: Binomial( 10, 0.4)
Liefert ebenfalls die Binomialverteilung als Grafik.

Eingabe in der Eingabezeile: Binomial( 10, 0.4, 3…5)
Liefert als Ergebnis 0.66647 (Runden auf 5 Dezimalstellen)

Maxima (wxMaxima 21.05.2)

Beispiele:

Lösen einer quadratischen Gleichung

Vereinfachen eines Wurzel-Terms

Weitere Computer-Algebra-Systeme:  Mathcad, Maple, MuPAD.

Die Programme haben folgende Eigenschaften:

• wissenschaftlicher Taschenrechner mit Gleitkommazahlen und Brüchen

• Rechnen mit algebraischen Variablen, Termen, Gleichungen, Funktionen, Vektoren und Matrizen

• numerische und algebraisch-symbolische Berechnung von Ableitungen, Integralen und Grenzwerten

• Grafik mit 2D- und 3D-Darstellung