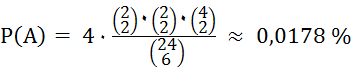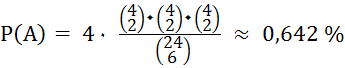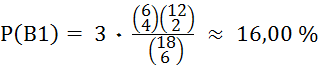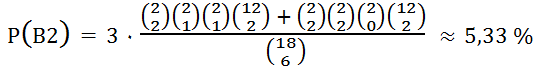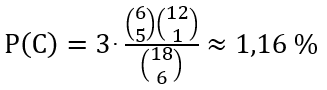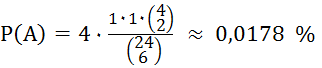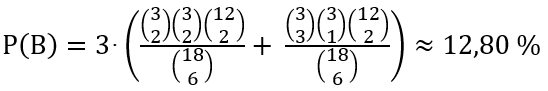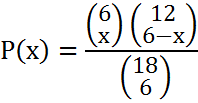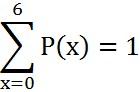Berechnung von Wahrscheinlichkeiten und relativen Häufigkeiten bei einem Solo

1.  Fall

A =   „Ein Spieler hat 2 bestimmte Ober, z.B. Eichel- und Herz-Ober, 2 bestimmte Unter, z.B. Eichel- und Herz-Unter und 2 Herz, und spielt als Ausspieler einen Herz-Solo.“

B1 =  „Ein Gegenspieler hat 4 Trümpfe.“

B2 =  „Ein Gegenspieler hat 4 Trümpfe, dabei 2 Ober, 1 oder 2 Unter.“

C =    „Ein Gegenspieler hat 5 Trümpfe.“

RH(A)    ≈   0,0171 %

RH(B1)  ≈   15,84 %,                         P(B1)  ≈   16,00 % (s. unten)   

RH(B2)  ≈   5,52 %,                           P(B2)  ≈   5,33 % (s. unten)

RH(C)    ≈   1,19 %,                           P(C)    ≈   1,16 % (s. unten)

Relative Häufigkeit RH bei 100 000 000 Spielsimulationen.

Bemerkung:

Die Wahrscheinlichkeit, den Solo in der Abbildung als Ausspieler zu gewinnen ist sehr hoch.

Falls der Ausspieler nur Herz- und Schellen-Ober hat, ist in Abhängigkeit der beiden Unter die Wahrscheinlichkeit zu gewinnen gering bis sehr gering.

2.  Fall

A =   „Ein Spieler hat 2 Ober, 2 Unter und 2 Herz, und spielt als Ausspieler einen Herz-Solo.“

B1 = „Ein Gegenspieler hat 4 Trümpfe.“

B2 = „Ein Gegenspieler hat 4 Trümpfe, dabei 2 Ober, 1 oder 2 Unter.“

C =  „Ein Gegenspieler hat 5 Trümpfe.“

RH(A)  ≈  0,640 %

RH(B1)  ≈  15,72  %

RH(B2)  ≈  5,33 %

RH(C)  ≈  1,11 %

Relative Häufigkeit RH bei 30 000 000 Spielsimulationen.

Bemerkung:

P(A) ist im 2. Fall 36-mal so groß wie im 1. Fall.

Die Wahrscheinlichkeiten für B und C sind in beiden Fällen gleich groß.

3.  Fall

A = „Ein Spieler hat Eichel-Ober, Eichel-, Herz- und Schellen-Unter und 2 Herz, und spielt als Ausspieler einen Herz-Solo.“

B = „Ein Gegenspieler hat 3 Trümpfe, dabei mindestens 1 Ober.“

C = „Ein Gegenspieler hat 4 Trümpfe, dabei mindestens 2 Ober.“

D = „Ein Gegenspieler hat 5 Trümpfe.“

RH(A) ≈   0,0177 %

P(B)   =   3  + 3  + 3   ≈  67,55 %

                     └───┬───┘           └───┬───┘          └───┬───┘

P(B) =          32,00 %    +          32,00 %      +       3,55 %       ≈  67,55 %

:  2 der 3 restlichen Trümpfe, :  3 der 12 restlichen Farbkarten,

RH(B)  ≈  67,74 %

                                                                   └─┬─┘

RH(C)  ≈   12,95 %,                 P(„3 Ober“)  ≈   3,20 %

Speziell:  P(„3 Ober“)  ≈  0,58 %

RH(D)  ≈   1,13 %

Bemerkung:

Die Wahrscheinlichkeit, den Solo als Ausspieler zu gewinnen, ist nicht sehr hoch.

Dazu Python-Programm:  RH-1O(E)-3U(EHS)-2H

Ausgabe:

Kurzer Schafkopf mit 24 Karten; 4 Spieler, 50000000 Spiele

9 = Neuner, 10 = Zehner, U = Unter, O = Ober, K = König, A = Ass

E = Eichel, G = Grün, H = Herz, S = Schellen

RH = Relative Häufigkeit

Spieler 3 :  O_S 10G U_G 10S 9_H 9_E  Anz. Trümpfe: 3

Spieler 3 :  O_G O_S K_G O_H 9_E 10E  Anz. Trümpfe: 3

Spieler 4 :  O_G O_S O_H K_G A_G K_E  Anz. Trümpfe: 3

Spieler 4 :  A_G O_H O_G O_S A_S K_E  Anz. Trümpfe: 3

Spieler 4 :  A_G K_E U_G O_G 9_S A_H  Anz. Trümpfe: 3

Spieler 2 :  O_S O_H 10G K_H A_G 10E  Anz. Trümpfe: 3

Spieler 4 :  A_S 9_G 9_S U_G O_G A_H  Anz. Trümpfe: 3

Spieler 4 :  O_S 10E A_E A_S K_H 9_H  Anz. Trümpfe: 3

Spieler 3 :  U_G A_H O_H O_S 9_S 10S  Anz. Trümpfe: 4

Spieler 4 :  10H O_G 9_H 9_G 10S O_H  Anz. Trümpfe: 4

Spieler 2 :  A_G 10H 9_E K_G O_G O_H  Anz. Trümpfe: 3

Spieler 3 :  A_H U_G K_S 10S O_S 10E  Anz. Trümpfe: 3

Spieler 2 :  U_G K_G K_H K_S O_G A_S  Anz. Trümpfe: 3

...

Es gibt 8828 -mal den Solo O(E)-U(EHS)-2H:       RH = 0.0177 %

Spieler 1 hat 2207 -mal den Solo O(E)-U(EHS)-2H.

Ein Gegenspieler hat 1495-mal 3 Trümpfe (>=1 O): RH = 67.74 %

Ein Gegenspieler hat 286-mal 4 Trümpfe (>=2 O):  RH = 12.95 %

Ein Gegenspieler hat 25-mal 5 Trümpfe:           RH =  1.13 %

Download Python-Programm RH-1O(E)-3U(EHS)-2H

mit Python Version 3.6.0

Wahrscheinlichkeitsverteilung der Anzahl x der Trümpfe eines bestimmten Gegenspielers
des Solospielers mit 6 Trümpfen

x	0	1	2	3	4	5	6
P(x) in %	4,977	25,598	39,997	23,702	5,333	0,388	0,005

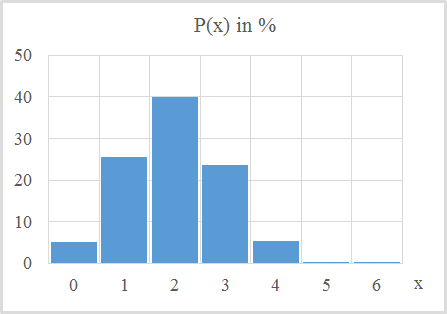x = Anzahl der Trümpfe

P(x) = Wahrscheinlichkeit eines bestimmten Gegenspielers mit x Trümpfen

  

Zurück
Zurück zur Startseite