Die
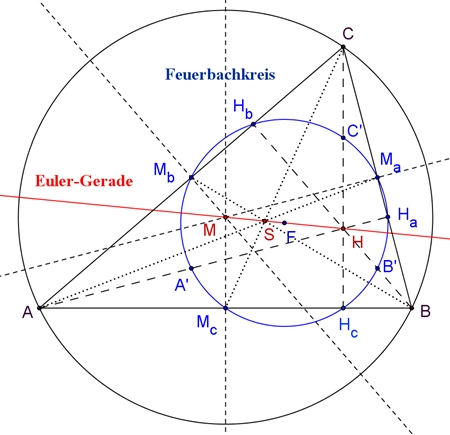
Euler-Gerade und der Feuerbachkreis.
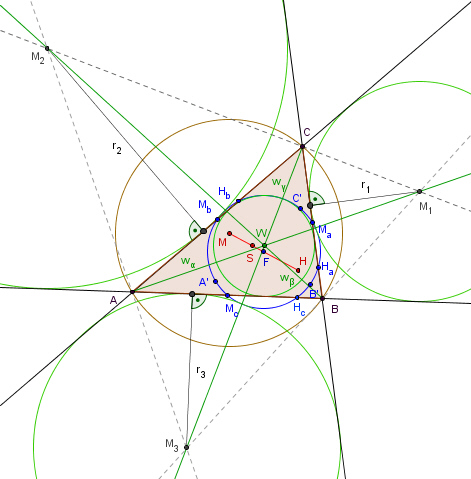
Satz über die Euler-Gerade: In jedem Dreieck
liegt der Schnittpunkt H der Höhen, der
Schnittpunkt S der Seitenhalbierenden, der Mittelpunkt des
Feuerbachkreises F
und der Schnittpunkt M der Mittelsenkrechten liegen auf einer Geraden. Diese
Gerade heißt Euler-Gerade. Satz über den Feuerbachkreis:
Die
Seitenmitten Ma, Mb, Mc und die Höhenfußpunkte
Ha, Hb, Hc eines Dreiecks und die Mittelpunkte
A’, B’, C’ zwischen den Dreiecksecken und dem Höhenschnittpunkt liegen
auf einem Kreis. Dieser Kreis heißt Feuerbachkreis oder
Neunpunktekreis.
Weitere Eigenschaften: 1. Die Euler-Gerade geht auch durch den Mittelpunkt F des Feuerbachkreises; der Mittelpunkt dieses Kreises ist gleichzeitig der Mittelpunkt der Strecke [HM]. 2. Die vier Punkte M, S, F und H sind vier harmonische Punkte mit dem Teilverhältnis | τ | = 2 : 1.
3. Im
Dreieck ABC
besitzt
der
Feuerbachkreis einen halb so
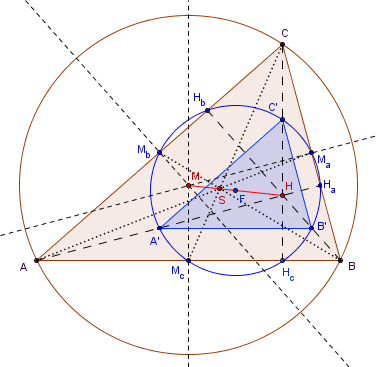
großen Radius wie der Umkreis des Dreiecks. 4. Die zentrische Streckung (H; 0,5) mit Zentrum H und Streckungsfaktor 0,5 bildet das Dreieck ABC auf das Dreieck A’B’C’ und den Umkreis des Dreiecks ABC auf den Feuerbachkreis ab.
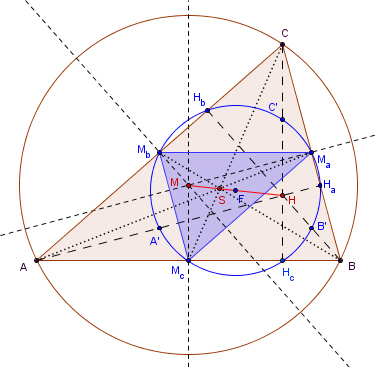
5. Die zentrische Streckung (S; -0,5) mit Zentrum S und Streckungsfaktor -0,5 bildet das Dreieck ABC auf das Dreieck MaMbMc und den Umkreis des Dreiecks ABC auf den Feuerbachkreis ab.
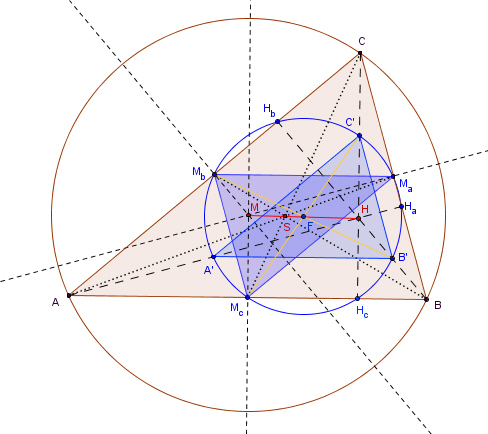
6. Die beiden zentrischen Streckungen (S;
-0,5)
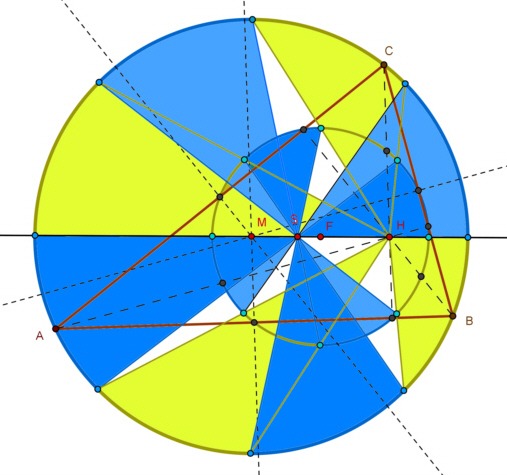
und (H; 0,5) hängen folgendermaßen zusammen: 7. Beim gleichseitigen Dreieck wird der Neunpunktekreis zum Inkreis des Dreiecks. 8. Der Neunpunktekreis wird vom Inkreis und von den drei Ankreisen des Dreiecks ABC berührt.
Folgendes Bild entstand nach Vorlage eines Bildes in der Zeitschrift
PM Oktober
2007, S. 49.
Sämtliche Konstruktionen wurden mit Hilfe von geogebra durchgeführt. Quellen für Beweise: http://lsgm.uni-leipzig.de/KoSemNet/pdf/graebe-99-1.pdf
http://www.zum.de/Faecher/Materialien/rubin/texte/DreiGeom.pdf |