Die Violine oder Geige, der goldene Schnitt,

Konstruktion der Form einer Violine

und das Apfelmännchen

Beim goldenen Schnitt gilt:

Der längere Streckenabschnitt ist ungefähr 61,8% der gesamten Streckenlänge oder
der kürzere Streckenabschnitt ist ungefähr 61,8% des längeren Streckenabschnitts.

   

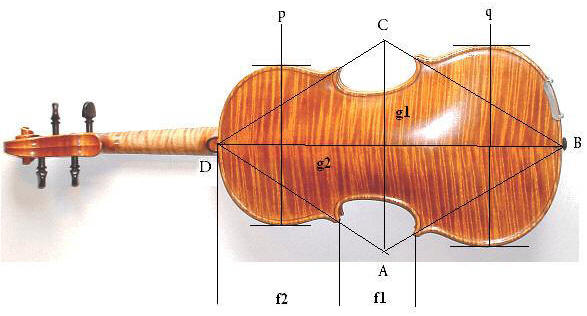
Oberseite Violine (Geigenbauer Johann Goldfuß, Baujahr 1969), Fotos M. Holzapfel:  

    

 d1 : d2  ≈  0,614,  e1 : e2  ≈  0,628

 

  Unterseite Violine:  

Unterseite Goldfuß-Geige 

f1 : f2  ≈  0,614,  g1 : g2  ≈  0,614,  d(p;q) : d(B;D)  ≈  0,607

g1 = d(A;C),  g2 = d(B;D)

d(p;q) = Abstand der Geraden p von der Geraden q

Vergleich mit der näherungsweisen Konstruktion weiter unten.

  Die Proportionen der Violine haben sich im Verlauf der Geschichte mehrfach verändert. Der goldene Schnitt hat sich als günstiges Konstruktionsprinzip erwiesen. Dies hat nicht nur ästhetische sondern wahrscheinlich auch physikalische Gründe: Durch ein irrationales Verhältnis (in Näherung: Verhältnis zweier größerer benachbarter Zahlen in der Fibonacci-Folge) bei den Proportionen der Violine können besonders starke Resonanzeffekte des Geigenkörpers bei einzelnen Tönen reduziert werden. Mit Hilfe anderer konstruktiver Methoden beim Geigenbau ergibt sich dann ein ausgewogener Klang der Geige im gesamten Klangbereich.

 

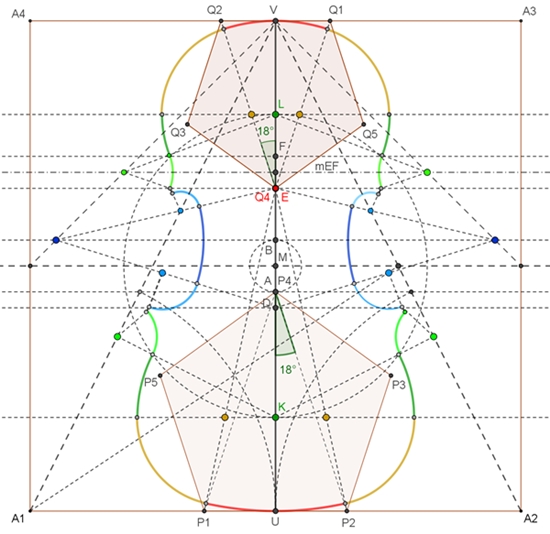
Näherungsweise Konstruktion der Form einer Violine

Mit folgenden Annahmen wurde die Konstruktion mit Hilfe von Geogebra durchgeführt:

A1A2A3A4 ist ein Quadrat,
 U ist der Mittelpunkt der Strecke A1A2, V ist Mittelpunkt der Strecke A3A4,
M ist der Mittelpunkt der Strecke UV.

σ ≈ 0,618  ist goldene Schnittzahl.

P1P2P3P4P5 und Q1Q2Q3Q4Q5 sind jeweils reguläre Fünfecke.

Die Spitze des Fünfecks P4 habe ich im Punkt A gewählt, wobei die Seite P1P2 auf A1A2 liegen soll. Beim regulären Fünfeck gilt:  ≮ P1P4P2 = 36°. Den Punkt P2 erhält man als Schnittpunkt von A1A2 mit dem freien Schenkel des Winkels 18° an Strecke UA im Punkt A. Die Punkte P3 und P5 werden eigentlich nicht benötigt und sind nur der Vollständigkeit halber dargestellt.

Entsprechende Konstruktion für Q2.

Ich habe zunächst versucht den Punkt D als Spitze P4 des Fünfecks zu wählen. Die Konstruktion liefert dann aber keine so gute Deckungsgleichheit mit der Stradivari-Geige.

Die weiteren Konstruktionen sind achsensymmetrisch zur Achse UV.

Die einzelnen Bogen mit Bogenmittelpunkten sind mit gleicher Farbe gekennzeichnet.

    

Konstruktion der Form einer Violine mit Hilfe von Geogebra

 
Konstruktion durch M. Holzapfel

   

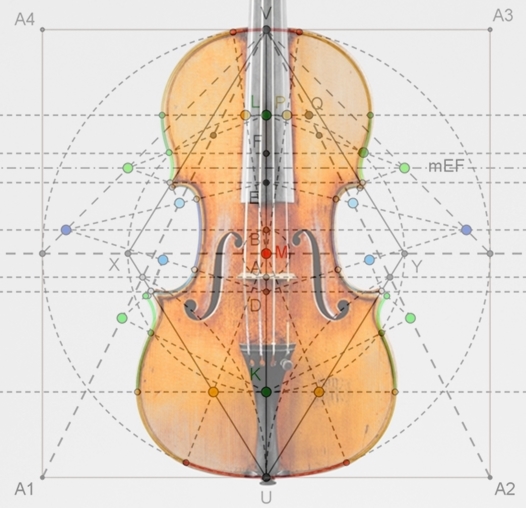
Überlagerung der Konstruktion mit der Violine "Antonius 1711" von Stradivari

 

Als Vorlage für die Oberseite der Violine von Antonio Stradivari wurde das Bild „Antonius (1711)“ von Wikipedia verwendet:

https://de.wikipedia.org/wiki/Antonio_Stradivari

 

                               Überlagerung der Konstruktion mit einer Violine von Andrea Amati von ca. 1570

  

 Vorlage für die Oberseite der Violine
 

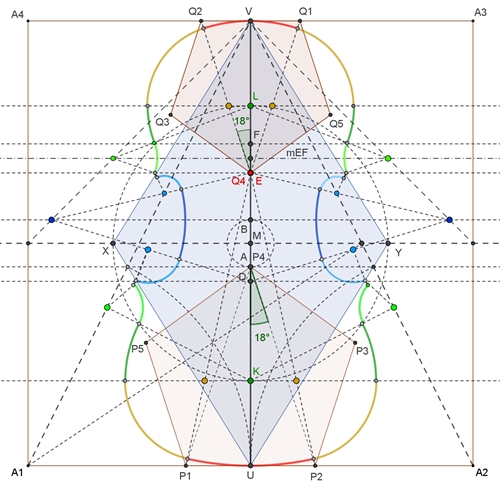
Vergleich der Messwerte in obiger Goldfuß-Violine mit der Konstruktion

d(X;Y) : d(U;V)  =  σ

d(K;L) : d(U;V)  =  σ

d(V;D) : d(V;U)  =  σ

σ ≈ 0,618

Hinweis:

https://www.schiele-geigenbau.de/docs/Schiele_Artikel_GoldenerSchnitt.pdf

 

Das Apfelmännchen und der goldene Schnitt?

  Die Mandelbrotmenge wird im deutschen Sprachbereich wegen seiner Form oft als Apfelmännchen bezeichnet. Mathematiker sehen im Apfelmännchen eine Figur, in der sich mathematische Zusammenhänge veranschaulichen lassen und die ein Sinnbild für die Chaostheorie und für die Geometrie der Fraktale darstellt..

  Im Apfelmännchen können die Knospen (Ausbuchtungen) den Fibonacci-Zahlen zugeordnet werden. 

 

d1 : d2  ≈  0,63

Goldener Schnitt?  Nicht exakt! Aber in Näherung!

  

Apfelmännchen und Violine

   

  

Zurück
Zurück zur Startseite