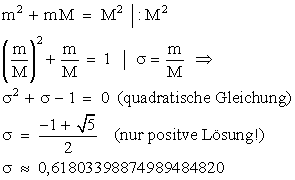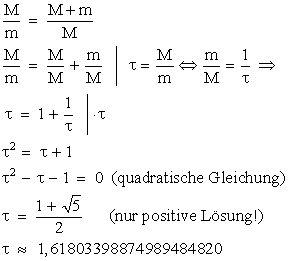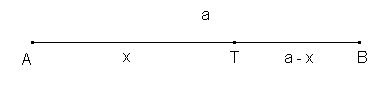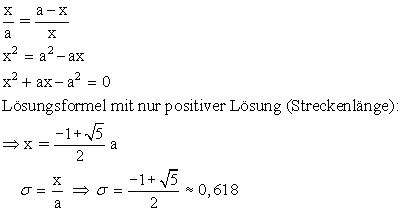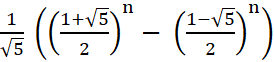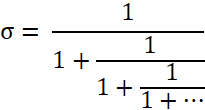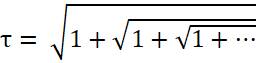Goldener Schnitt – Eigenschaften

Beim goldenen Schnitt bzw. bei der stetigen Teilung handelt es sich um ein besonderes Teilungsverhältnis, wobei aus geschichtlichen Gründen für die längere Teilstrecke die Bezeichnung Major (M) und für die kürzere Teilstrecke die Bezeichnung minor (m) bzw. Minor üblich ist.

Mit diesen Bezeichnungen lässt sich die Bedingung für den goldenen Schnitt wie folgt angeben:

               m  :  M  =  M  :  (M+m)      

Der kürze verhält sich zum längeren Streckenabschnitt wie der längere Streckenabschnitt zur gesamten Streckenlänge.

              

Lösung für die linke Gleichung des goldenen Schnitts:

Lösung für die rechte Gleichung des goldenen Schnitts:

Lösung mit Hilfe der Lösungsvariablen x  für die Streckenlänge von [AT]  bei gegebener Streckenlänge a von [AB]:

Bemerkungen:  

σ (sigma) und  τ (tau)  werden auch goldene Schnittzahlen genannt.

An Stelle von τ wird auch Φ (Phi) verwendet.

Beim goldenen Schnitt hat der längere Streckenabschnitt etwa 61,8% der gesamten Streckenlänge.

Fibonacci-Folge und der goldene Schnitt

Fibonacci-Folge:  1, 1, 2, 3, 5, 8 ,13, 21, 34, 55, 89, 144, 233, ...

Die Formel für die Fibonacci-Folge lautet:

Fn+2  = Fn+1  +  Fn   mit F1 = 1 und F2 = 1

Quotienten zweier aufeinanderfolgender Fibonacci-Zahlen:

Formel von Moivre-Binet  (1843):   Fn =

Für n = 1, 2, 3, 4 ,5, …  ist  Fn = 1, 1, 2, 3, 5, …

Mit Hilfe der Formel von Moivre-Binet  lässt sich zeigen, dass die Quotienten zweier aufeinanderfolgender Fibonacci-Zahlen gegen s gehen:

,  da  

Daraus folgt:  

Eigenschaften der goldenen Schnittzahlen s  und  t

1) 

2)    (2)

3)  Aus (2)٠τ folgt:

τ2 = τ + 1  |  ٠τn

τn+2 = τn+1 + τn

Damit ergeben sich folgende Potenzen von τ:

τ1  = τ

τ2 = τ1 + τ0  = τ + 1

τ3 = τ2 + τ1  = 2τ + 1

τ4 = τ3 + τ2  = 3τ + 2

τ5 = τ4 + τ3  = 5τ + 3

τ6 = τ5 + τ4  = 8τ + 5

…           

Die höheren Potenzen von t haben die Struktur der Fibonacci-Folge:

1, 1, 2, 3, 5, 8 ,13, 21, 34, 55, 89, 144, 233, ...

4)  σ lässt sich als Kettenbruch darstellen:

                                                                              

Der Wert des Kettenbruchs kann durch die Rekursion  xi+1 = 1 / (1 + xi)  ermittelt werden.
Falls es einen Grenzwert gibt, müssten sich xi+1 und xi diesem immer mehr annähern, d.h. es gilt dann:

x = 1 / (1+x)  ⇔  x2 + x – 1 = 0

Die positive Lösung dieser Gleichung ist  σ = (  – 1) / 2

5)  

Der Wert der ineinander geschachtelten Wurzeln lässt sich mit Hilfe der Rekursion 

bestimmen. Falls es einen Grenzwert x gibt, müssten sich xi+1 und xi diesem immer mehr annähern, d.h. es gilt dann

   ⇔   x2 = 1 + x   ⇔   x2 – x – 1 = 0

Die positive Lösung für diese Gleichung ist  τ = (  + 1) / 2

Zurück
Zurück zur Startseite