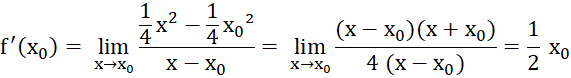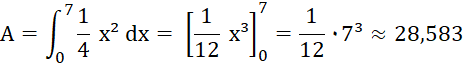Ableitung – Steigung

Beispiel:  f(x) = ¼ x², x ϵ ℝ

Graphische Darstellung

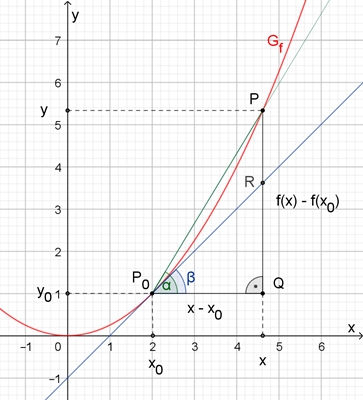
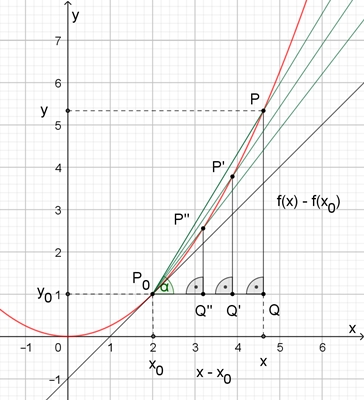  Animierte Darstellung

Bezeichnungen:

Das Dreieck P0QP heißt Steigungsdreieck.

  heißt Differenzenquotient und gibt die Steigung m = tan α der Sekante [P0P] an.

Falls der Grenzwert  existiert, heißt er Differentialquotient und gibt die Steigung m = tan β  der Tangente an den Graphen Gf im Punkt P0 an.

Der Differentialquotient wird als Ableitung f‘(x0) der Funktion f an der Stelle x0 bezeichnet.

Im Beispiel:

Für x0 = 2 ergibt sich die Steigung f‘(2) = 1 mit β = 45°.

Ableitungsregel für eine Potenzfunktion f mit der Konstanten c:

f(x) = c٠xn  ⇒ f‘(x) = c٠n٠xn-1  z.B   f(x) = ¼ x²  ⇒ f‘(x) = ½ x

 

Anwendung in der Physik

Eine Kugel rollt eine schiefe Ebene herunter. Die Kugel erfährt wegen der auf sie wirkenden Gewichtskraft eine beschleunigte Bewegung.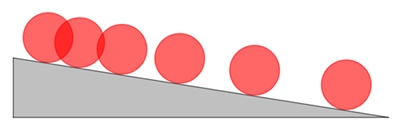


Der zurückgelegte Weg s in Abhängigkeit von der Zeit t sei durch folgende Funktion beschrieben:

s(t) = ¼ t², s in dm, t in s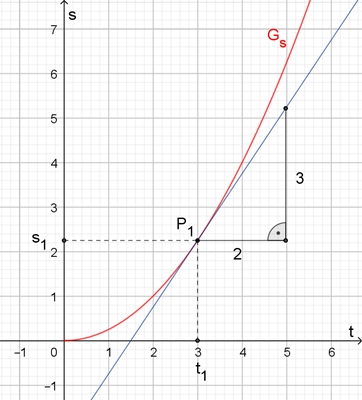

Grafische Darstellung
 

  

Zum Zeitpunkt t1 = 3 s hat die Kugel 9/4 dm = 22,5 cm zurückgelegt.

Ihre Geschwindigkeit v zu einem beliebigem Zeitpunkt t  ist die Ableitung von s nach der Zeit t
s‘(t) = ½ t 

Ihre Geschwindigkeit v zum Zeitpunkt t1 = 3 s ist dann 
s‘(3) = ½٠3 = 1,5

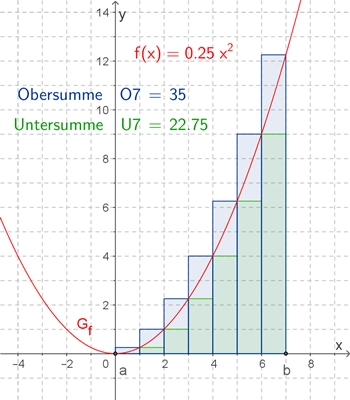
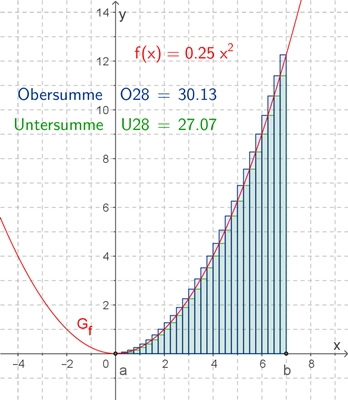
Mit Einheiten:  v = 1,5 dm/s = 15 cm/s



 
 
 
 

Integral – Flächeninhalt


 Beispiel:  f(x) = ¼ x², x ϵ ℝ

Um den Flächeninhalt unter dem Graphen Gf über dem Intervall [0;7] näherungsweise zu bestimmen, werden Rechtecke gleicher Breite wie folgt einbeschrieben, wobei der Flächeninhalt bei der Obersumme von oben, bei der Untersumme von unten angenähert wird.

Graphische Darstellung von Unter- und Obersummen
 
       Darstellung animiert

Definition

Die Funktion f mit f(x) ≥ 0 sei im Intervall [a, b] definiert.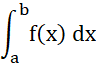
Dann nennt man den gemeinsamen Grenzwert von Unter und Obersumme das Integral der Funktion f zwischen den Grenzen a und b,  i.Z.
                                                                           

 

Zusammenhang zwischen Ableitung und Integration

Hauptsatz der Differential- und Integralrechnung (HDI)

Die Funktion f: t ⟼ f(t) sei im Intervall [a;b] definiert.
Dann gilt für die Integralfunktion  Ia: x ⟼ :

                           Ia‘(x) = f(x)  für x ϵ [a;b].    

Eine Funktion F: x ⟼ F(x)  mit der Eigenschaft F‘(x) =  f(x) heißt Stammfunktion von f.

Damit gilt:  Ia(x)  =  F(x) + c,  c = Konstante.
Verwendung der Stammfunktion bei der Berechnung von Integralen:

                         

 
Beispiel einer Integralfunktion als Potenzfunktion

Ia(x) = 1/12 x³

Ia‘(x) = f(x) = 1/4 x²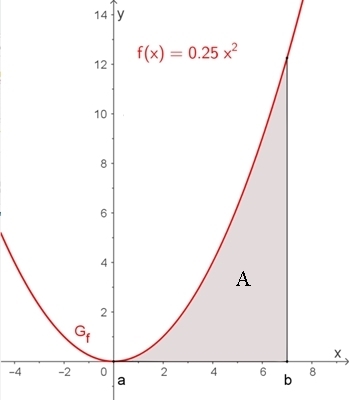


 
 
 
 

Anschaulich stellt das Integral von f(x) dx von 0 bis 7 die Maßzahl des Flächeninhalts A zwischen dem Graphen Gf der x-Achse und den Grenzen a = 0 und b = 7 dar:


 
 
 
 
 
  
  
 

 
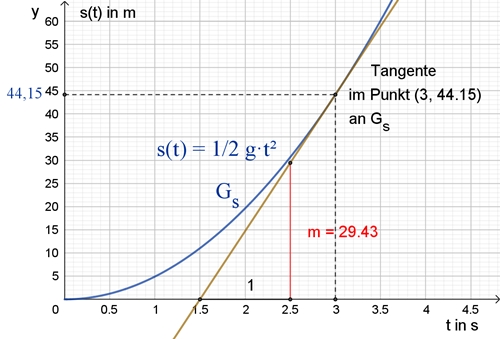
Beispiel aus der Physik, freier Fall

Beim freien Fall mit der Erdbeschleunigung g = 9,81 m/s² und ohne Berücksichtigung der Luftreibung gilt
für die gefallene Strecke s(t) (in Meter m) zum Zeitpunkt t (in Sekunden s) mit s(0) = 0:
                                             s(t) = ½ g t²

für die Geschwindigkeit v zum Zeitpunkt t, Anfangsgeschwindigkeit zum Zeitpunkt t = 0 s sei v = 0 m/s: 
                                             v(t) = g t

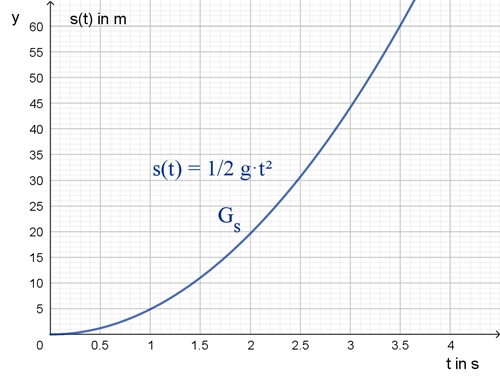
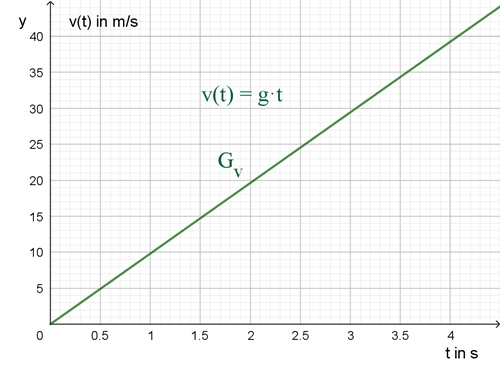Graphische Darstellung von s(t) und v(t)

 

Es gilt:  

v(t) ist die Ableitung von s(t) nach t:           

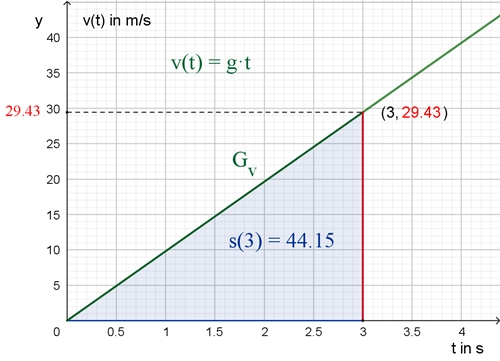
s(t) ist das Integral von v(t)  von 0 bis t:   

Graphische Darstellung des Zusammenhangs zwischen s(t) und v(t) für t = 3 s

 

           s(3 s) = ½٠9,81 m/s²٠3² s² ≈ 44,15 m,                          v(3 s) = 9,81 m/s²٠3 s ≈ 29,43 m/s

Zurück
Zurück zur Startseite