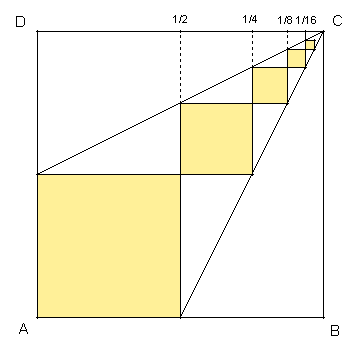
Quadrate im Quadrat - Grenzwert

Einem Quadrat der Seitenlänge 1 (Einheitsquadrat) werden Quadrate folgendermaßen einbeschrieben:

Wie groß ist die Summe der Flächeninhalte aller einbeschriebenen Quadrate?

Lösungen:

1. Weg (anschaulich geometrisch):

Die einzelnen Quadrate entstehen jeweils durch zentrische Streckung mit dem Zentrum C und dem Streckungsfaktor ½ aus dem linken unteren Quadrat der Seitenlänge ½ .

Die Seitenlängen der Quadrate sind  dann      und die Flächeninhalte  .

Die Summe der Flächeninhalte der Quadrate innerhalb des Vierecks AM_aCM_d wird durch folgende unendliche Reihe dargestellt:
                                                                                          

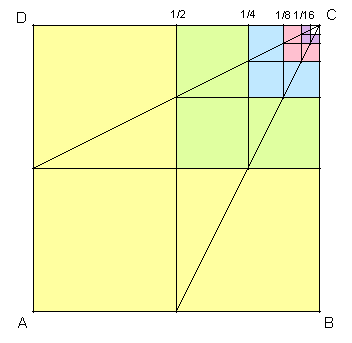
Die jeweils rechts und oben anliegenden Quadrate bilden mit dem mittleren Quadrat jeweils drei gleich große Quadrate in L-Form. Die Flächen aller L-Formen zusammen ergeben die Fläche des Einheitsquadrats. 
Daraus folgt:
                          
   

2. Weg (mit geometrischer Reihe):

Die Summe der Flächeninhalte der Quadrate innerhalb des Vierecks AM_aCM_d wird durch folgende geometrische Reihe dargestellt:

     (1)

Formel für die geometrische Reihe:

Für  |q| < 1 gilt      und damit  

Zurück
Zurück zur Startseite