Parkette mit 5-facher Rotationssymmetrie, Achsensymmetrie, 
Penrose-Parkett und Spiral-Parkette

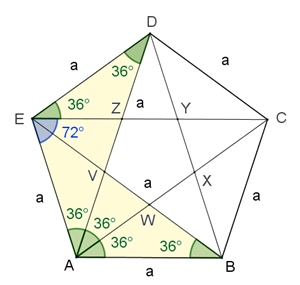
Das regelmäßige Fünfeck hat eine 5-fache Rotationssymmetrie und besitzt 5 Symmetrieachsen.

Es ist eine geometrische Figur mit folgenden weiteren Eigenschaften:

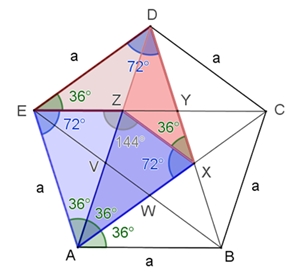
1.  Alle Seiten a und alle Diagonalen d sind gleich lang.

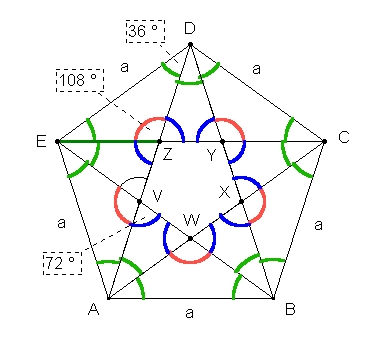
2. Die grün gekennzeichneten Winkel sind 36°. Die übrigen Winkel sind entweder doppelt so groß, 72°  (blau gekennzeichnet) oder dreimal so groß, 108° (rot gekennzeichnet).

3. Diagonale d und Seite a stehen im Verhältnis des goldenen Schnitts:      .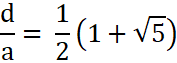 
Deshalb enthält das regelmäßige Fünfeck spitze und stumpfe goldene Dreiecke.

4. Ebenso wie das Fünfeck ABCDE ist das Fünfeck VWXYZ regelmäßig. Dieser Vorgang kann rekursiv fortgesetzt werden.

5. Der Abbildungsmaßstab m der Ähnlichkeitsabbildung, die das regelmäßige Fünfeck ABCDE in das regelmäßige Fünfeck VWXYZ abbildet:     

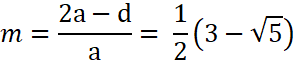
6. Im regelmäßigen Fünfeck befinden sich die Teilfiguren, die die Ausgangsfiguren einer Penrose-Parkettierung darstellen.

Penrose-Parkettierungen

Die Penrose-Parkettierung ist nach dem britischen Physiker Robert Penrose benannt, welcher 1974 entdeckte, dass man mit folgenden kleinen und großen Rauten eine Fläche vollständig bedecken kann, ohne dass das Parkett symmetrisch ist oder sich periodisch wiederholt.

Die Rauten einer Penrose-Parkettierung kommen in einem regelmäßigen Fünfeck vor.

1) Parkettierungen mit Kite und Dart

Kite (konvexer Drachen AXZE) und Dart (Pfeil = konkaver Drachen EZXD).

Das Verhältnis zweier unterschiedlich langer Seiten ist durch den goldenen Schnitt gegeben. Beide Figuren zusammen ergeben eine Raute.

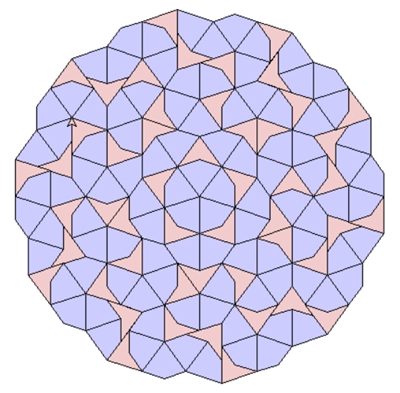
Fünffache Rotationssymmetrie einer Parkettierung aus Kites und Darts mit 5 Kites:
a) Im Ursprung „Sonne“ mit 5 Kites             b) Im Ursprung „Stern“ mit 5 Darts

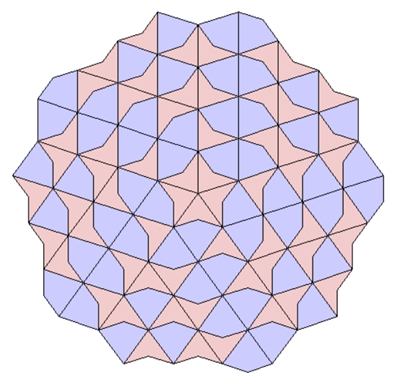
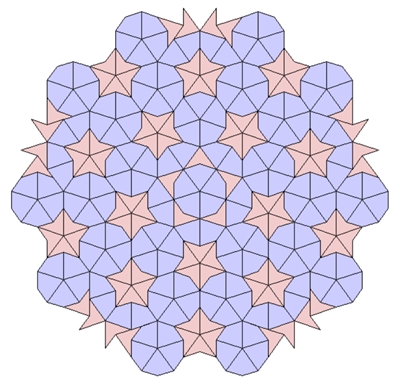
Fünffache Rotations- und Achsensymmetrie einer Parkettierung aus Kites und Darts:
a) Im Ursprung „Sonne“ mit 5 Kites              b) Im Ursprung „Stern“ mit 5 Darts

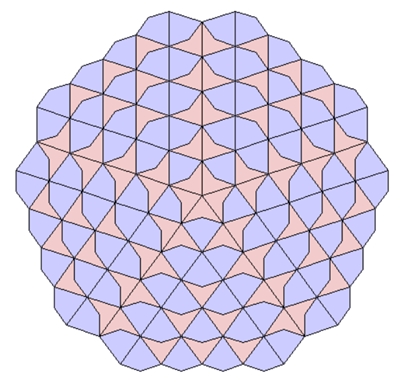
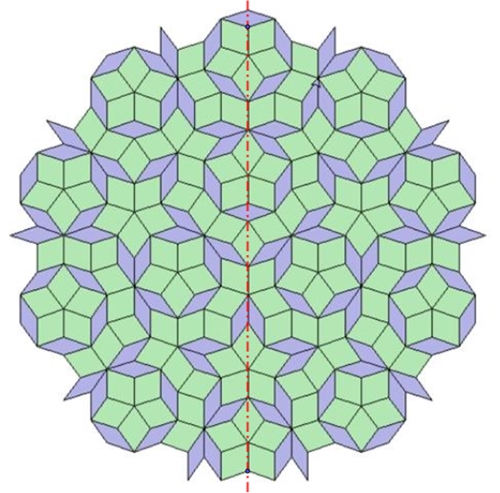
Eine versteckt periodische Parkettierung aus Kites und Darts mit einer senkrechten Symmetrieachse durch den Ursprung:

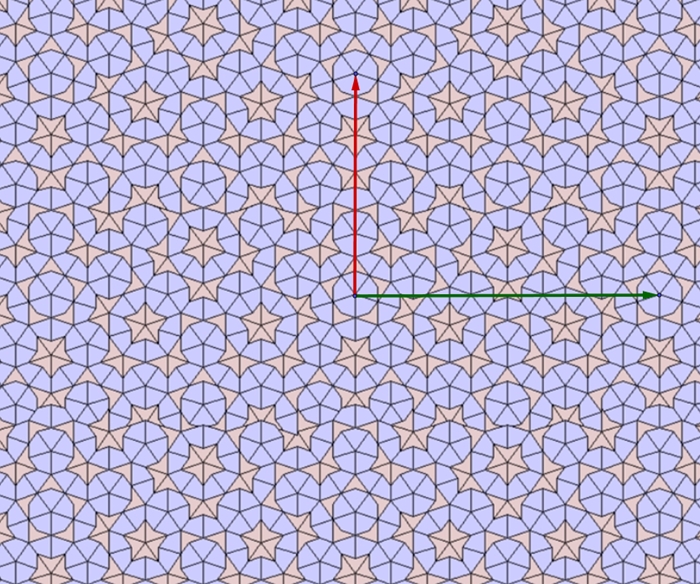
Sowohl eine Verschiebung in horizontaler x-Richtung wie auch in vertikaler y-Richtung liefert eine Wiederholung des Musters.

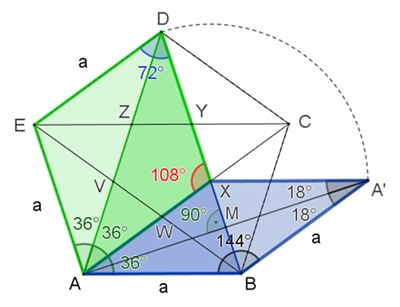
2) Parkettierungen mit großer und kleiner Raute

Große Raute AXDE und kleine Raute ABA'X. Alle Seiten sind gleich lang.

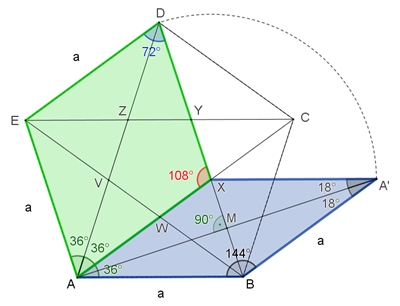
Fünffache Rotations- und Achsensymmetrie einer Parkettierung aus großen und kleinen Rauten:
a) Im Ursprung 5 große Rauten                    

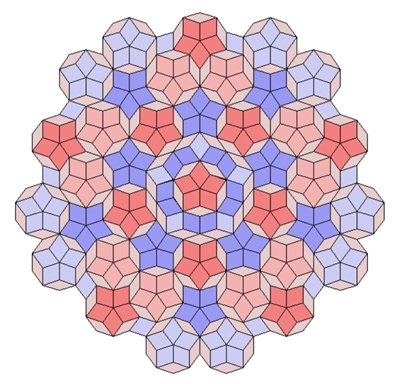
b) Im Ursprung 10 kleine Rauten

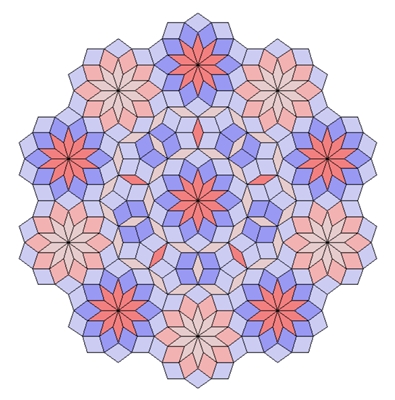                                            Mit nur einer Symmetrieachse

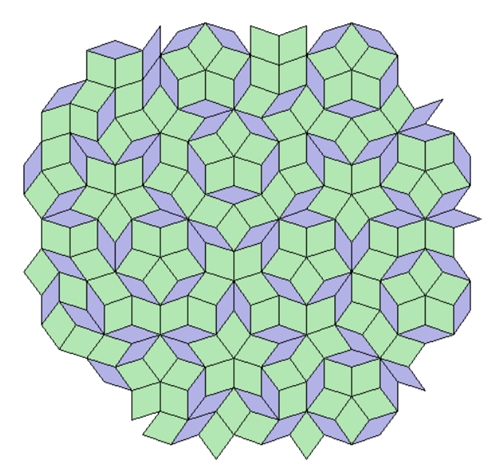
                 Penrose-Parkettierung, nicht-periodisch und nicht-symmetrisch

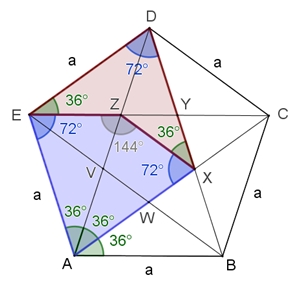
3) Parkette mit regulären Fünf- und Zehnecken

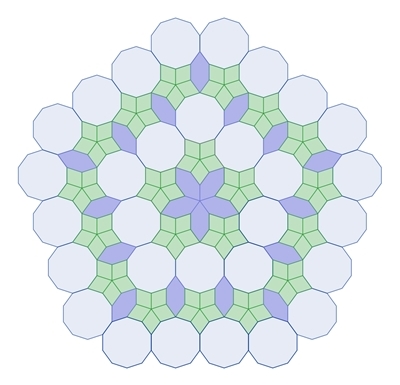
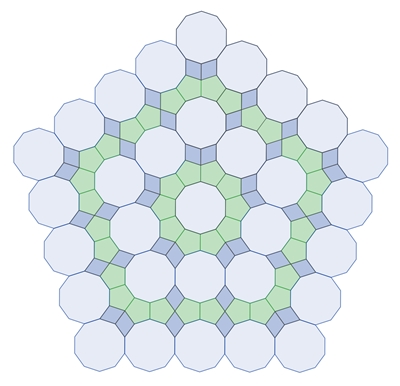
Mit Hilfe eines gleichseitigen Sechsecks mit den Innenwinkeln zweimal 72° und viermal 144°  (Innenwinkelsumme 720°) oder einer großen Raute mit den Innenwinkeln zweimal 72° und zweimal 108° (Innenwinkelsumme 360°) kann die Ebene mit regulären Fünf- und Zehnecken parkettiert werden.

4) Parkettierungen mit goldenen Dreiecken

a) Parkettierungen mit goldenen Dreiecken als Hälften von Kites und Darts

Großes goldenes Dreieck XZA und kleines goldenes Dreieck XDZ. Die Seitenlängen der goldenen Dreiecke stehen im Verhältnis des goldenen Schnitts.

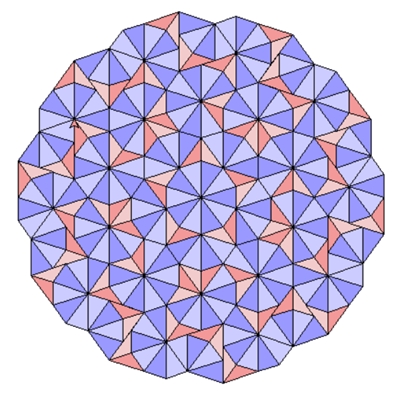
Parkettierungen unter 1a und 1b mit goldenen Dreiecken

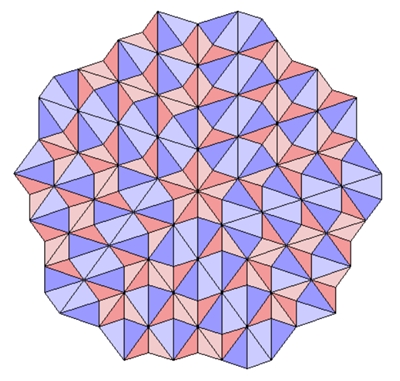
b) Parkettierungen mit goldenen Dreiecken als Hälften von kleiner und großer Raute

Goldene Dreiecke DAX und BXA.

Parkettierungen unter 2a und 2b mit goldenen Dreiecken

5) Spiralförmige, nicht-periodische und nicht-symmetrische Parkette 

a) Spiralförmige Parkettierungen mit goldenen Dreiecken 

                                Parkettierung mit spitzen goldenen Dreiecken

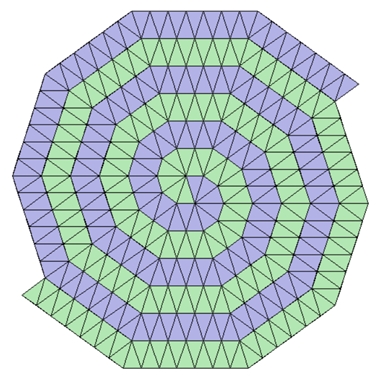                                      Farblos: Rotationssymmetrie

Parkettierung mit spitzen goldenen Dreiecken und mit einem stumpfen goldenen Dreieck (rot)

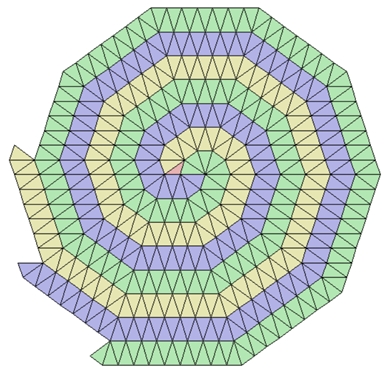
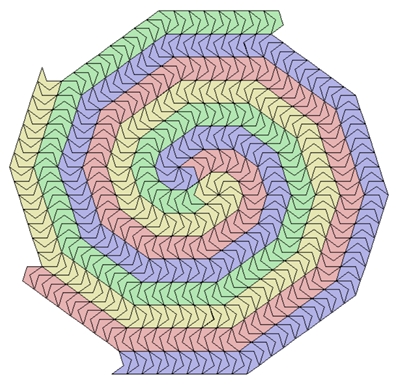
b) Spiralförmige Parkettierung mit der Krone

Die Krone ist das konkave Fünfeck ABVDE mit gleich langen Seiten.

                                        Parkettierung mit der Krone

Bereits auf islamischen Ornamenten (z.B. Darb-i-Imam-Schrein von 1453, Isfahan, Iran) tauchen Penrose-Parkettierungen auf.

Literatur- und Quellenangabe:

 https://de.wikipedia.org/wiki/Penrose-Parkettierung