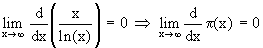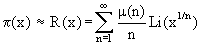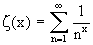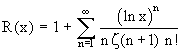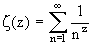Anzahl von PrimzahlenEine
Primzahl p ist eine
natürliche Zahl größer als 1 , Die Primzahlen bis 1000:
2
3 5
7 11 13
17 19
23 29 31
37 41
43 47 53
59 61
67 71 73
79 83
89 97 101 103 107 109 113 127 131 137 139 149 151 157 163
167 173 179 181 191 193 197 199 211 223
227 229 233 239 241 251 257 263 269 271
277 281 283 293 307 311 313 317 331 337
347 349 353 359 367 373 379 383 389 397
401 409 419 421 431 433 439 443 449 457
461 463 467 479 487 491 499 503 509 521
523 541 547 557 563 569 571 577 587 593
599 601 607 613 617 619 631 641 643 647
653 659 661 673 677 683 691 701 709 719
727 733 739 743 751 757 761 769 773 787
797 809 811 821 823 827 829 839 853 857
859 863 877 881 883 887 907 911 919 929
937 941 947 953 967 971 977 983 991 997 Bereits um 300 v. Chr. hat Euklid bewiesen, dass es unendlich viele Primzahlen gibt und dass jede natürliche Zahl entweder eine Primzahl ist oder als Produkt von Primzahlen dargestellt werden kann. Primzahlfunktion p(x) = Anzahl aller Primzahlen, die kleiner oder gleich der natürlichen Zahl x ist. Tabelle:
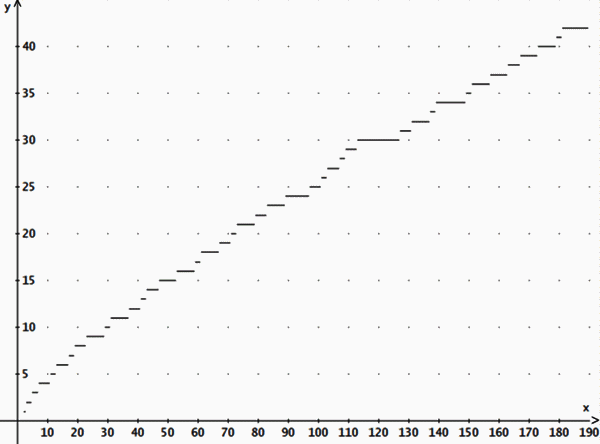
Beispiel: p(11) = 5, p(1000) = 168 Der Graph von p(x) ist eine Treppenfunktion:
Die Frage, ob sich p(x) durch eine mathematische Funktion nähern lässt, beschäftigt Mathematiker seit über 200 Jahren.
Definition: Zwei Funktionen f(x) und g(x) heißen
asymptotisch gleich, falls
Schreibweise:
Näherung durch Carl Friedrich Gauß (1792):
Bessere Näherung durch C. F. Gauß (1849):
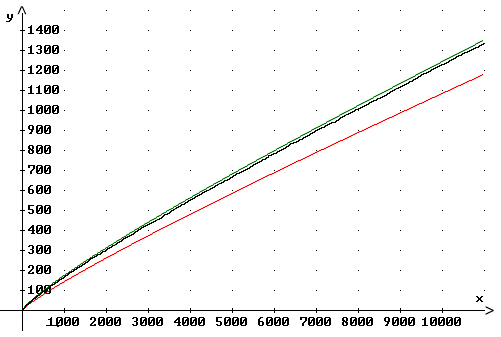
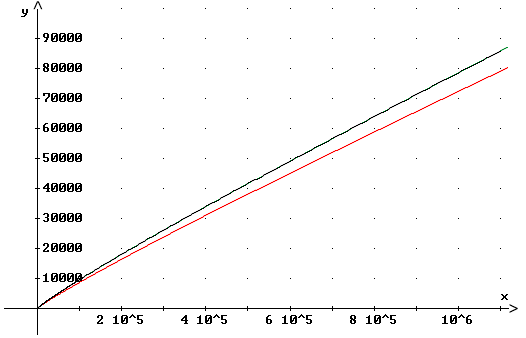
In der graphischen Darstellung wird für große x der Unterschied zwischen den Graphen von Li(x) (grün) und p(x) (schwarz) immer geringer. Abschätzung durch Tschebyscheff (1850):
Primzahlsatz von Hadamard und de la Vallée-Poussin (1896) : Folgerungen:
Der Graph von p(x) geht für x gegen unendlich gegen unendlich, wird aber immer flacher. Eine noch bessere Näherung
lieferte Bernhard Riemann (1859) mit der Riemannschen R-Funktion und der Möbiusfunktion μ(n):
Riemannsche Zetafunktion:
Andere Schreibweise mit Hilfe der Zetafunktion:
Vergleich der Genauigkeit von Li(x) und R(x) im Vergleich zu p(x)
1) Auf Einer gerundet Bemerkung: Riemann hat die Zetafunktion auf komplexe Argumente z verallgemeinert.
Dabei ist er auf Eigenschaften der
komplexen Funktion gestoßen, die eine Korrektur des Fehlers bei der Näherung von
π Bei der Untersuchung der Nullstellen der komplexen Zetafunktion hat er vermutet, dass die Zetafunktion außer den reellen Nullstellen nur auf der Geraden: Realteil(z) = 0,5 weitere unendlich viele Nullstellen besitzt. Diese sogenannte Riemannsche Vermutung spielt in der Zahlentheorie eine große Rolle, konnte aber bisher noch nicht bewiesen werden. Für den richtigen Beweis wurde 1 Million $ gestiftet. Buchempfehlung: Marcus du Sautoy: Die Musik der Primzahlen Auf den Spuren des größten Rätsels der Mathematik
Zurück Zurück zur Startseite |
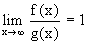
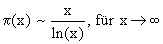
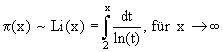 (Graph grün)
(Graph grün)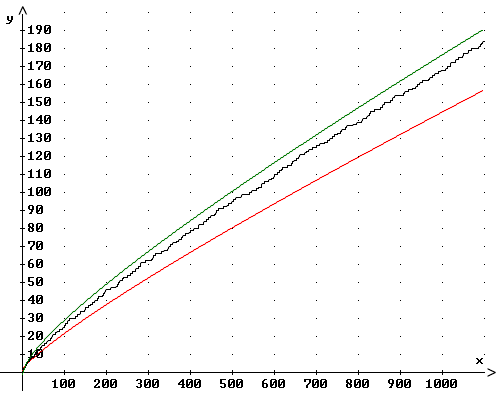
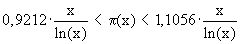
 ,
,