|
Sierpinski-Dreieck Entstehung des Sierpinski-Dreiecks
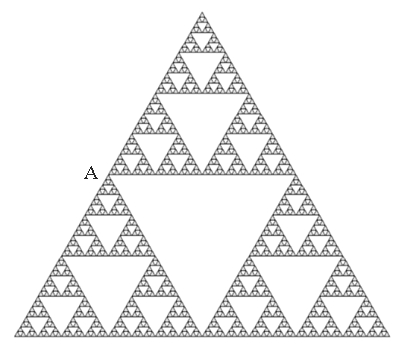
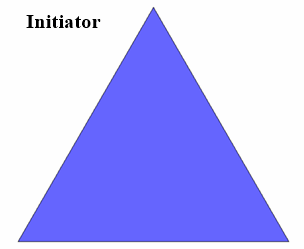
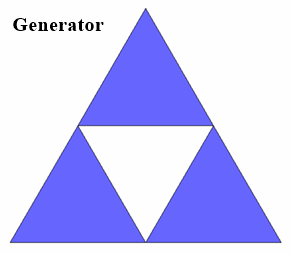
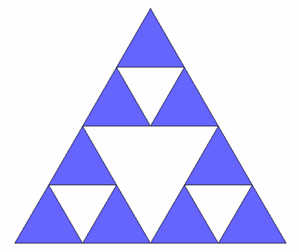
Das Sierpinksi-Dreieck ist nach dem polnischen Mathematiker Waclaw Sierpinski (1882-1969) benannt. Es entsteht folgendermaßen:
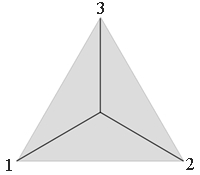
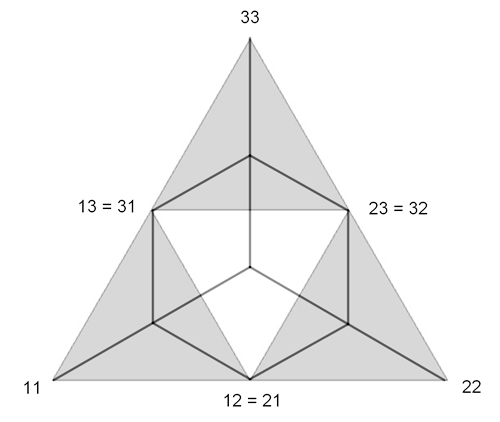
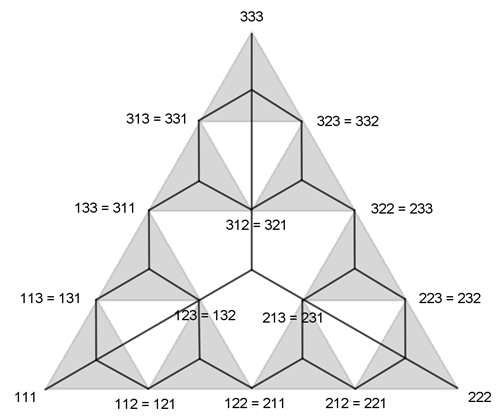
Das Dreieck (Initiator) als
Ausgangsfigur wird in vier kongruente
Geometrische Überlegungen Fläche des so entstandenen Dreiecks nach dem n-ten Schritt: An =
Das Sierpinski-Dreieck ist die Menge der Punkte der Ebene, die übrigbleiben, wenn man das Verfahren unendlich oft wiederholt. Für
n
→ ∞ gilt:
An → 0 Randlänge der Dreiecke nach dem n-ten Schritt: l n =
Für
n
→ ∞ gilt:
ln → ∞ , d.h. die
Randlänge des Sierpinski-Dreiecks geht gegen unendlich.
Dimension D eines Fraktals Bei selbstähnlichen Strukturen gilt folgende Definition für die Dimension D: D =
Strecke: D =
Quadrat: D =
Sierpinski-Dreieck:
D =
Das Chaos-Spiel (Michael F. Barnsley) Man nehme ein Blatt Papier und einen Bleistift und markiere z.B. die Ecken eines gleichseitigen Dreiecks als Punkte 1, 2 und 3 (Bezugspunkte). Dann benötigt man einen Würfel, mit dem die Zahlen 1, 2 und 3 mit gleicher Wahrscheinlichkeit gewürfelt werden können (z B. 1 oder 6 entspricht 1, 2 oder 5 entspricht 2, 3 oder 4 entspricht 3). Man beginne das Spiel mit einem beliebigen Punkt auf dem Blatt, der markiert wird (Spielpunkt). Nun wird gewürfelt. Wenn z.B. die Zahl 2 erscheint, setzt man einen Punkt genau in die Mitte zwischen Spielpunkt und Bezugspunkt 2. Mit diesem neuen Punkt als Spielpunkt wiederholt man Würfeln und Punkte setzen. Es entsteht eine Reihe von zufallsbedingt erzeugten Punkten.
Nach etwa 500 Spielpunkten
wird ein Muster sichtbar und nach etwa 10000 Punkten (s. nebenstehendes
Bild) wird bereits deutlich die Struktur des Sierpinski-Dreiecks sichtbar.
Je größer die
Anzahl der Schritte beim Chaos-Spiel ist, um so mehr nähern sich die
Spielpunkte dem Sierpinski-Dreieck (Attraktor).
Die Menge aller σ
= s1s2s3...
mit si ϵ {1, 2, 3}, i ϵ {1, 2, 3, …} bilden den sog.
Adressenraum.
Die Adressen werden folgendermaßen gebildet: L(links) = 1, R(rechts) = 2,
T(top) = 3
Zwei verschiedene Elemente des
Adressenraums können jedoch demselben Punkt im Sierpinski-Dreieck angehören.
Damit kann dem Sierpinski-Dreieck umkehrbar eindeutig ein aus Zahlen
bestehender Adressenraum zugeordnet werden.
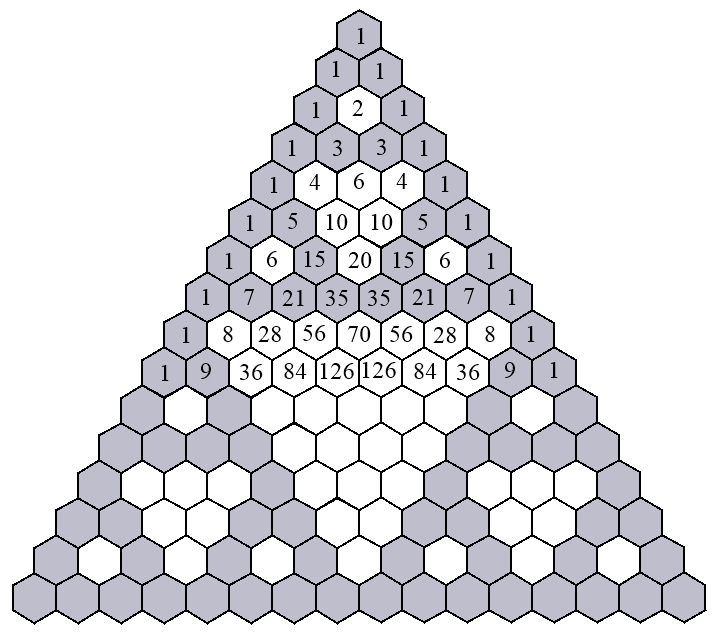
Das Pascalsche
Dreieck und das Sierpinski-Dreieck
Werden im Pascalschen Dreieck
mit 16 Zeilen die ungeraden Zahlen durch dunkle Sechsecke und
die geraden Zahlen durch helle Sechsecke dargestellt, ergibt sich eine Ähnlichkeit
zum Sierpinski-Dreieck.
Pascalsches Dreieck mit 64 Zeilen,
Bodenmosaik in der Kirche S. Maria in Trastevere in Rom
Sierpinskidreieck als Weihnachtsbaum
Zurück Zurück zur Startseite |



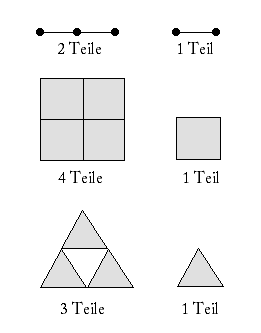 Beispiele:
Beispiele: