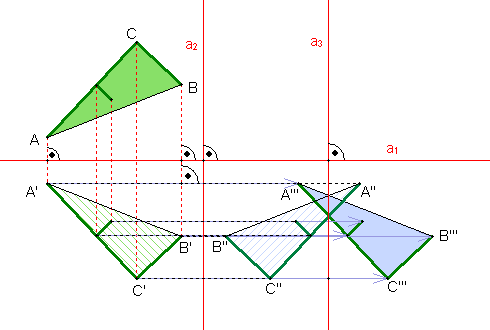
Achsenspiegelungen
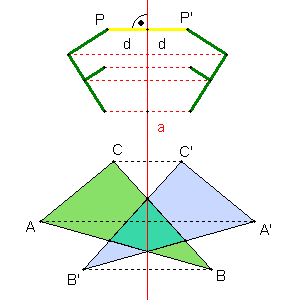
Definition Bildet man jeden Punkt P einer Figur auf einen Bildpunkt P’ ab, der bezüglich einer Achse a symmetrisch zu P liegt, so heißt diese Abbildung Achsenspiegelung.
Eigenschaften der Achsenspiegelung 1) Die Verbindungsstrecke Punkt Bildpunkt wird von der Achse halbiert und steht darauf senkrecht. 2) Geraden werden auf Geraden, Kreise auf Kreise mit gleichem Radius abgebildet. 3) Strecken werden auf gleich lange Strecken und Winkel werden auf gleich große Winkel abgebildet. 4) Die Achsenspiegelung kehrt den Umlaufsinn um. Mehrfachspiegelungen
a)
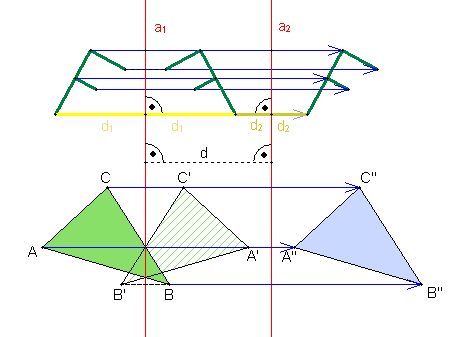
Die Verschiebung (Translation) Verschiebt man jeden Punkt einer Figur gleich weit in dieselbe Richtung, so entsteht eine Bildfigur. Diese Abbildung heißt Verschiebung (Translation).
Eigenschaft der Verschiebung Eine Zweifachspiegelung an parallelen Achsen mit dem Abstand d ist gleichwertig mit einer Verschiebung um 2d senkrecht zu den Achsen. b)
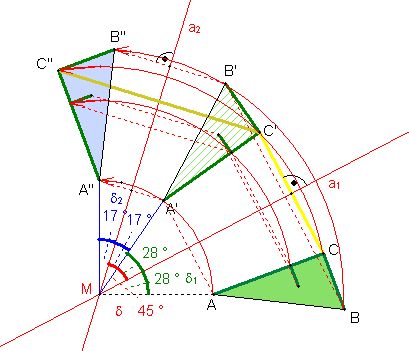
Die Drehung (Rotation)
Bewegt man jeden Punkt P einer
Figur auf einem Kreis um den festen Punkt M mit dem Radius MP um den Drehwinkel
j, so entsteht eine Bildfigur. Diese Abbildung heißt
Drehung (Rotation) um den
Drehpunkt M.
Eigenschaft der Drehung Eine Zweifachspiegelung an Achsen, die sich im Schnittpunkt M unter dem Winkel d schneiden, ist gleichwertig mit einer Drehung um M mit dem Drehwinkel j = 2d .
c)
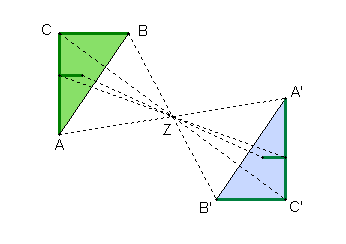
Die Punktspiegelung
Eine Drehung um den Drehpunkt Z
mit dem Drehwinkel 180° ist eine Punktspiegelung.
Eigenschaft der Punktspiegelung Punkt und Spiegelpunkt einer Punktspiegelung bestimmen eine Strecke, die vom Zentrum Z halbiert wird.
d)
Die Gleitspiegelung Eine Gleitspiegelung ist eine Hintereinanderausführung von Achsenspiegelung und Verschiebung parallel zur Achse oder umgekehrt.
Eigenschaft der Gleitspiegelung Eine Gleitspiegelung lässt sich durch eine Dreifachspiegelung an zwei parallelen Achsen und einer dazu senkrechten Achse erzeugen. |