|
Regelmäßige Vielecke (Polygone, n-Ecke)
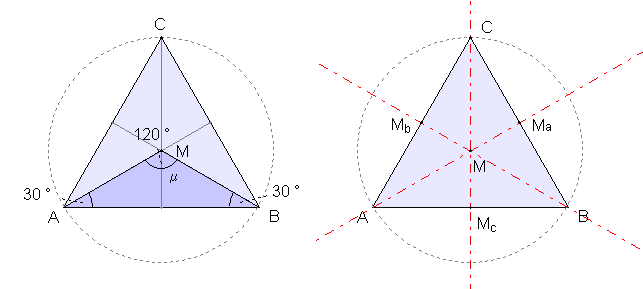
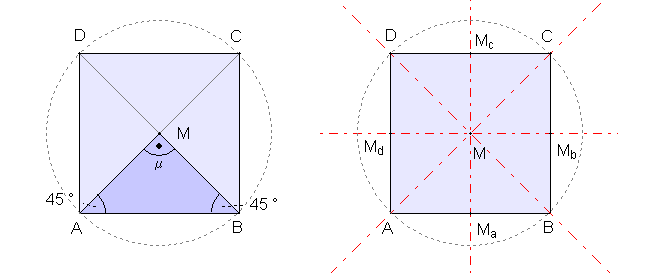
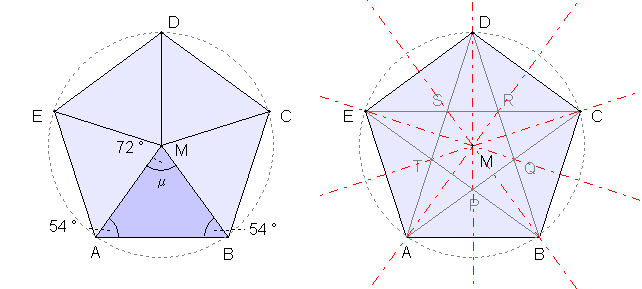
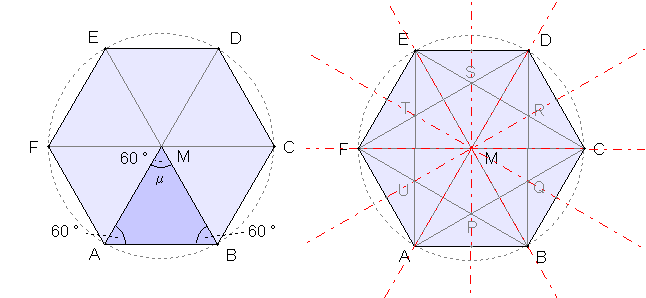
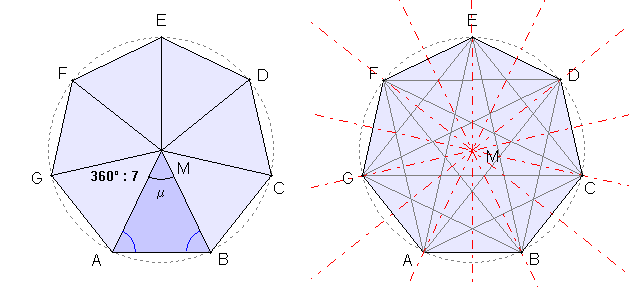
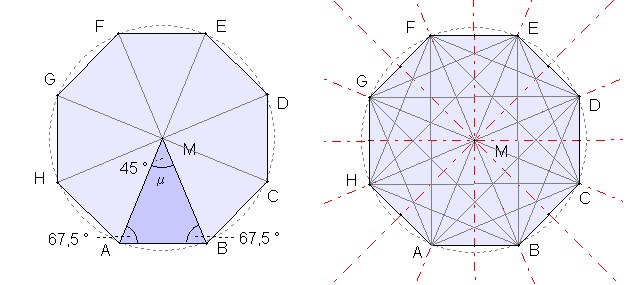
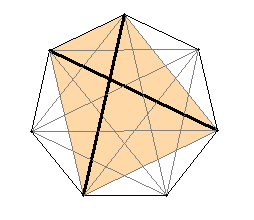
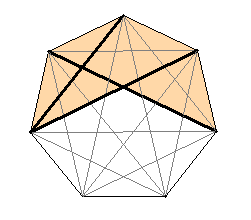
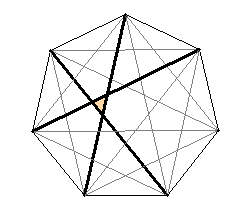
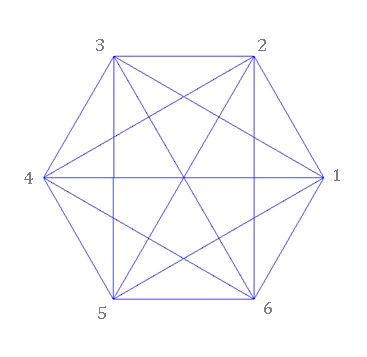
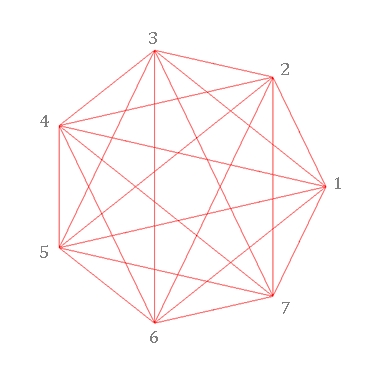
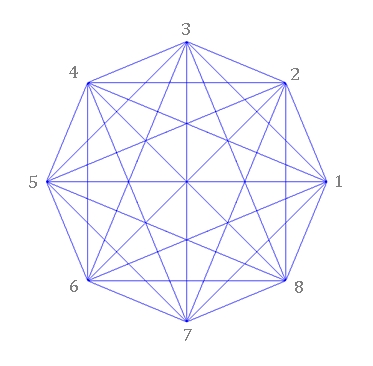
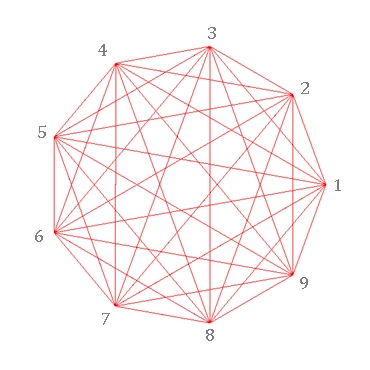
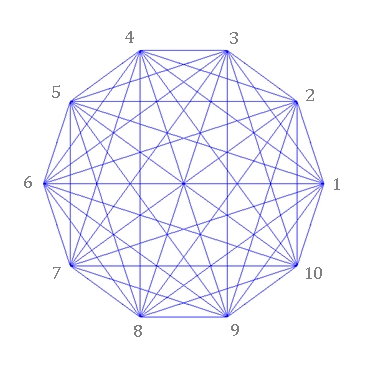
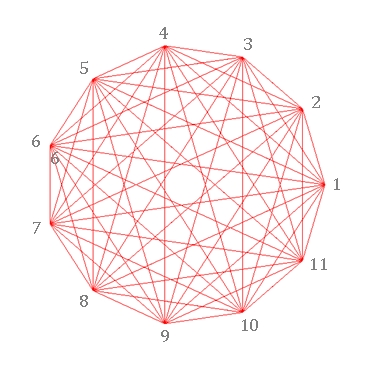
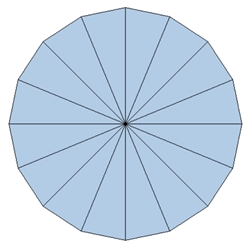
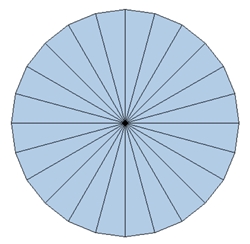
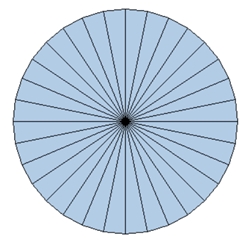
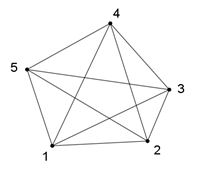
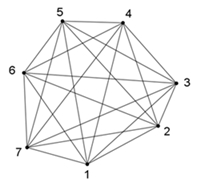
Regelmäßige n-Ecke von n = 3 bis
8: Links mit Bestimmungsdreieck, rechts mit Diagonalen und Symmetrieachsen
Eigenschaften eines regelmäßigen
n-Ecks:
Spezielle Eigenschaften von regelmäßigen n-Ecken:
n = 6: k1 = 3; k2 = 1 n = 8: k1 = 21; k2 = 12
Es
gilt:
Erklärung zur 2. Spalte in der Tabelle: Mit Abzählen und geschickter Summation: Vom 1. Eckpunkt gehen n-1, vom 2. Eckpunkt n-2 Verbindungslinien und vom letzten Eckpunkt 1 Verbindungslinie aus. Eine geschickte Summierung aller Verbindungslinien (1. + letzter, 2. + vorletzter usw.) liefert [(n-1)+1] + [(n-2)+2] + ..., das sind (n-1)/2 Summanden n.
Mit
Kombinatorik: Da
jeweils 2 von n Punkten verbunden werden, gibt es
Erklärung zur 4. Spalte in der Tabelle:
Falls
es keine Mehrfachschnittpunkte der Diagonalen gibt liefern jeweils die
Verbindungsstrecken von vier verschiedenen Punkten des n-Ecks einen
Diagonalschnittpunkt. Nach den Regeln der Kombinatorik gibt es dann insgesamt
Erklärungen zur 6. Spalte in der Tabelle:
1. Fall:
Ein Dreieck entsteht im n-Eck durch die
Verbindungsstrecken dreier verschiedener Eckpunkte. Es gibt dafür
2. Fall: Durch die
Verbindungsstrecken von vier verschiedenen Eckpunkten gibt es weitere
3. Fall:
Durch die
Verbindungsstrecken von fünf verschiedenen Eckpunkten gibt es weitere
4. Fall: Schließlich erhält man durch die
Verbindungsstrecken von sechs verschiedenen Eckpunkten noch
zusätzlich
Typischer Unterschied im Verlauf der Diagonalen bei einem geradzahligen und ungeradzahligen regelmäßigen n-Eck:
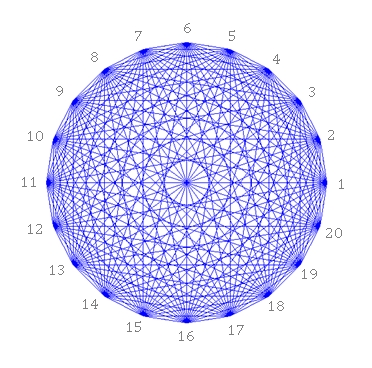
Ist die Eckenzahl gerade, so verlaufen die Diagonalen durch den Mittelpunkt.
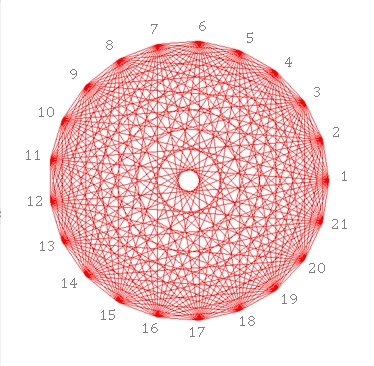
Bei ungerader Eckenzahl ist die Mitte leer und die Diagonalen bilden innen
ein verkleinertes n-Eck.
Konzentrische 16-Ecke und ein 8-Eck mit Diagonalen
Fensterrosetten in
Kathedralen
Reguläre Vielecke als Grundstruktur für
Fensterrosetten
in Kathedralen
12eck
16eck
24eck
32eck
Zugehörige Fensterrosetten
Notre-Dame Chartre
Notre-Dame
Reims W-Rosette Notre-Dame Paris S-Rosette
Straßburger Münster
Quelle für die Fensterrosetten: Wikipedia
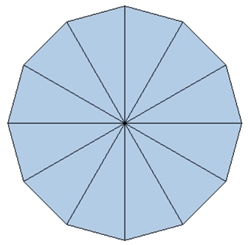
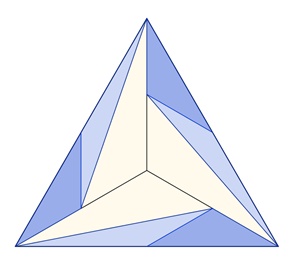
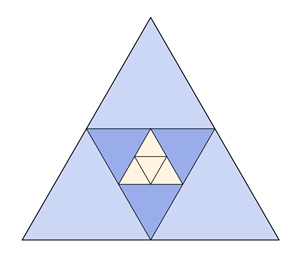
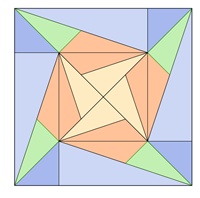
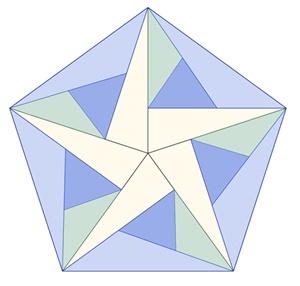
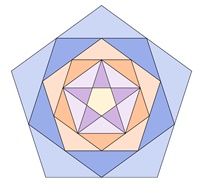
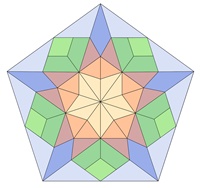
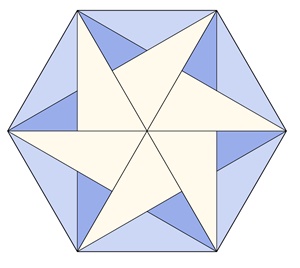
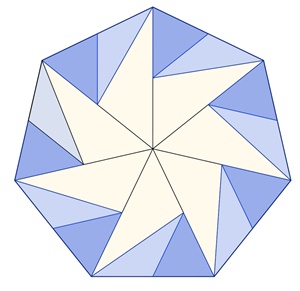
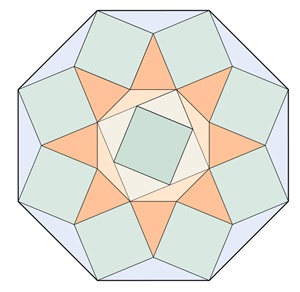
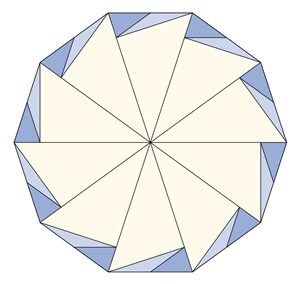
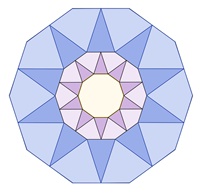
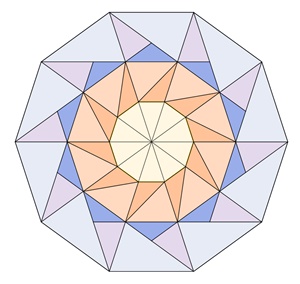
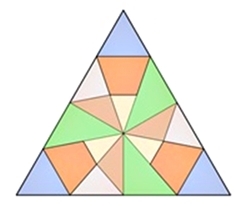
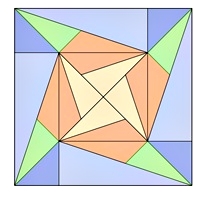
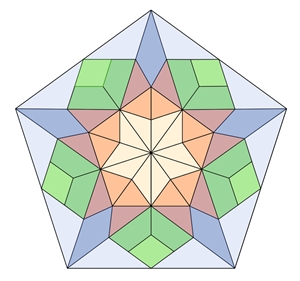
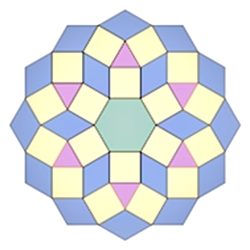
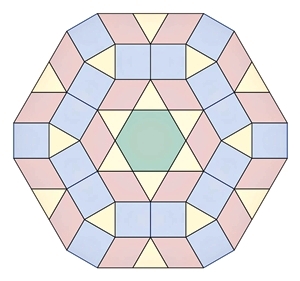
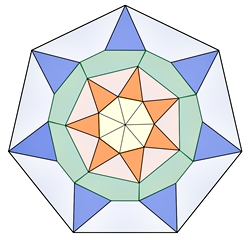
Bilder einer Unterteilung regulärer Vielecke
Gleichseitiges Dreieck:
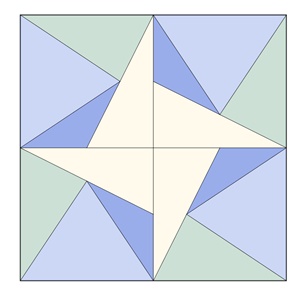
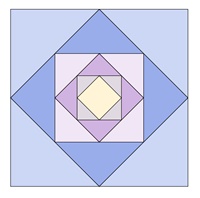
Quadrat:
Reguläres Fünfeck:
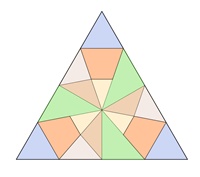
Reguläres Sechseck:
Reguläres Siebeneck:
Reguläres Achteck:
Reguläres Zehneck:
Kongruente Teilflächen in den einzelnen
Vielecken sind mit gleicher Farbe dargestellt.
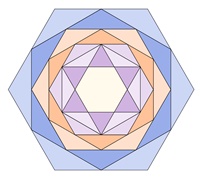
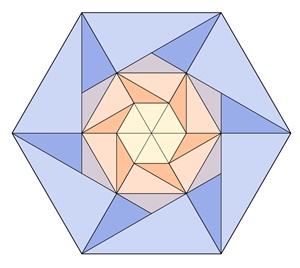
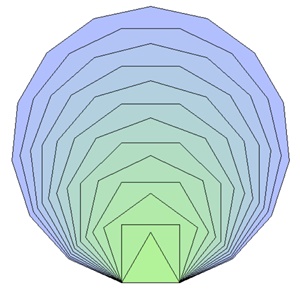
Vom gleichseitigen Dreieck zum regelmäßigen 15-Eck:
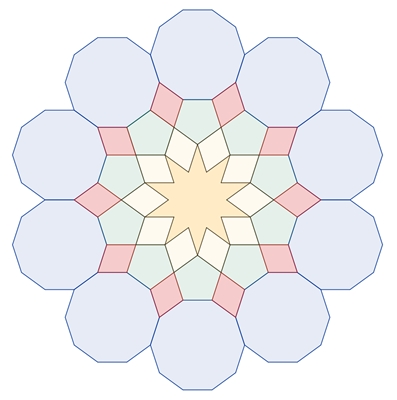
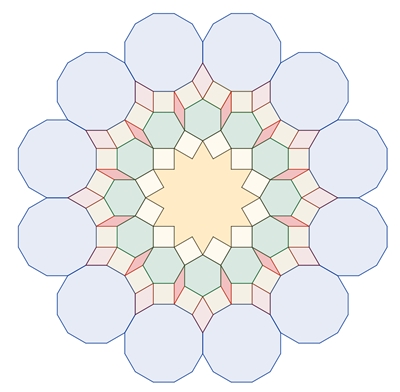
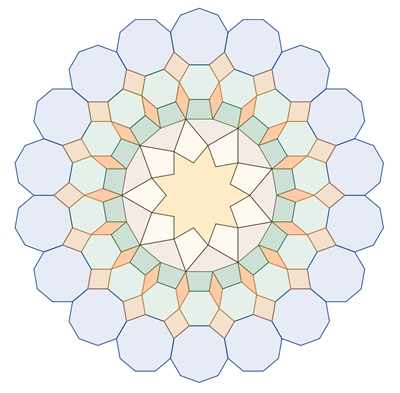
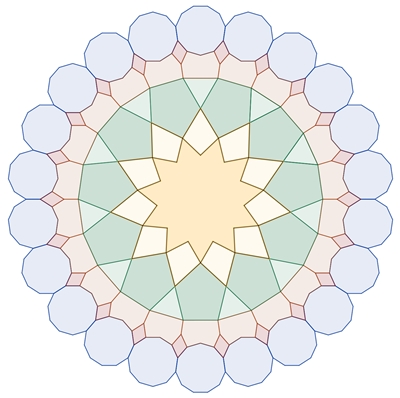
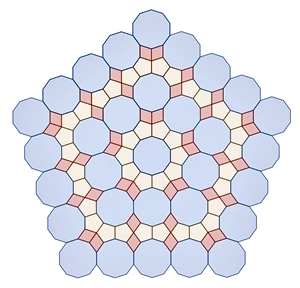
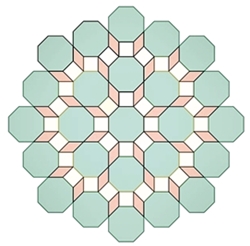
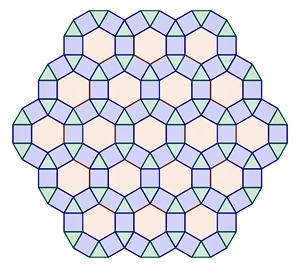
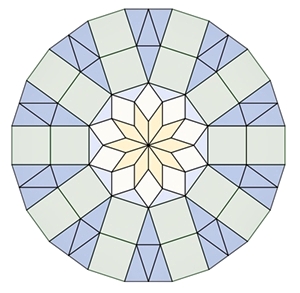
Kränze (ringförmige Anordnung)
von regulären Vielecken mit Sternen im Inneren
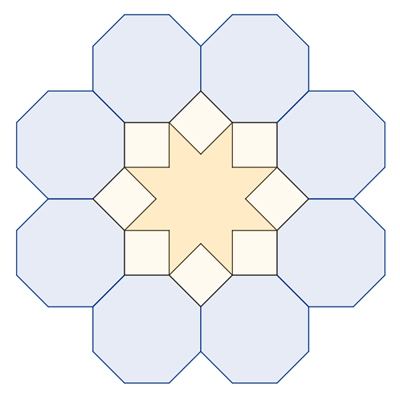
Reguläre Vielecke mit gerader
Eckenzahl 2n, n
∈ {3, 4, 5, 6, …}
Die Anzahl der regulären Vielecke,
die einen Kranz bilden entspricht der Eckenzahl.
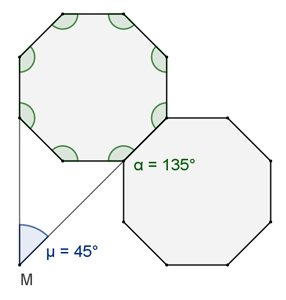
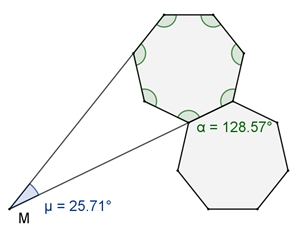
Begründung der Kranzbildung für n
= 8:
Innenwinkel
𝛼
des regulären Achtecks:
Drehwinkel
μ
= 360° – 2٠(180°
–
𝛼)
– (360° - 𝛼)
= 45°
8 ٠ 45° =
360°, d.h 8 angrenzende reguläre
Achtecke bilden einen Kranz
Allgemein gilt für das reguläre
2n-Eck: n
∈ {3, 4, 5, 6, …}
Innenwinkel
𝛼
des regulären 2n-Ecks:
Drehwinkel
μ
= (n – 2)٠
180° – 2٠(180°
–
𝛼)
– (2n – 6)/2٠(360°
– 𝛼)
2n 2n-Ecke bilden einen Kranz.
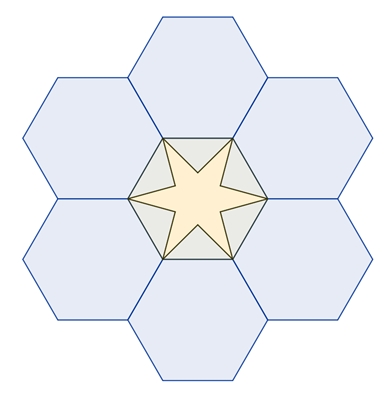
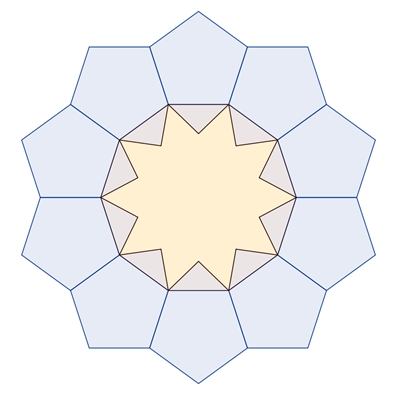
Reguläre Vielecke mit ungerader
Eckenzahl 2n-1, n
∈
{3, 4, 5, 6, …}
Die Anzahl der regulären
Vielecke, die einen Ring bilden entspricht der doppelten Eckenzahl.
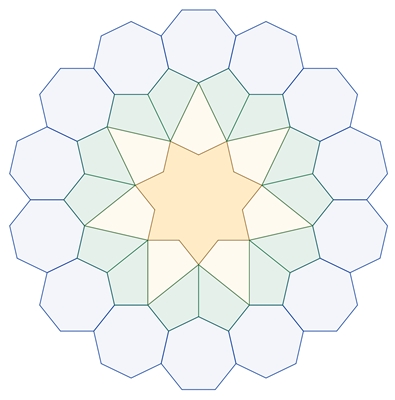
Begründung der Kranzbildung für n =
7:
Innenwinkel
𝛼
des regulären Sechsecks:
Drehwinkel
μ
= 360°– 2٠(180°–
𝛼)
– (360°– 𝛼)
≈ 25,71°
14 ٠ μ =
360°, d.h 10 angrenzende reguläre Siebenecke bilden einen Kranz.
Allgemein gilt für das reguläre
(2n–1)-Eck: n
∈ {3, 4, 5, 6, …}
Innenwinkel
𝛼
des regulären (2n–1)-Ecks:
Drehwinkel
μ
= (n – 2)٠
180° – 2٠(180°
–
𝛼)
– (2n – 6)/2٠(360°
– 𝛼)
2٠(2n–1)
(2n–1)-Ecke
bilden einen Kranz.
Regelmäßige n-Ecke – Berechnungen
Umkreisradius R:
sin(π/n)
= a/2 /R (Sinus im Dreieck A2N1M)
R = a / (2 sin(π/n))
Inkreisradius r:
cot(π/n)
= r
/ a/2 (Kotangens
im Dreieck A1N1M)
r = a/2 cot(π/n)
Flächeninhalt A
= n mal Flächeninhalt im Dreieck A1A2M
A = n٠a٠r/2
= n a2/4٠cot(π/n)
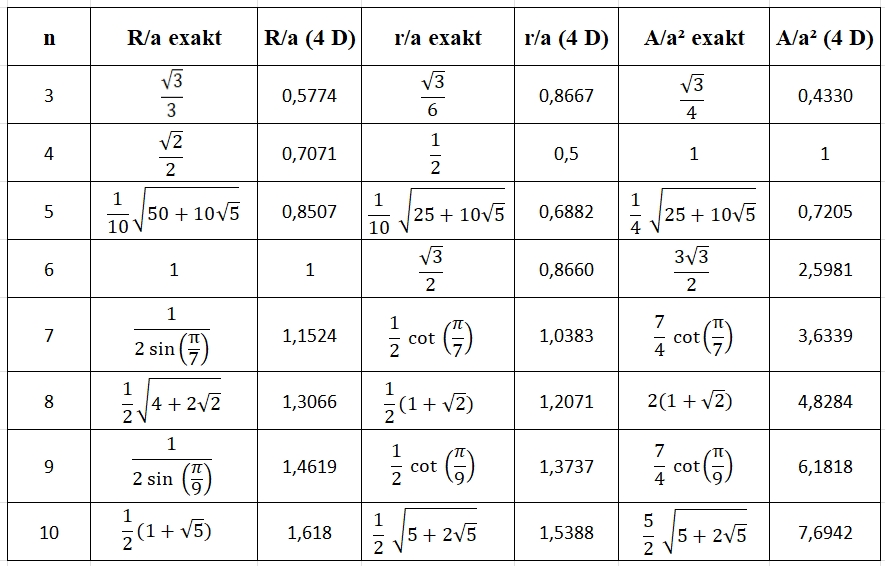
Tabelle für n-Ecke von n=3 bis
n=10
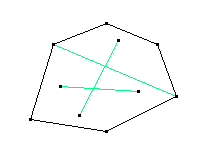
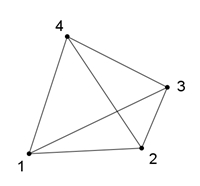
Unregelmäßige konvexe Vielecke Definition eines unregelmäßigen konvexen n-Ecks: Ein n-Eck heißt unregelmäßig konvex, wenn nicht alle Seiten gleich lang sind und die Verbindungsstrecken beliebiger Punkte des n-Ecks im n-Eck enthalten sind.
Allgemein gilt: Die Winkelsumme im n-Eck beträgt 180°٠(n – 2).
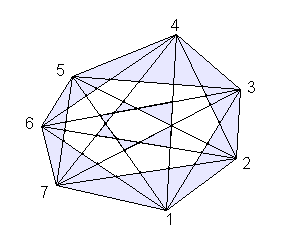
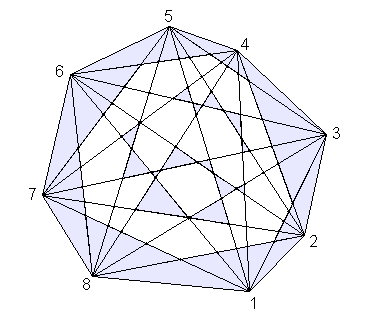
Unregelmäßige konvexe
Sieben- und Achtecke ohne Mehrfachschnittpunkte der Diagonalen, die sich nicht überdeckenden
Dreiecke sind farbig dargestellt: Spezielle Eigenschaften von unregelmäßigen
konvexen n-Ecken ohne Mehrfachschnittpunkte der Diagonalen:
Erklärungen zur letzten Zeile siehe regelmäßige Vielecke!
Anzahl der maximalen
Schnittflächen (Teilpolygone) in einem n-Eck
Das Viereck hat 4, das Fünfeck hat 11, das
Sechseck
hat maximal 25, das Siebeneck hat maximal 50 Schnittflächen
Die maximale Anzahl von Schnittflächen
(Teilpolygonen) entsteht, wenn sich nur zwei Diagonalen in einem Punkt
schneiden.
Formel für die maximale Anzahl Amax
der Schnittflächen eines unregelmäßigen konvexen n-Ecks:
Tabelle
für die maximale Anzahl Amax
der Schnittflächen in Abhängigkeit von n:
Für regelmäßige n-Ecke mit ungerader Eckenzahl gelten die
Tabellenwerte ebenfalls, da sich dann nur zwei Diagonalen in einem Punkt
schneiden.
Muster mit Vielecken
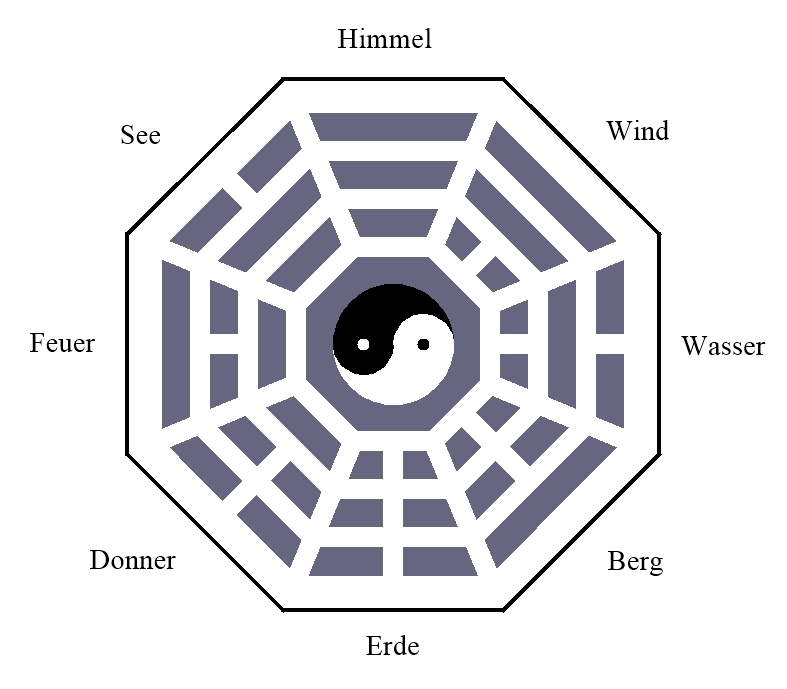
Acht Trigramme (Chinesische Symbole, hier
mit Zuordnung zur Natur)
Parkette mit regelmäßigen
Vielecken Zurück Zurück zur Startseite |