Wachstumsmodelle

Lineares Wachstum

Positives Wachstum bedeutet Zunahme, negatives Wachstum Abnahme.

Die lineare Funktion mit der Gleichung  f(t) = m٠t + c  
stellt für m > 0  positives Wachstum und für m < 0  negatives Wachstum dar, wobei gilt:  f(0) = c  und  t ≥ 0 (t für Zeit).

Beispiel: 

Funktionsgraphen für c = 3, m = 0,5 (grün) und m = - 0,6 (blau)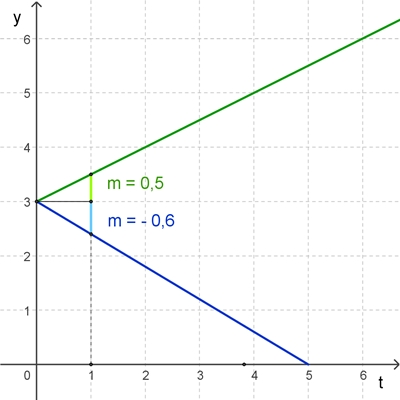

Exponentielles Wachstum und exponentieller Zerfall

Die Exponentialfunktion mit der Gleichung

f(t) = b٠a^t
stellt mit der Basis a > 1 Wachstum und  0 < a < 1 Zerfall dar, wobei gilt:
f(0) = b٠a⁰ = b  und Exponent Zeit t ≥ 0.

Beispiel: 

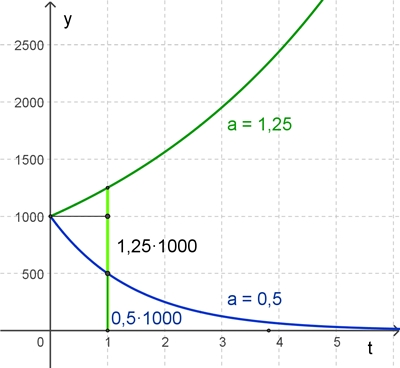
Graphen der Funktionen für b = 1000 und

a = 1,25 für Wachstum (grün) und a = 0,5 für Zerfall (blau)

Eigenschaften des exponentiellen Wachstums:

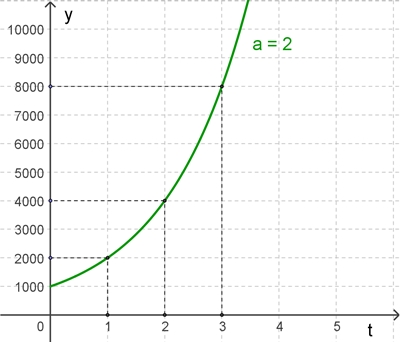
Beispiel:    f(t)  =  1000٠2^t, t ≥ 0

Graph der Funktion (grün)

 
Für  t = 0, 1, 2, 3, … gilt  y = 1000, 2000, 4000, 8000, …

Das bedeutet, dass bei gleichem zeitlichen Abstandwert 1 der Wert von y sich verdoppelt, vervierfacht, verachtfacht, usw., d.h. der Wert von y nimmt um den Faktor 2¹, 2², 2³ . . . exponentiell zu.

Bei zunehmend gleichem Abstandswert Δt verdoppelt sich jeweils der Wert von y.

Eigenschaften des exponentiellen Zerfalls:

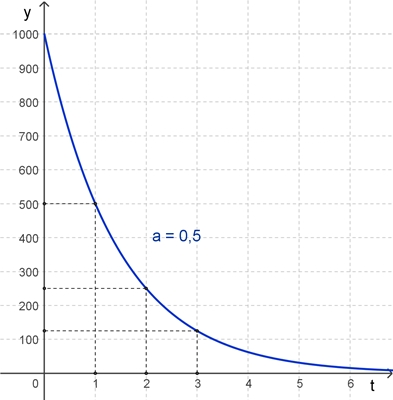
Beispiel:    f(t)  =  1000٠0,5^t, t ≥ 0

Graph der Funktion (blau)

Für  t = 0, 1, 2, 3, … gilt  y = 1000, 500, 250, 125, …

Das bedeutet, dass bei gleichem zeitlichen Abstand 1 der Wert von y um den Faktor 1/2, 1/2² =1/4, 1/2³ =1/8. . . exponentiell abnimmt.

Bei zunehmend gleichem Abstandswert Δt halbiert sich jeweils der Wert von y.

Begrenzter Zerfall

Die Funktion mit der Gleichung

f(t) = g + (f(0) - g)٠a^t

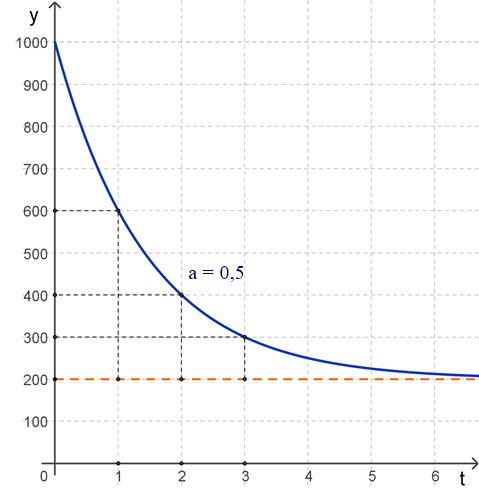
stellt mit 0 < a < 1 und  t ≥ 0 begrenzten Zerfall dar.

Beispiel:  g = 200, f(0) = 1000, a = 0,5

f(t)  =  200 + (1000 - 200)٠0,5^t,  t ≥ 0

Graph der Funktion (blau)

Begrenztes Wachstum

Die Funktion mit der Gleichung

f(t) = g - (g - f(0))٠a^t

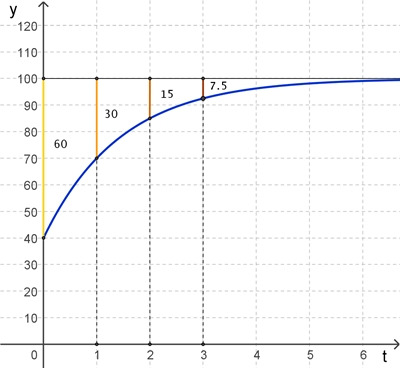
stellt mit 0 < a < 1 und  t ≥ 0 begrenztes Wachstum dar.

Beispiel:   g = 100, f(0) = 40, a = 0,5

f(t)  =  100 - (100 - 40)٠0,5^t,  t ≥ 0

Graph der Funktion (blau)

Logistisches Wachstum

Die Funktion mit der Gleichung

mit 0 < a < 1 und  t ≥ 0 heißt logistische Funktion, g = logistische Schranke, c = f(0)  

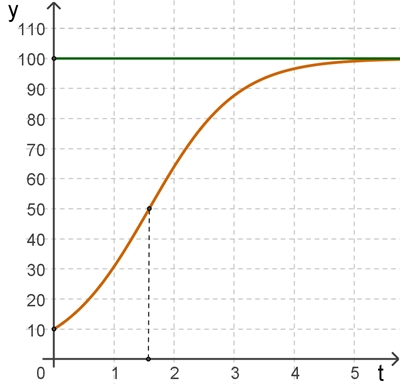
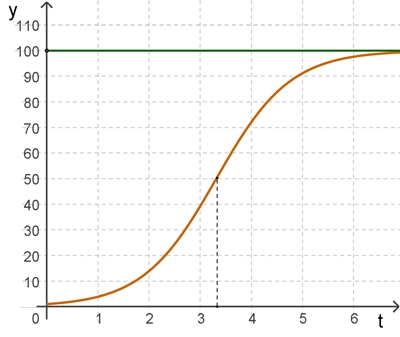
Beispiele:   g = 100, c = 10, b = 2, a = 0,5,            g = 100, c = 1, b = 2, a = 0,5,

Funktionsgraphen G_f

Bei  t ≈ 1,6  bzw. t ≈ 3,3 liegt jeweils der Wendepunkt zwischen zunehmender und abnehmender Wachstumsgeschwindigkeit.

Bemerkungen:

Die Exponentialfunktion wird oft aus mathematischen Gründen mit der Basis e ≈ 2,71828 (Eulersche Zahl) dargestellt:

 f(t) = b٠e ^k٠t  an Stelle von  f(t) = b٠a^t, wobei gilt:

e ^kt = a ^t   ⇔  ln e ^k٠t = ln a ^t   ⇔   k٠t = t٠ln a  ⇔  k = ln a

Es gibt weitere Funktionen, die in Teilen Wachstumsprozesse angenähert darstellen können, z.B. Polynomfunktionen, trigonometrische Funktionen, Räuber-Beute-Gleichungen.

Natürliches Wachstum wird von vielen Randbedingungen beeinflusst.

Mathematische Modelle können den tatsächlichen Verlauf des Wachstums nur annähern.

Da Ressourcen begrenzt und endlich sind, wird jedes Wachstum an eine Grenze gelangen. Exponentielles Wachstum kann es nur in einer Anfangsphase geben.

Begrenztes Wachstum kann mit Hilfe einer variierten Exponentialfunktion oder durch die logistische Funktion angenähert werden.