|
Al Chwarizmi (ca. 783 – 850) Al Chwarizmi wurde im Gebiet von Chiwa, heute
Usbekistan, geboren, das ihm ein würdiges Denkmal gestiftet hat (s. Foto).
Er hat jedoch den größten Teil seines Lebens in Bagdad,
der Hauptstadt der Abbasiden-Kalifen,
verbracht.
Denkmal von Al-Chwarizmi in Chiva / Usbekistan, Foto: M.
Holzapfel Al-Chwarizmi hat sich mit elementarer
Algebra beschäftigte. Auch leistete er
bedeutende Beiträge als Geograph und Kartograph.
In seinem Buch über die Indische
Zahlschrift (um 825)
stellte al-Chwarizmi die Arbeit mit Dezimalzahlen vor
und führte die Ziffer Null aus
dem indischen in das arabische Zahlensystem und damit in alle modernen
Zahlensysteme ein. Aus dem Titel eines seiner Werke
al-ǧabr wurde der Begriff
Algebra abgeleitet. Ein weiteres Hauptwerk al-Chwarizmis (um 833) ist
das Buch über das Bild der Erde Kitāb
Ṣūrat al-arḍ. Es handelt sich um eine überarbeitete und erweiterte
Fassung der Geografie von Ptolemäus.
Fibonacci (um 1170 – 1240 Pisa) Leonardo da Pisa,
genannt Fibonacci („figlio
di Bonacci“, Sohn des Bonacci
aus Pisa), kam bereits mit ca. 20 Jahren mit der Mathematik in den
islamischen Ländern in Kontakt und studierte sie eifrig. Diese vorwiegend
arabischen Länder übernahmen das
indische Dezimalsystem und das
Buch die Elemente von
Euklid, deren Inhalte in Europa
im frühen Mittelalter fast vollständig verloren gingen. Die Elemente,
in denen der griechische Mathematiker Euklid um
300 v. Chr. die Geometrie seiner Zeit systematisch zusammengefasst hatte,
lagen im späten 8. Jahrhundert in arabischer Übersetzung vor und hatten
einen sehr großen Einfluss auf die islamischen Mathematiker. Die Elemente
des Euklid stellen auch heute noch die Grundlage der geometrischen
Ausbildung im Gymnasium und der weiteren Fortbildung dar. Das Hauptwerk von
Fibonacci ist das Liber
abbaci. Der Titel kann man mit „Buch der Rechenkunst“ übersetzen. Es ist
etwa 1202 entstanden, zweite Fassung ca. 1227. In ihm stellte Fibonacci das
Wissen zusammen, das er während seiner Aufenthalte in arabischen Länder
erworben hatte, und verband es mit eigenen Überlegungen und Ausarbeitungen.
Das Resultat ist ein Werk, das für lange Zeit die Geschichte der
abendländischen Mathematik bestimmen sollte.
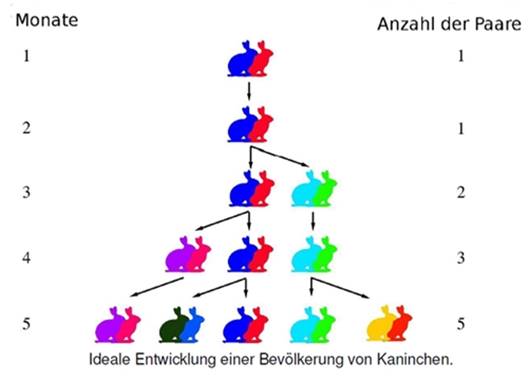
Etwa im Jahre 1202 interessierte sich Fibonacci für das
Wachstumsproblem einer Kaninchen-Population unter idealen
Umständen. Das Problem kann wie folgt formuliert werden:
• man fängt mit einem Paar junger Kaninchen an,
• ein einmonatiges Kaninchen ist fähig sich fortzupflanzen,
• ein Kaninchenpaar (im Fortpflanzungsalter) gebärt jeden Monat ein weiteres
Kaninchenpaar.
Fibonacci stellte sich folgende Frage: Wie viele Kaninchenpaare wird es nach
einem Jahr geben?
Quelle:
https://www.srf.ch/sendungen/einstein/big-data-das-grosse-vermessen/die-mathematik-der-pflanzen Fibonacci weist bei seiner Zahlenfolge darauf hin,
dass sich jedes Glied der Reihe durch Summierung der beiden vorhergehenden
Reihenglieder errechnen lässt. Eine weitere Beschäftigung mit dieser Folge
findet sich bei ihm nicht, d. h., der Zusammenhang zum Goldenen Schnitt wird
von ihm nicht dargestellt. Fibonacci-Folge:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, . . . Fibonacci-Folge im Museum Brandhorst, München
Foto: M. Holzapfel
Adam Ries(e) (ca. 1492 – 1559) Adam Ries(e)
verbreitete das Rechnen mit
Stellenwertsystem und arabischen Ziffern in Erfurt und Annaberg in seiner
Rechenschule und gab das Lehrbuch
Rechnung auff der Linihen und
Federn (126 Seiten gedruckt) in deutscher Sprache heraus. Dadurch lernte
eine breitere Bevölkerungsschicht das Rechnen mit arabischen Ziffern kennen. Sein Name ist aus der Redewendung „Das
macht nach Adam Riese …“ allgemein
bekannt. Auszug aus seinem Lehrbuch von Seite 12 (Auflage von
1533):
|