Mathematikgeschichte der Neuzeit im Überblick

Als Mathematiker tat sich Kepler noch durch seine Behandlung der allgemeinen Theorie der Vielecke und Vielflächner hervor. Mehrere bis dahin unbekannte Raumgebilde entdeckte und konstruierte er völlig neu, unter anderem das regelmäßige Sternvierzigeck. In seinem 1596 veröffentlichten Buch Mysterium Cosmographicum (Das Weltgeheimnis) versuchte Kepler, die Bahnen der damals bekannten fünf Planeten Merkur, Venus, Mars, Jupiter und Saturn mit der Oberfläche der fünf platonischen Körper in Beziehung zu setzen. Die Umlaufbahn des Saturns stellte er sich dabei als Großkreis auf einer Kugel noch nicht als Ellipse vor, die einen Würfel (Hexaeder) umschließt. Der Würfel umschließt wiederum eine Kugel, welche die Jupiterbahn beschreiben soll (siehe Abbildung). Diese Kugel wiederum schließt ein Tetraeder ein, das die Marskugel umhüllt. Dieses schöne mathematische Konzept war nach Keplers Entdeckung des ersten nach ihm benannten Gesetzes wieder als zu ungenau in Frage gestellt.

1609 veröffentlichte Kepler in dem Werk Astronomia nova (Neue Astronomie) seine beiden ersten Keplerschen Gesetze.

1619 verfasste er sein Hauptwerk Harmonices Mundi Libri V (5 Bücher zur Harmonie der Welt, mit Kapiteln zur Geometrie, Harmonielehre, Astronomie und Metaphysik), in dem er auch neben den ersten beiden das dritte Keplerschen Gesetze veröffentlichte.

Erstes Keplersches Gesetz

Die Planeten bewegen sich auf elliptischen Bahnen. In einem ihrer Brennpunkte steht die Sonne.

Zweites Keplersches Gesetz

Eine ungerade Primzahl p ist genau dann die Summe zweier Quadrate, wenn sie von der Form p = 4 n +1 ist:

Kleiner Fermatscher Satz:
Für jede Primzahl gilt:

Leibniz war ein vielseitig interessierter und gelehrter Mensch. Er war Mathematiker, Philosoph, Jurist, Historiker, politischer Berater und Vordenker der Aufklärung.

Newton war Mathematiker, Physiker und Philosoph. Er legt den Grundstein für die klassische Mechanik in seinem Werk Philosophiae Naturalis Principia Mathematica  über Gravitation und Bewegungsgesetze.

Etwa zeitgleich und unabhängig zu Leibniz entwickelte er die Infinitesimalrechnung und lieferte wichtige Beiträge zur Algebra und zur ebenen algebraischen Geometrie. In der numerischen Mathematik ist das Newton-Verfahren ein Approximationsalgorithmus zur numerischen Lösung von nichtlinearen Gleichungen und Gleichungssystemen.

Jakob Bernoulli (Basel 1655 – 1705 Basel)

Er war schweizer Mathematiker und Physiker.

In der Mathematik begründete er 1685 die Methode der vollständigen Induktion. 1689 veröffentlichte er eine Abhandlung über unendliche Reihen, und stellte kurz darauf erste Arbeiten zur Infinitesimalrechnung fertig, die auf das Werk von Leibniz aufbauen und  den neuen Begriff Integral verwenden.

In dem nach seinem Tod herausgegebenen Buch Ars conjectandi wurde Jakob Bernoulli ein wichtiger Wegbereiter der Wahrscheinlichkeitsrechnung, über die sich bereits Blaise Pascal und Pierre de Fermat im Jahr 1654 mit dem Teilungsproblem eines Glücksspiels Gedanken machten. In dem Buch von Bernoulli wird die Anwendung der Kombinatorik auf Glücks- und Würfelspiele beschrieben, und das (schwache) Gesetz der großen Zahlen formuliert.

Auf ihn gehen Begriffe wie Bernoulli-Experiment, Bernoulli-Kette zurück.

Ein Bernoulli-Experiment hat nur zwei Ergebnisse, Niete (0) oder Treffer (1), der mit einer Wahrscheinlichkeit p eintritt. Wiederholt man dieses Experiment, so bleibt die Trefferwahrscheinlichkeit immer gleich p.

Bei einer Bernoulli-Kette wird das Experiment n-mal wiederholt (Bernoulli-Kette der Länge n). Für X gleich Anzahl k der Treffer (1) gilt für die Wahrscheinlichkeit P:
                                        P(X = k) =  p^k (1 – p)^n-k

Mit der Variablen x an Stelle eines bestimmten k stellt es die Binomialverteilung dar.

Leonhard Euler (Basel 1707 – 1783 Sankt Petersburg)

Euler war Mathematiker, Physiker, Astronom, Geograph, Logiker und Ingenieur. Er gilt als Begründer der Analysismit dem Begriff der mathematischen Funktion. Er trug zur Weiterentwicklung vieler Zweige der Mathematik bei, wie z.B. Geometrie, Zahlentheorie, Infinitesimalrechnung, Graphentheorie und Topologie.

Sein gesamtes mathematisches Werk umfasst 74 Bände – ein bisher unerreichter Umfang. Er gilt als einer der bedeutendsten Mathematiker.

Die Basis des natürlichen Logarithmus  e ≈ 2,71828 wurde nach ihm benannt als Eulersche Zahl.

Die Formel, die eine Verbindung zwischen trigonometrischen Funktionen und komplexer Exponentialfunktion mittels komplexer Zahlen darstellt, heißt Eulerformel mit der imaginären Einheit i und φ ϵ ℝ:  e^iφ = cos(φ) + i٠sin(φ)

Eulersche Identität:    e^iπ = – 1

Euler entdeckte die Formel   E – K + F = 2  bezüglich Anzahl der Ecken (E), Kanten (K) und Flächen (F) eines konvexen Polyeders.

Die Lösung von Euler zum Königsberger Brückenproblem gilt als Beginn der Graphentheorie.

Pierre-Simon Laplace (Normandie 1749 – 1827 Paris)

Laplace war ein französischer Mathematiker, Physiker und Astronom. Er war mehr Physiker als Mathematiker. Für ihn war Mathematik nur eine Hilfswissenschaft für die Physik und Astronomie.

In der Mathematik gebührt ihm ein wesentlicher Anteil zur Entwicklung der Wahrscheinlichkeitsrechnung. In seinem zweibändigen Werk Théorie Analytique des Probabilités (1812) formulierte Laplace die Definition der Wahrscheinlichkeit, abhängiger und unabhängiger Ereignisse, des Erwartungswerts und des Laplace-Experiments (Zufallsversuch, bei dem die Wahrscheinlichkeiten aller möglichen Ergebnisse gleich sind) mit der Laplace-Formel für Wahrscheinlichkeit P(A) eines Ereignisses A:

P(A) =

Er verfasste auch Abhandlungen zu Extremwertproblemen und Differentialgleichungen.

 

Carl Friedrich Gauß (Braunschweig 1777 – 1855 Göttingen)

Gauß war Mathematiker, Physiker, Astronom, Statistiker und Landvermesser. Er galt  bereits zu seinen Lebzeiten als herausragender Mathematiker.

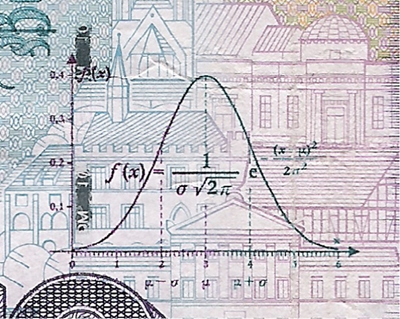
Gauß legte die Grundlagen von Statistik, Ausgleichsrechnung, nichteuklidischer Geometrie und Differentialgeometrie. Auf ihn gehen viele mathematische Funktionen, Integralsätze, die Normalverteilung (Gaußsche Glockenkurve) und erste Lösungen für elliptische Integrale zurück.

Vergrößerter Ausschnitt aus dem alten 10 DM Schein mit der Gaußschen Glockenkurve

Pafnuti Lwowitsch Tschebyschow (Okatowo 1821 – 1894 Sankt Petersburg)

Tschebyschow arbeitete auf den Gebieten Interpolation, Approximation, Funktionentheorie, Funktionentheorie, Zahlentheorie(Primzahltheorie) und Mechanik. Nach ihm sind viele Begriffe in der Wahrscheinlichkeitstheorie benannt, wie z.B. die Ungleichung von Bienaymé-Tschebyschow für die Abschätzung der Wahrscheinlichkeit P.
Besitzt eine Zufallsgröße X einen endlichen Erwartungswert μ und einen endlichen Varianzwert, dann gilt für jedes reelle c > 0 und die Wahrscheinlichkeit P:   
                                                  P(|X – μ| ≥ c)  ≤ 
Von ihm stammen auch die Tschebyschow-Polynome, die Tschebyschow-Distanz, der Tschebyschow-Filter, der Satz von Tschebyschow, Tschebyschows schwaches Gesetz der großen Zahlen, der Satz von Bertrand-Tschebyschow, die Tschebyschow-Summenungleichung, die Tschebyschow-Iteration und die Tschebyschow-Funktion.
 

David Hilbert (Königsberg 1862 – 1943 Göttingen)

Hilbert war bestrebt die mathematischen Teilgebiete axiomatisch zu begründen. In seinem Werk Grundlagen der Geometrie entwarf er für die euklidische Geometrie ein vollständiges Axiomensystem und entwickelte darauf aufbauend eine streng axiomatische und widerspruchsfrei begründete Geometrie.

Er verfasste auch wichtige Beiträge zur Variationsrechnung, Funktionalanalysis, Funktionenräumen (Hilbert-Raum) und partiellen Differentialgleichungen. Nach ihm wurden einige Mathematische Begriffe benannt.

Berühmt ist Hilberts Rede auf dem internationalen Mathematikerkongress in Paris im Jahre 1900, in der er eine Liste von 23 mathematischen Problemen vorstellte, die die mathematische Forschung des 20. Jahrhunderts nachhaltig beeinflusste.

 

Amalie Emmy Noether (Erlangen 1882 – 1935 Pensylvania)

Von ihr stammen grundlegende Beiträge zur modernen Algebra und zur theoretischen Physik. Sie war die zweite Deutsche, die an einer deutschen Universität in Erlangen in Mathematik promoviert wurde.

1920 begann Emmy Noether ihre Arbeiten in Abstrakter Algebra und
hat die Theorie der Ringe, Ideale und Körper entscheidend weiterentwickelt.

Ihr Schüler Bartel L. van der Waerden verfasste die zwei Bände Moderne Algebra, die auf den Vorlesungen von Emmy Noether aufbauten.

Bereits 1918 entwickelte Noether das sog. Noether-Theorem, das zu einer wichtigen Grundlage der theoretischen Physik wurde. Zu jeder Symmetrie eines physikalischen Systems gehört eine Erhaltungsgröße.

 

John von Neumann (Budapest 1903 – 1957 Washington)

Er lieferte wichtige Beiträge zur mathematischen Logik, Funktionalanalysis, Spieltheorie, Informatik und Quantenmechanik. Neumann gilt als einer der Begründer der Informatik. Nach ihm wurde 1945 die Von-Neumann-Architektur benannt, das ist ein Computer, in dem Daten und Programm im selben Speicher liegen. Dadurch waren Änderungen an Programmen schnell möglich ohne Änderungen an der Hardware durchzuführen.
Allerdings hatte Konrad Zuse schon 1936 einige Ideen der Von-Neumann-Architektur ausgearbeitet und bereits 1938 in der Z1-Maschine mechanisch realisiert.

Von Neumann arbeitete ab 1943 am Manhattan-Projekt in Los Alamos mit und war auch an der Entwicklung der Wasserstoffbombe beteiligt.

 

Andrei N. Kolmogorow (Tambow 1903 – 1987 Moskau)

Kolmogorow leistete wesentliche Beiträge auf dem Gebiet der Wahrscheinlichkeits-theorie und Topologie. Er gilt als Begründer der Algorithmischen Komplexitätstheorie. Seine bekannteste mathematische Leistung war die Axiomatisierung der Wahrscheinlichkeitstheorie.

Eine Funktion P: A → P(A), die jedem Ereignis A aus dem Ereignisraum (Menge aller Ereignisse) eine reelle Zahl P(A) zuordnet, heißt Wahrscheinlichkeitsverteilung, wenn sie folgende Bedingungen erfüllt:

Axiom I: P(A) ≥ 0
Axiom II: P(Ω) = 1
Axiom III: A B = Ø   ⇒   P(A ∪ B) = P(A) + P(B)

Kolmogorow veröffentlichte auch Beiträge zur Mengentheorie, Fourieranalysis und Integrationstheorie.

  

Kurt Friedrich Gödel (Brünn 1906 – 1978 Princeton)

Gödel war Mathematiker, Logiker und Philosoph.

Seine Arbeit mit dem Titel Über formal unentscheidbare Sätze stellte eine Grundlage der klassische Mathematik in Frage: Es gibt Aussagen, die weder bewiesen noch wiederlegt werden können.

Seinen Namen trägt der erste und zweite Gödelsche Unabhängigkeitssatz.

 
Quellenangabe:
Wikipedia
Bilder

---

Zurück zur Startseite