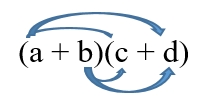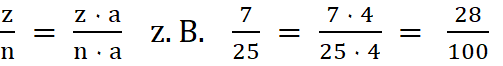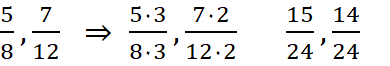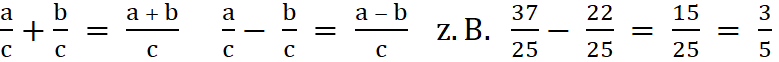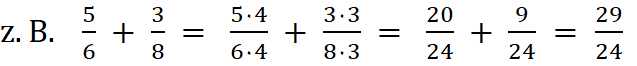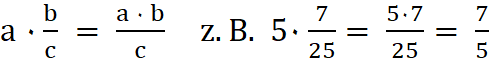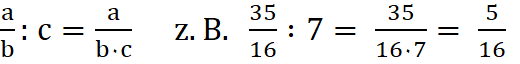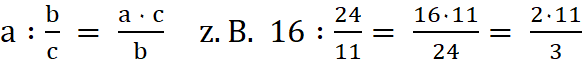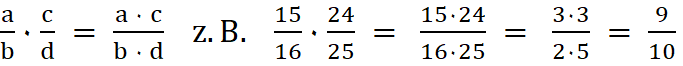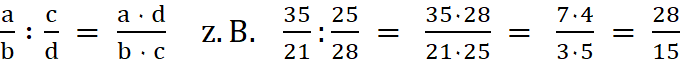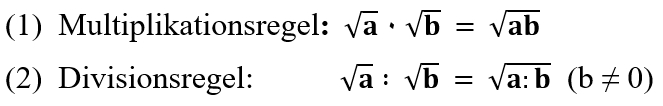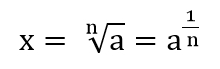Gesetze der elementaren Algebra

Von dem arabischen Gelehrten Al Chwarizmi (ca. 783 – 850) leitet sich der Begriff Algorithmus ab. Aus dem Titel eines seiner Werke al-ǧabr wurde der Begriff Algebra abgeleitet. 

Einführendes Beispiel:

Man nehme eine ganze Zahl x, addiere 5 hinzu und verdopple das Ergebnis, um dann davon 7 abzuziehen. Nun ziehe man zweimal die ursprüngliche Zahl ab und addiere wiederum 5.
Weshalb ergibt sich als Ergebnis immer die Zahl 8?

Als Lösung bildet man einen algebraischen Term (Rechenausdruck mit oder ohne Variablen) und vereinfacht ihn schrittweise, hier die Variable x als Stellvertreter für die gedachte Zahl:

(x + 5)٠2 – 7 – 2٠x + 5  =  x٠2 + 5٠2 – 7 – 2٠x + 5 = 2x + 10 – 7 – 2x + 5 =
2x – 2x + 3 + 5 = 8

Bei der Vereinfachung des Terms wurden algebraische Gesetze wiederholt angewendet.

Gesetze der Algebra

Für alle reellen Zahlen (natürliche, ganze Zahlen, Brüche und Wurzeln) a, b, c gilt:

Kommutativ-Gesetz (K-G) der Addition und Multiplikation:

a + b = b + a  und  a٠b = b٠a  

Zur Vereinfachung wird bei der Multiplikation mit Variablen oft auf den Malpunkt verzichtet,  ab = ba  statt  a٠b = b٠a  

Assoziativ-Gesetz (A-G) der Addition und Multiplikation:

(a + b) + c = a + (b + c)  und  (a٠b)٠c = a٠(b٠c) kurz  (a b) c = a (b c)

Distributiv-Gesetze (D-G)

(a + b)٠c = a٠c + b٠c    und   (a – b)٠c = a٠c – b٠c 

(a + b) : c = a : c + b : c  und  (a – b) : c = a : c – b : c 

oder

a٠(b + c) = a٠b + a٠c  und  a٠(b – c) = a٠b – a٠c  (gilt nicht für : )

Bei der Umformung von links nach rechts (bezüglich =) spricht man von Ausmultiplizieren, umgekehrt von Ausklammern.

Vorrangregeln beim Zusammenfassen von Termen:

Punkt(rechnung ٠  : ) vor Strich(rechnung + –)

Was in Klammern steht wird zuerst berechnet.

Gerechnet wird von links nach rechts.

Um beim obigen Beispiel – 2x an die 2. Stelle zu tauschen sind mehrere Schritte notwendig:

   (2x + 3) – 2x + 5 =

= (2x + 3) + (–2x) + 5 =  (Rechenzeichen wird in Vorzeichen umgewandelt)

=  2x + (3 +(–2x)) + 5 =   (A-G)

=  2x + ((–2x) + 3) + 5 =  (K-G)

= (2x +(–2x)) + 3 + 5  =   (A-G)

= 8

Für das Vereinfachen von Termen lässt sich aus den K-, A- und D-Gesetz folgern:

Bei einer Summe dürfen Summanden beliebig vertauscht werden.

Zwei Terme sind gleichwertig (äquivalent), wenn sie durch Anwendung der drei Rechengesetze ineinander umgeformt werden können.

Klammerregeln

a + (b + c) = a + b + c  und  a + (b – c) = a + b – c

Steht ein Plus vor der Klammer, können die Klammern einfach weggelassen werden. 

a – (b + c) = a – b – c  und  a – (b – c) = a – b + c 

Steht ein Minus vor der Klammer, so ändert man beim Weglassen der Klammer das Rechenzeichen in der Klammer.

Multiplizieren von Summen                                  

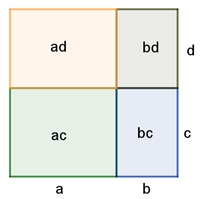
(a + b)(c + d)  = a(c + d) + b(c + d)  =  (D-G)      Veranschaulichung: 

= ac + ad + bc + bd   (D-G)

Schema: =  ac + ad + bc + bd  

Binomische Formeln

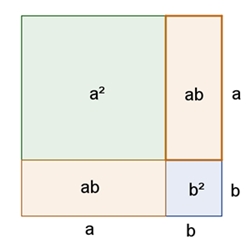
I   (a + b)² = a² + 2ab + b²                                Veranschaulichung  von I:  

II  (a – b)² = a² – 2ab + b²         

III (a + b)(a – b) = a² – b²

Begründungen:

I   (a + b)(a + b) = a² + ab + ba + b² = a² + 2ab + b²

II  (a – b)(a – b) = (a + (–b))(a + (–b)) = a² + (–ab) + (–ba) + b² = a² – 2ab + b²

III (a + b)(a – b) = a² + (–ab) + ba – b² = a² – b²

Die höheren binomischen Formeln und das Pascalsche Dreieck.

 
Rationale Zahlen

Der Quotient zweier ganzer Zahlen a und b oder die Bruchzahl aus a und b bildet eine rationale Zahl:
a : b = a / b  für a, b ϵ ℤ (Menge der ganzen Zahlen).
Die Menge der rationalen Zahlen wird mit ℚ bezeichnet

Bruchzahlen werden durch endliche oder periodische Dezimalzahlen dargestellt.

Beispiele:

7 / 25 = 7٠4 / 25٠4 = 28 / 100 = 0,28  ( 7 / 25 erweitert mit 4 )

3 / 7  =  0,428571 428571 428571 … (6-stellige Periode 428571)

Vorzeichenregeln beim Rechnen mit rationaler Zahlen

Vorzeichenregeln beim Addieren zweier rationaler Zahlen

a) Addieren zweier rationaler Zahlen mit gleichem Vorzeichen

Addiere die Beträge und gib der Summe das gemeinsame Vorzeichen der Summanden

Beispiele:  +7,53 + (+5,39) = +12,92,  kurz:  7,53 + 5,39 = 12,92

                   (–15,23) + (–13,58) = –28,81

b) Addieren zweier rationaler Zahlen mit verschiedenem Vorzeichen

Subtrahiere den kleineren Betrag vom größeren Betrag und gib der Differenz das Vorzeichen des Summanden mit dem größeren Betrag.

Beispiele:  +5,7 + (–3,36) = + (5,70 – 3,36) = 2,34

                   –9,41 + (+5,73) = – (9,41 – 5,73) = –3,68

Vorzeichenregel beim Subtrahieren zweier rationaler Zahlen

Das Subtrahieren einer rationalen Zahl ist gleich bedeutend mit dem Addieren ihrer Gegenzahl,
z.B. Gegenzahl zu 5 ist –5, Gegenzahl zu –3 ist 3

Beispiele:  (– 4,23) – (+3,56) = (– 4,23) + (–3,64) = – 7,87

                     15,34 – (–3,51)  = 15,34 + (+3,51) = 18,85

Vorzeichenregeln beim Multiplizieren bzw. Dividieren zweier rationaler Zahlen

1.  Multipliziere/Dividiere die Beträge.

2.  Bei gleichem Vorzeichen hat das Produkt/Quotient ein  positives Vorzeichen,
     bei verschiedenen Vorzeichen hat das Produkt/Quotient ein  negatives Vorzeichen.

Kurz:      + ٠ +  =  +                    + : +  =  + 
               – ٠ –  =  +                     – : –  =  +
               + ٠ –  =  –                     + : –  =  –             
               – ٠ +  =  –                     – : +  =  –

 
Brüche

Den Quotienten zweier Zahlen z und n kann man auch als Bruch schreiben
                                        
Meist werden für Zähler und Nenner ganze Zahlen verwendet.

Größter gemeinsamer Teiler (ggT)
Gemeinsame Teiler von zwei Zahlen sind die Zahlen, die sowohl Teiler der einen als auch Teiler der anderen Zahl sind. Unter den gemeinsamen Teilern ist die größte Zahl der größte gemeinsame Teiler

Kleinstes gemeinsames Vielfaches (kgV)
Gemeinsame Vielfache von zwei Zahlen sind die Zahlen, die sowohl Vielfache der einen als auch Vielfache der anderen Zahl sind. Unter den gemeinsamen Vielfachen ist die kleinste Zahl das kleinste gemeinsame Vielfache.

Bruchregeln

1. Einen Bruch kürzen bedeutet Zähler und Nenner durch die gleiche Zahl dividieren. Der Wert des Bruches bleibt gleich.
    

2. Einen Bruch erweitern bedeutet Zähler und Nenner mit der gleiche Zahl multiplizieren. Der Wert des Bruches bleibt gleich.   
    =  0,28

3. Brüche gleichnamig machen bedeutet die Nenner durch Erweitern oder Kürzen zur gleichen Zahl umzuformen.
           kgV(8,12) = 24

    Bei gleichnamigen Brüchen hat derjenige Bruch den größeren Wert, dessen Zähler den größeren Wert hat.

4a. Bei der Addition und Subtraktion gleichnamiger Brüche werden die Zähler addiert und der Nenner beibehalten.
       

4b. Bei der Addition und Subtraktion ungleichnamiger Brüche werden die Brüche zuerst gleichnamig gemacht und dann addiert bzw. subtrahiert.
             kgV(6, 8) = 24

5a. Ein Bruch wird mit einer ganzen Zahl multipliziert, indem man den Zähler mit der ganzen Zahl multipliziert und den Nenner beibehält.
                 Kürzen mit 5

5b. Ein Bruch wird durch eine ganze Zahl dividiert, indem man den Zähler beibehält und den Nenner mit der ganzen Zahl multipliziert.
                Kürzen mit 7

5c. Eine ganze Zahl wird durch einen Bruch dividiert, indem man die ganze Zahl mit dem Kehrbruch multipliziert.
                Kürzen mit 8

6a. Zwei Brüche werden multipliziert, indem man die beiden Zähler und die beiden Nenner multipliziert.
             Kürzen mit 5 und 8

6b. Zwei Brüche werden dividiert, indem man den Kehrbruch des zweiten Bruchs multipliziert.
              Kürzen jeweils mit 7

Brüche werden meist gekürzt!

Reelle Zahlen

Definition der reellen Zahlen:

Zahlen, die sich weder durch endliche noch durch periodische Dezimalbrüche (rationale Zahlen) darstellen lassen, heißen irrationale Zahlen.
Rationale und irrationale Zahlen bilden zusammen die Menge der reellen Zahlen ℝ.

Die Vorzeichenregeln sind die gleichen wie bei den rationalen Zahlen.

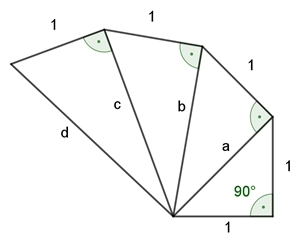
Quadratwurzeln

Definition:
Für a ≥ 0 ist  diejenige nichtnegative Zahl, deren Quadrat a ergibt.
 heißt Quadratwurzel und a heißt Radikant.

  ≈ 1,4142135620  (jeweils gerundet auf 10 Dezimalen)

  ≈ 1,7320508075

  = 2

  ≈ 2,2360679774

 Veranschaulichung mit Hilfe des Satzes von Pythagoras:


a =  , da  a² = 1² + 1²

b =  , da  b² = a² + 1²

c = 2    , da  c² = b² + 1²

d =  , da  d² = c² + 1²

Quadratwurzeln

Für a ϵ ℝ gilt ,  z.B.  .

Für a, b ≥ 0 gilt:

n-te Wurzeln

Die nichtnegative Lösung der Gleichung xⁿ = a mit a ≥ 0 und der natürlichen Zahl n heißt n-te Wurzel von a
                                                                    

Für n-te Wurzeln gelten die entsprechende Multiplikations- und Divisionsregel.

Potenzen

aⁿ = a٠a٠a٠ … ٠a ( n Faktoren a), a heißt Basis und n heißt Exponent (n ϵ ℕ₀).
Speziell: a¹ = a,  a⁰ = 1

Potenzgesetze für natürliche Exponenten m und n und a ≠ 0:

(1)   a^m ٠ aⁿ =  a^m+n  (m + n Faktoren a)

(2a) a^m : aⁿ =  a^m-n  (m – n Faktoren a für m > n)

(2b) aⁿ :  aⁿ  = a⁰ = 1 (für m = n)

(2c) a^m : aⁿ =  1/a^n-m  (n – m Faktoren a für m < n)

(3)   (a^m)ⁿ  =  a^m٠n   (n ٠ m Faktoren a)

Entsprechende Potenzgesetze gelten für rationale Exponenten, wobei gilt: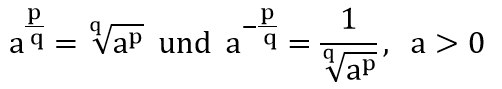

Logarithmen

Die eindeutige Lösung der Eponentialgleichung b^x = a für b > 0, b ≠ 1, a >0 bezeichnet man als Logarithus von a zur Basis b und schreibt x = log_b a.
Bezeichnung für Zehnerlogarithmus:  lg a = log₁₀ a 

Logarithmusgesetze für u > 0, v > 0, a > 0, a ≠ 1

(1)  log_b (u٠v)  =  log_b u + log_b v

(2)  log_b (u : v)  =  log_b u – log_b v

(3)  log_b u^x  =  x٠ log_b u 

Begründungen:

Zu (1):    x = log_b (u٠v) ,  x₁ = log_b u,  x₂ = log_b v 
b^x = u٠v,  b^x1 = u,  b^x2 = v

b^x = u٠v = b^x1 ٠ b^x2 = b^x1+x2  (1. Potenzgesetz)

x = x₁ + x₂  oder  log_b (u٠v)  =  log_b u + log_b v