Geometrie in der Ebene und im Raum

Geometrische Grundbegriffe, Definitionen, Axiome und Sätze der Geometrie mit Beweisen befinden sich bereits im Buch Elemente, in dem Euklid auf Papyrusrollen ca. 300 v. Chr. in Alexandria (Ägypten) das geometrische Wissen seiner Zeit in geordneter Reihenfolge niedergeschrieben hat.
Die Elemente waren lange Zeit Grundlage des Geometrieunterrichts.

Geometrische Grundbegriffe und ebene Geometrie

Eine Gerade wird durch zwei Punkte festgelegt und hat keinen Anfangs- und keinen Endpunkt.

Eine Halbgerade wird durch zwei Punkte festgelegt und hat einen Anfangs- und
keinen Endpunkt

Eine Strecke wird durch zwei Punkte festgelegt und hat einen Anfangs- und
einen Endpunkt.

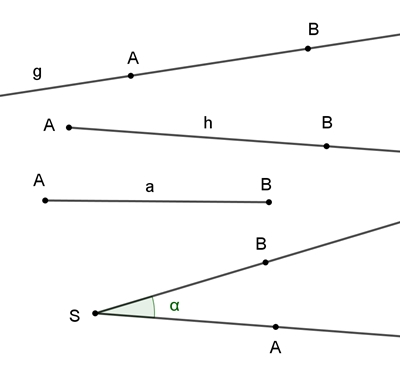
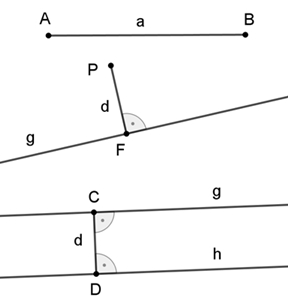
Bezeichnungen:

        Liegt ein Punkt P auf einer Geraden g so schreibt man kurz:  P ϵ g

AB = g    Gerade g durch die Punkte A und B

[AB = h   Halbgerade h mit Anfangspunkt A durch Punkt B

[AB] = a  Strecke a mit Anfangspunkt A und Endpunkt B,  
|AB| = a  oder   = a   Länge a der Strecke [AB] 

(a als Bezeichnung für Strecke als auch für Streckenlänge)

α = ASB  Winkel α zwischen den Halbgeraden [SA und [SB 
S heißt Scheitel des Winkels, [SA und [SB  Schenkel des Winkels α.

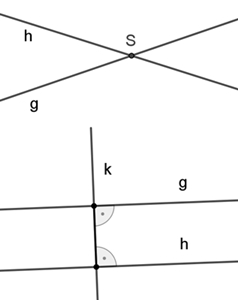
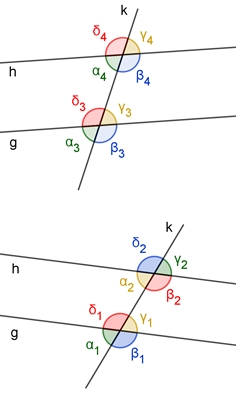
Gegenseitige Lagen zweier Geraden

a) Zwei Geraden g und h schneiden sich im Punkt S,
    kurz: g ∩ h = {S},
    Sonderfall:  g ist senkrecht zu h, kurz:  g ⊥ h

b) Zwei Geraden g und h sind zueinander parallel,
    wenn eine dritte Gerade k senkrecht zu den
    beiden Geraden g und h ist.

Scheitelwinkel und Nebenwinkel

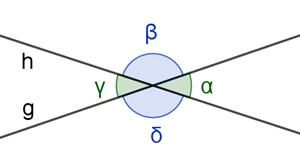
    Scheitelwinkel sind zwei gegenüberliegende Winkel an einer Geradenkreuzung.
   Sie sind gleich groß, α = γ   und  β = δ
   Nebenwinkel ergänzen sich zu 180°, α + β = 180°,
   β + γ = 180°, γ + δ = 180° und δ + α = 180°

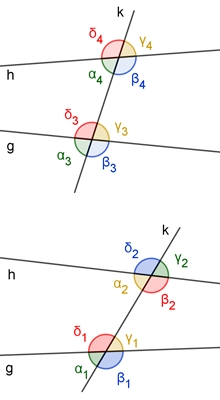
Stufenwinkel und Wechselwinkel

    Die gleich gefärbten Winkel heißen Stufenwinkel.

       Die gleich gefärbten Winkel heißen Wechselwinkel.

Stufenwinkel und Wechselwinkel an parallelen Geraden

Wenn g und h parallel sind, dann sind Stufenwinkel und Wechselwinkel gleich groß.

Umgekehrt gilt:

Wenn Stufenwinkel oder Wechselwinkel gleich groß sind, dann sind die Geraden g und h zueinander parallel.

Abstände

Abstand der Punkte A und B:  a = |AB|

Abstand des Punktes P von der Geraden g:
Länge der zu g senkrechten Verbindungstrecke (Lot)
d = |PF|

Abstand der Geraden g und h:
Länge der zu g und h senkrechten Verbindungsstrecke
d = |CD|

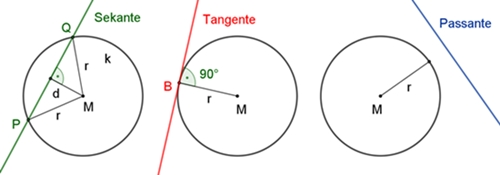
Kreis und Gerade  (Sekante, Tangente und Passante)

Die Sekante schneidet den Kreis k in zwei Punkten.  Der Abstand d der Sekante vom Mittelpunkt M des Kreises k ist kleiner als der
Radius r.

Die Tangente berührt den Kreis im Punkt B. Die Tangente bildet mit der Strecke BM einen rechten Winkel. Der Abstand der Tangente vom Mittelpunkt ist gleich dem Radius r.

Die Passante verläuft außerhalb des Kreises. Der Abstand der Passante vom Mittelpunkt des Kreises ist größer als der Radius.

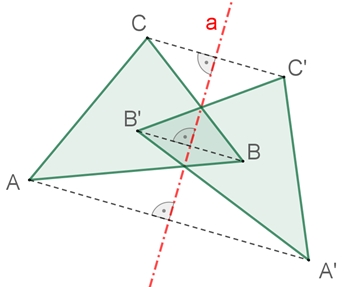
Symmetrien

Achsensymmetrie

 Die Verbindungsstrecke zweier zueinander achsensymmetrischer Punkte wird von der Symmetrieachse a halbiert und steht auf dieser senkrecht.

Liegt ein Punkt auf der Achse, so stimmt er mit seinem Spiegelpunkt überein.

Dreieck A´B´C´ und Dreieck ABC sind zueinander kongruent, d.h. entsprechende Strecken sind gleich lang, entsprechende Winkel sind gleich groß, die Flächeninhalte sind gleich groß. Der Umlaufsinn des gespiegelten Dreiecks ändert sich.

Punktsymmetrie

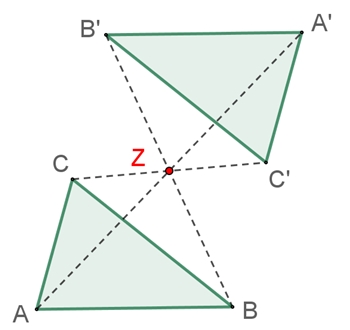
Die Verbindungsstrecke zweier zueinander punktsymmetrischer Punkte wird vom Symmetriezentrum Z halbiert.

Dreieck A´B´C´ und Dreieck ABC sind zueinander kongruent, d.h. entsprechende Strecken sind gleich lang, entsprechende Winkel sind gleich groß, die Flächeninhalte sind gleich groß.

Der Umlaufsinn des punktgespiegelten Dreiecks bleibt gleich.
Punktsymmetrische Geraden sind parallel.

Rotationssymmetrie (Drehsymmetrie)

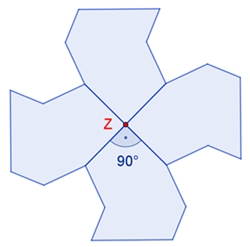
Eine Figur ist n-fach rotationssymmetrisch, wenn sie bei einer Drehung um das Drehzentrum Z um den Winkel φ = 360°/n (n natürliche Zahl) ein erstes Mal auf sich selbst abgebildet wird.
Eine 2-fache Rotationssymmetrie entspricht einer Punktspiegelung.

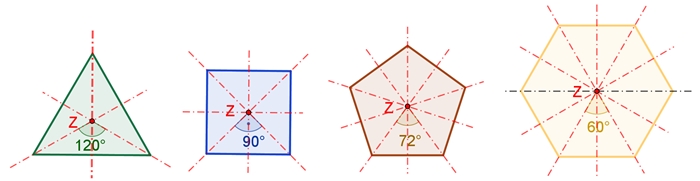
1. Beispiel: regelmäßige Vielecke mit rot gekennzeichneten Symmetrieachsen

Gleichseitiges Dreieck:  3-fach rotationssymmetrisch, φ = 360°/3 = 120°

Quadrat:                         4-fach rotationssymmetrisch, φ = 360°/4 = 90°

Regelmäßiges Fünfeck:  5-fach rotationssymmetrisch, φ = 360°/5 = 72°

Regelmäßiges Sechseck: 6-fach rotationssymmetrisch, φ = 360°/6 = 60°

2. Beispiel:  4-fach rotationssymmetrische Figur ohne Symmetrieachse

 Vielecke, Eigenschaften und Flächeninhalte

a) Das Rechteck

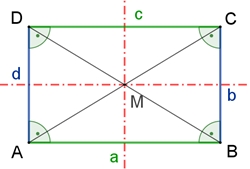
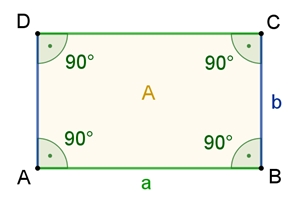
Ein Rechteck ist ein Viereck mit vier rechten (90°) Innenwinkeln.

Eigenschaften des Rechtecks ABCD:

I    Gegenüberliegende Seiten sind parallel und gleich lang, a = c und b = d.

II   Die beiden Diagonalen sind gleich lang und schneiden sich im Mittelpunkt M des Rechtecks.

III  Das Rechteck hat zwei zueinander senkrechte Symmetrieachsen durch den Mittelpunkt M;
     das Rechteck ist auch punktsymmetrisch mit Symmetriezentrum M.

 Sonderfall: Quadrat

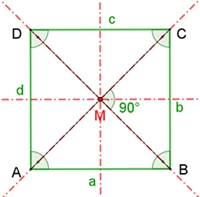
I    Alle vier Seiten sind gleich lang, a = b = c = d

II   Die Diagonalen schneiden sich senkrecht

III  Das Quadrat hat 4 Symmetrieachsen durch den Mittelpunkt M, ist punktsymmetrisch
     zum Symmetriezentrum M und hat eine 4-fache Rotationssymmetrie.

Flächeninhalt des Rechtecks

Der Flächeninhalt eines Rechtecks ABCD mit der Länge a und der Breite b ist A = a٠b

Sonderfall: Quadrat b = a
Flächeninhalt des Quadrats A = a٠a = a² 

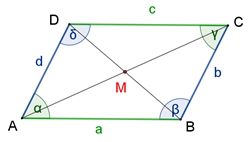
b) Das Parallelogramm

Ein Parallelogramm ist ein Viereck mit jeweils zwei gegenüberliegenden parallelen Seiten.

      Eigenschaften des Parallelogramms ABCD:

I    Gegenüberliegende Seiten sind gleich lang, a = c und b = d.

II   Gegenüberliegende Winkel sind gleich groß,  α = γ  und  β = δ.

III  Das Parallelogramm ist punktsymmetrisch zum Symmetriezentrum M.

        Sonderfall: Raute a = b = c = d

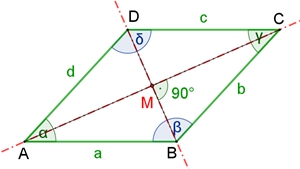
I   Alle vier Seiten sind gleich lang, a = b = c = d

II  Die Diagonalen halbieren sich senkrecht.

III Die Raute besitzt zwei Symmetrieachsen durch den Mittelpunkt und ist punktsymmetrisch
      zum Symmetriezentrum M.

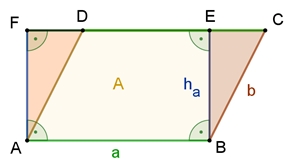
 Flächeninhalt des Parallelogramms

Der Flächeninhalt des Parallelogramms ABCD beträgt A = a٠h_a.

Dreieck BCE parallel verschoben und an [AB] angesetzt liefert ein flächengleiches Rechteck mit den Seiten a und h_a.

c)  Das Dreieck

siehe Lehrsätze im Dreieck,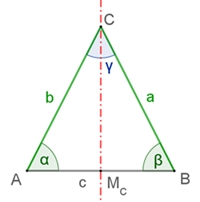

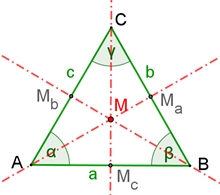
Sonderfälle: gleichschenkliges Dreieck, gleichseitiges Dreieck

Gleichschenkliges Dreieck ABC, a = b

I    Die beiden Basiswinkel sind gleich groß, α = β.

II   Es besitzt eine Symmetrieachse durch Mc und C.

Gleichseitiges Dreieck ABC,  a = b = c

I   Alle Winkel sind gleich groß, α = β = γ = 60°.

II  Es besitzt drei Symmetrieachsen durch den Mittelpunkt und hat eine 3-fache Rotationssymmetrie.

Flächeninhalt des Dreiecks:

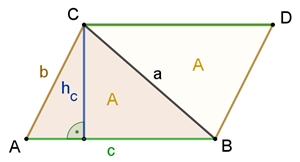
Der Flächeninhalt des Dreiecks ABC beträgt A = ½٠c٠h_c.

Durch die Strecke [BC] wird das Parallelogramm ABDC in 2 gleichgroße (kongruente) Dreiecke unterteilt.

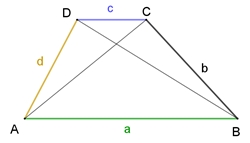
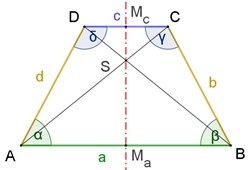
d)  Das Trapez

Ein Trapez ist ein Viereck mit zwei parallelen Seiten.

Sonderfall: gleichschenkliges Trapez

Eigenschaften des Trapezes ABCD:

I   Basisschenkel sind gleich lang, b = d,

II  Basiswinkel sind gleich groß, α = β  und γ = δ

III Das gleichschenklige Trapez besitzt eine Symmetrieachse durch M_a, S und M_c

Flächeninhalt vom Trapez

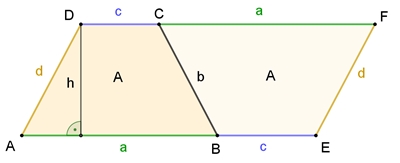
Der Flächeninhalt des Trapezes ABCD beträgt A = ½٠(a+b)٠ h 

Das Parallelogramm AEFD wird durch die Strecke [BC] in 2 gleichgroße Trapeze unterteilt.

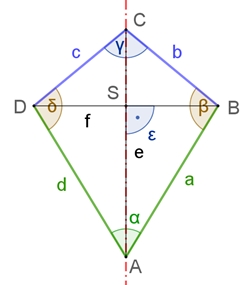
e)  Das Drachenviereck

Ein Drachenviereck ist ein Viereck, das zwei Paare gleich langer benachbarter Seiten besitzt.

Eigenschaften des Drachenvierecks ABCD:

I   Zwei gegenüberliegende Winkel sind gleich groß.

II  Die Diagonalen schneiden sich senkrecht

III Das Drachenviereck besitzt eine Symmetrieachse durch A, S und C.

   
       Flächeninhalt vom Drachenviereck

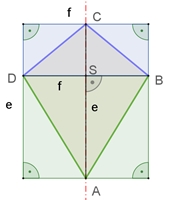
Der Flächeninhalt des Drachenvierecks ABCD beträgt A = ½٠e٠f

Das Drachenviereck hat den halben Flächeninhalt eines umschließenden Rechtecks mit dem
Flächeninhalt  e٠f. 

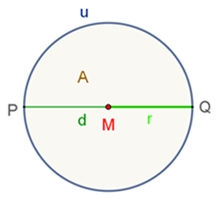
f)  Der Kreis

Die Kreiszahl π ist festgelegt durch den Quotienten aus Kreisumfang u und Kreisdurchmesser d,  π = u : d.  Daraus folgt:

  Kreisumfang u:             u = d٠π = 2٠r٠π

  Kreisflächeninhalt A:   A = r²٠π

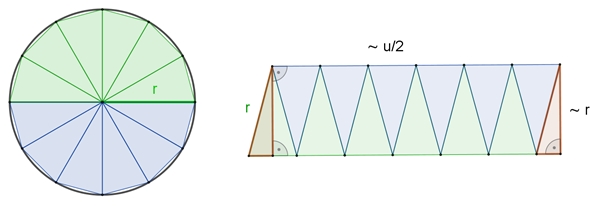
Begründung:

Die Kreisfläche wird durch ein eingepasstes reguläres n-Eck in gleich große Dreiecke unterteilt und passend zu einem Rechteck zusammengesetzt. Je größer die Eckenzahl n ist, umso mehr nähert sich die Rechtecklänge dem halben Umfang u/2 an und die Rechteckbreite dem Radius r an.
Im Grenzfall stimmt der Inhalt der Kreisflächen mit dem Inhalt der Rechteckfläche überein. Daraus folgt:

Kreisflächeninhalt A = u/2٠r = 2rπ : 2٠r = r²π

Kreissektor

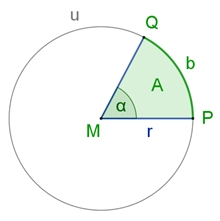
Es gelten folgende Proportionen mit u = 2rπ:
b : 2rπ  =  α : 360°  und  A : r²π =  α : 360° 

Daraus folgt:
Länge des Kreisbogens              b = α : 360°٠2rπ
Flächeninhalt des Kreissektors  A = α : 360°٠r²π

Raumgeometrie

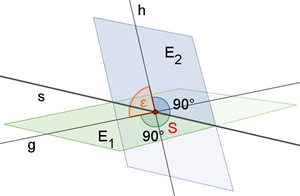
Geraden und Ebenen im Raum

Definitionen:

Eine Gerade s heißt Senkrechte oder Lot zur Ebene E, wenn sie mit zwei sich in S schneidenden Geraden g und h dieser Ebene einen rechten Winkel bildet.

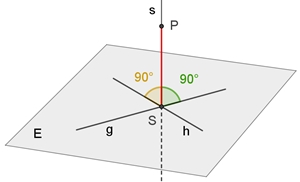
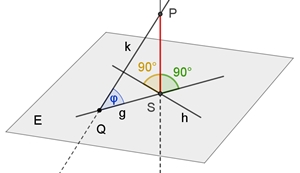
Die Länge der Lotstrecke [PS] ist der Abstand des Punktes P von der Ebene E.

Der Neigungswinkel φ einer Geraden k gegen die Ebene E ist der  PQS des rechtwinkligen Dreiecks QSP. Q ist der Schnittpunkt der Geraden k mit der Ebene E und S der Fußpunkt des Lotes von P auf E.

Schneiden sich zwei Ebenen E₁ und E₂ in einer Geraden s, so nennt man den spitzen Winkel zwischen zwei sich in S schneidenden Geraden g und h, die jeweils auf s senkrecht stehen und in der Ebene E₁ und E₂ liegen, den Neigungswinkel ε zwischen den Ebenen E₁ und E₂.

Beispiel:  Bestimmung des Neigungswinkels der Raumdiagonalen im Quader
Die Seitenflächen des Quaders sind jeweils zwei gleich große gegenüberliegende Rechtecke.

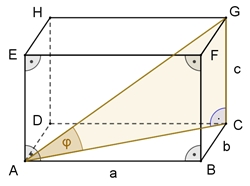
Um den Neigungswinkel φ = CAG in wahrer Größe zu konstruieren, muss zunächst das rechtwinklige Dreieck ABC in wahrer Größe und dann das rechtwinklige Dreieck ACG gezeichnet werden.
Bei der Berechnung des Winkels φ wendet man zweimal den Satz des Pythagoras an:

|AC|² = a² + b²  und  |AG|² = |AC|² + c². Daraus folgt: |AG|² = a² + b² + c²
                                

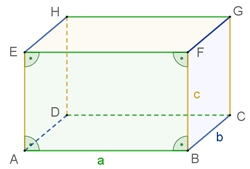
Volumen- und Oberflächeninhalt des Quaders

Für den Quader mit der Grundfläche G = a٠b und der Höhe h = c gilt:

Volumeninhalt:       V = G٠h = abc

Oberflächeninhalt:  O = 2ab + 2ac + 2bc

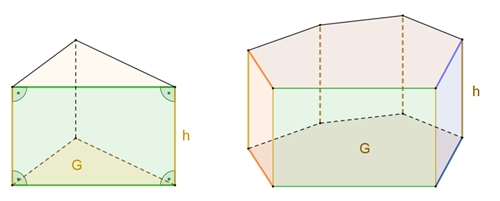
Volumen- und Oberflächeninhalt des geraden Prismas

Wird ein Vieleck als Grundfläche senkrecht um h nach oben verschoben, so entsteht ein Körper mit Rechtecken als Seitenflächen und einer zur Grundfläche G gleich großen Deckfläche. Dieser Körper heißt gerades Prisma.
Die Mantelfläche M ist die Summe aller Seitenflächen.

Volumeninhalt:       V = G٠h

Oberflächeninhalt:  O = 2G + M

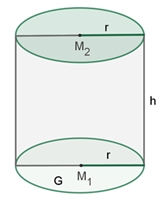
Volumen- und Oberflächeninhalt des geraden Zylinders

Wird eine Kreisfläche (Kreisradius r) als Grundfläche senkrecht um h nach oben verschoben, so entsteht als Körper ein gerader Zylinder mit einer zur Grundfläche G gleich großen Kreisfläche als Deckfläche. Die Mantelfläche M des geraden Zylinders ist ein Rechteck.

Volumeninhalt:           V = G٠h = r² π h

Mantelflächeninhalt:  M = 2 r π h

Oberflächeninhalt:      O = 2 G + M

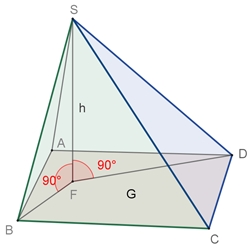
Volumen- und Oberflächeninhalt der Pyramide

Eine Pyramide ist ein geometrischer Körper, dessen Grundfläche ein Vieleck ist und dessen Seitenflächen Dreiecke mit einer gemeinsamen Spitze S sind.

Eine Pyramide, deren Grundfläche ein gleichseitiges Dreieck ist und deren Seitenflächen zur Grundfläche kongruente Dreiecke sind, nennt man reguläres  Tetraeder.

Eine Pyramide, deren Grundfläche ein Quadrat ist und deren Pyramidenspitze senkrecht über dem Mittelpunkt des Quadrats liegt, heißt quadratische Pyramide.

Eine Pyramide, deren Grundfläche ein regelmäßiges Vieleck ist und deren Pyramidenspitze senkrecht über dem Mittelpunkt des Vielecks liegt, heißt reguläre Pyramide. Ihre Seitenflächen sind kongruente gleichschenklige Dreiecke.

Die Höhe h der Pyramide ist die Verbindungsstrecke von Spitze und Fußpunkt des Lotes von S auf die Grundfläche G.

Volumeninhalt:          V = 1/3٠G٠h

Mantelflächeninhalt: M = Summe aller Dreiecksflächeninhalte (ohne Grundfläche)

Oberflächeninhalt:     O = G + M

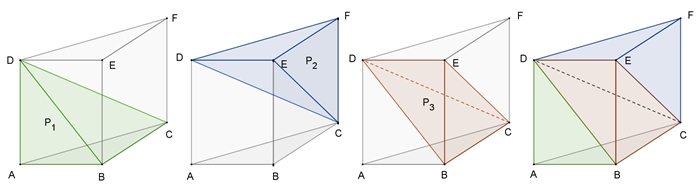
Begründung der Formel für V für eine dreiseitige Pyramide mit Hilfe des Satzes (Prinzips) von Cavalieri.

Zwei Körper besitzen denselben Volumeninhalt, wenn alle ihre Schnittflächen in Ebenen parallel zur Grundebene in gleichen Höhen denselben Flächeninhalt haben.

Aus ihm folgt, dass Pyramiden mit gleicher Grundfläche und gleicher Höhe den gleichen Volumeninhalt besitzen.

Die beiden Pyramiden P₁ und P₂ haben den gleichen Volumeninhalt, da sie kongruente Grundflächen ABC und DEF sowie gleiche Höhen |AD| = |CF| besitzen.
Die Pyramiden P₂ und P₃ haben den gleichen Volumeninhalt, da sie kongruente Grundflächen CFE und EBC sowie die gemeinsame Höhe [DE] besitzen.
Dann müssen aber alle drei Pyramiden den gleichen Volumeninhalt besitzen.
Daraus folgt für den Volumeninhalt einer Pyramide: V = 1/3٠G٠h

Volumen- und Oberflächeninhalt des geraden Kreiskegels

Die Grundfläche des Kreiskegels ist eine Kreisfläche. Die Spitze des geraden Kreiskegels befindet sich senkrecht über dem Kreismittelpunkt. Die Verbindungslinien von Kegelspitze und Kreislinie heißen Mantellinien.

Netz des Kreiskegels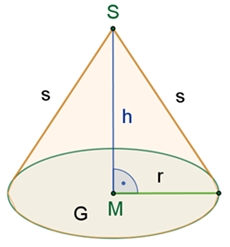

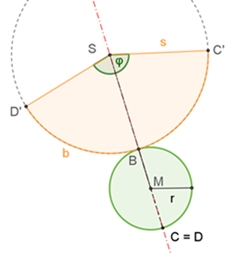
Die Bogenlänge b des Kreissektors mit Mittelpunktswinkel φ entspricht dem Kreisumfang 2 r π der kreisförmigen Grundfläche, b = 2 r π.
 
           

φ : 360° = (2rπ) : (2sπ)
(1)  φ : 360° = r : s
(2)  φ : 360° = M : (s²π)

(1) = (2):

M : (s²π) = r : s
M = r : s ٠ (s²π)
M = r٠s٠π

Man nähert den Kreis der Grundfläche durch ein reguläres n-Eck mit zunehmend größerem n an. Dann nähert sich die Fläche des n-Ecks der Kreisfläche. Daher ist es naheliegend, dass für den Kreiskegel die gleiche Formel für den Volumeninhalt wie bei der Pyramide gilt:

Volumeninhalt:           V = 1/3٠G٠h = 1/3 r²π h

Mantelflächeninhalt:  M = r s π

Oberflächeninhalt:      O = G + M = r²π + r s π

Volumen- und Oberflächeninhalt der Kugel

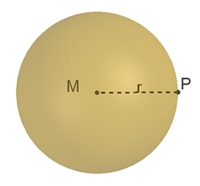
Kugelradius r

Volumeninhalt        V = 4/3 r³π

Oberflächeninhalt   O = 4 r²π

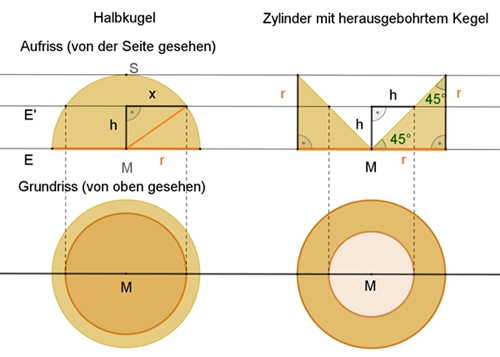
Begründung für Volumeninhalt:

Eine Halbkugel und ein gleichhoher Zylinder mit herausgebohrtem Kegel (Vergleichskörper) stehen auf einer Ebene E und werden von einer dazu parallelen Ebene E´ in den Schnittflächen A_Kreis und A_Kreisring geschnitten.

A_Kreis = x²π  mit x² + h² = r² oder x² = r² – h²  
A_Kreis = (r² – h²) π 
A_Kreisring = r²π – h²π = (r² – h²) π 
⇒ A_Kreis = A_Kreisring, Halbkugel und Vergleichskörper haben in jeder Schnitthöhe inhaltsgleiche Querschnittsflächen und mit dem Satz von Cavalieri folgt dann ihre Volumengleichheit.
V_Halbkugel = V_{Vergleichskörper} = V_Zylinder – V_Kegel  =  r² π r – 1/3 r² π r  =  2/3 r³ π

Daraus folgt für den Volumeninhalt der Kugel  V = 4/3 r³ π

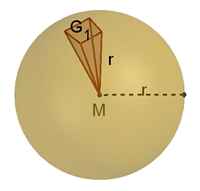
Begründung für Oberflächeninhalt:

Man stellt sich die Kugel in eine Reihe von n Pyramiden zerlegt vor, deren Spitzen sich in M befinden und deren Grundflächen G_n die Kugeloberfläche berühren.
Dann gilt für den Volumeninhalt V´ und den Oberflächeninhalt O´ des aus n Pyramiden zusammengesetzten Körpers:

V´ =  1/3٠(G₁ + G₂ + G₃ + … + G_n)٠r,  r ≈ h
O´ =  G₁ + G₂ + G₃ + … + G_n
⇒  O´ = 3/r٠V´

Wird n zunehmend größer, so nähert sich h dem Radius r und O´ dem Oberflächeninhalt der Kugel immer genauer an.

 ⇒  O = 3/r٠V = 3/r٠4/3٠r³π  =  4 r²π