Grundlegende Konstruktionen

Bei Konstruktionen im klassischen Sinn wird nur Zirkel und Lineal verwendet.
Mit Hilfe von Geometriesoftware w.z.B. geogebra können Konstruktionen am Computer erfolgen.

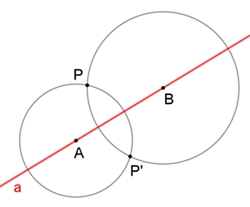
Zwei Kreise mit beliebigen Mittelpunkten A und B auf a durch den Punkt P liefert als zweiten Schnittpunkt den Spiegelpunkt P´ zu P.

2. Konstruktion der Symmetrieachse zu zwei Punkten A und B
    oder Konstruktion der Mittelsenkrechten zu zwei Punkten A und B

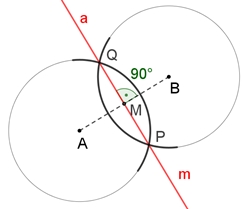
Zwei sich schneidende gleich große Kreise um A und B
liefern zwei Schnittpunkte P und Q durch die die Symmetrieachse a festgelegt ist.

Mit dieser Konstruktion erhält man auch die Mittelsenkrechte m der Punkte A und B.

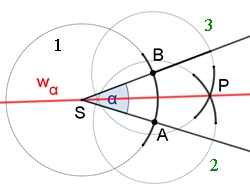
3. Konstruktion der Winkelhalbierenden

Die Winkelhalbierende w_α ist die Symmetrieachse der beiden Schenkeln des Winkels.
1:  Beliebiger Kreis um S schneidet die Schenkel in A und B.
2:  Der Kreis um A ist so gewählt, dass sich ein gleich großer Kreis um B (3) mit dem
     Kreis um A in einem Punkt P schneidet.
       w_α geht durch S und P.

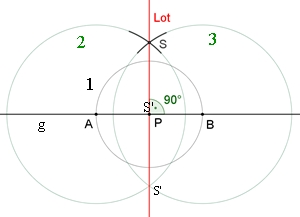
4. Konstruktion des Lotes vom Punkt P der Geraden zur Geraden g
    oder Konstruktion des rechten Winkels
    bzw. im Punkt P wird das Lot zu g errichtet.

1:  Um P wird ein Kreis gezeichnet, der die Gerade g in den Punkten A und B schneidet.

2-3:  Um A und B werden zwei gleich große Kreise gezeichnet, die sich in einem Punkt S schneiden.

Das Lot ist die Gerade, die durch die Punkte P und S (bzw. S´) festgelegt ist.

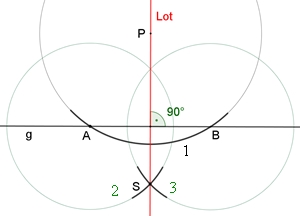
5. Konstruktion des Lotes von einem Punkt P zu einer Geraden g
    bzw. vom Punkt P wird das Lot auf g gefällt.

1:  Um P wird ein Kreis gezeichnet, der die Gerade g in den Punkten A und B schneidet

2-3:  Um A und B werden zwei gleich große Kreise gezeichnet, die sich in einem Punkt S schneiden

Das Lot ist die Gerade, die durch die Punkte P und S festgelegt ist.

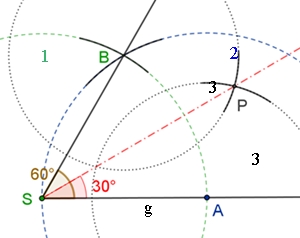
6. Konstruktion spezieller Winkel

a)  90°- und 45°-Winkel s. Konstruktion 4) und 3)

b)  60°- und 30°-Winkel

    1:  Kreis k₁ um S mit beliebigem Radius r.  g ∩ k₁ = {A}

    2:  Kreis k₂ um A mit demselben Radius r.  k₁ ∩ k₂ = {B}, [SB ist der 2. Schenkel des Winkels 60°.

    3:  Kreise um A und B mit gleichem Radius liefert den Schnittpunkt P der Winkelhalbierenden.

Begründung:
Δ SAB ist ein gleichseitiges Dreieck, bei dem alle Innenwinkel gleich groß und damit 60° sind.

Der 30°-Winkel ergibt sich durch Konstruktion der Winkelhalbierenden des 60°-Winkels.