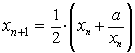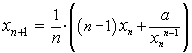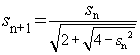Programmbeispiele zur Programmiersprache Python 

Die Programmeingabe erfolgt jeweils nach Aufruf von IDLE (Python GUI) in New Window (Strg+N).

Die Programmausführung mit Python Version 3.6.0 erfolgt dann nach Speicherung des Programms mit Run Module (F5).  

1. Beispiel:

Näherungsweise Berechnung der Quadratwurzel von a mit Hilfe der Iterationsformel   

(Formel von Heron) und dem Startwert x₁.

Programm:

# wurzel.py

a = float(input("Zu berechnende Quadratwurzel: "))

x = float(input("Startwert x1: "))

# float bedeutet, dass mit Kommazahlen gerechnet werden soll!  

print ("Iteration  Näherungswert")

print ("_________________________")   

for i in range(1,6):

  x = 0.5*(x+a/x)

  print ('   ',i,'    ',x)

Ausgabe:

Zu berechnende Quadratwurzel: 2

Startwert x1: 1

Iteration  Näherungswert

_________________________

    1      1.5

    2      1.4166666666666665

    3      1.4142156862745097

    4      1.4142135623746899

    5      1.414213562373095

2. Beispiel:

Näherungsweise Berechnung der n-ten Wurzel von a   mit Hilfe der Iterationsformel 

und dem Startwert x₁.

Programm:

# wurzel_n.py

a = float(input("Zu berechnende n.Wurzel: "))

n = float(input("Eingabe von n: "))

x = float(input("Schätzwert: "))  

print ("Iteration  Näherungswert")

print ("______________________________")   

for i in range(1,6):

  x = ((n-1)*x+a/(x**(n-1)))/n

  #  Bemerkung: x**(n-1) bedeutet x hoch n-1

  print ('   ',i,'    ',x)

Ausgabe:

Zu berechnende n-te Wurzel: 10

Eingabe von n: 4

Schätzwert: 2

Iteration  Näherungswert

______________________________

    1      1.8125

    2      1.7792364129320595

    3      1.7782801818808485

    4      1.7782794100394252

    5      1.7782794100389228

3. Beispiel:

Simulation eines Münzwurfes.

Programm:

# muenze.py

# muenze_werfen

from random import randrange            # Aus dem Modul random wird

m = int(input("Anzahl der Versuche: ")) # der Befehl randrange

n = 1                                   # geladen

k = m

print

print ('         n       hn(Z)')

print ('_________________________')

while n<m:

  z = 0

  n = 10*n

  k = k / 10

  for i in range(1,n+1):

     if randrange(1,3) == 1: # Erzeugen der Zufallszahl 1 oder 2

        z = z+1

  print ((10-len(str(n)))*' ',n,'   ',float(z)/n)    
  # 10 – Länge der Zeichenkette von n

  # oder:  print ("%10i %14f" % (n, float(z)/n))

Ausgabe:

Anzahl der Versuche: 1000000

         n       hn(Z)

_________________________

         10     0.6

        100     0.52

       1000     0.522

      10000     0.5094

     100000     0.49642

    1000000     0.500504

4. Beispiel:

Lösungen einer quadratischen Gleichung der Form  ax² + bx + c = 0.
Lösungsterm:       

Programm:

# quadr_gleich.py

from math import sqrt   #  sqrt() ist die Quadratwurzelfunktion

print "Quadratische Gleichung mit den \nKoeffizienten a, b und c lösen."

a = float(input("a eingeben: "))        # \n bedeutet: neue Zeile

b = float(input("b eingeben: "))

c = float(input("c eingeben: "))

d = b*b-4*a*c

if d > 0:

   x1 = (-b - sqrt(d))/(2*a)

   x2 = (-b + sqrt(d))/(2*a)

   print ("Die Gleichung hat die beiden Lösungen:")

   print ('x1 =',x1,'; x2 =',x2)

elif d == 0:

   x1 = (-b)/(2*a);

   print ("Die Gleichung hat die Lösung:")

   print ('x =',x1)

else:

   print ("Die Gleichung hat keine Lösung!")

Ausgabe:

Quadratische Gleichung mit den

Koeffizienten a, b und c lösen.

a eingeben: 2

b eingeben: 5

c eingeben: 3

Die Gleichung hat die beiden Lösungen:

x1 = -1.5 ; x2 = -1.0
 

5. Beispiel:

Näherungsweise Berechnung der Kreiszahl p. Iterationsterm: 

Programm:

# pi-berechn1.py

# pi-Berechnung mit regulären 2n-Ecken

from math import sqrt, pi

n = 6    # Start mit regelmäßigem Sechseck

s = 1    # Seitenlänge des reg. Sechsecks

print ("Schrittweise Näherung von pi mit Hilfe eines 2n-Ecks")

for i in range(1,31):

    pi_naeherung = 0.5*n*s

    print (round(pi_naeherung,11))

    s = sqrt(2-sqrt(4-s*s))

    n = 2*n  # doppelte Eckenzahl

print ("Ungeeignete Iteration!")

print ("pi =",round(pi,11))

Ausgabe:

Schrittweise Näherung von pi mit Hilfe eines 2n-Ecks

3.0

3.10582854123      

3.13262861328

3.13935020305

3.14103195089

3.14145247229

3.14155760791

3.14158389215

3.14159046324

3.14159210604

3.14159251659

3.14159261864

3.14159264532

3.14159264532

3.14159264532

3.14159264532

3.14159366985

3.14159230381

3.14160869622

3.14158683966

3.14167426502

3.14167426502

3.14307274017

3.15980616494

3.18198051534

3.35410196625

4.24264068712

6.0

0.0

0.0

Ungeeignete Iteration!

pi = 3.14159265359
 

6. Beispiel:

Näherungsweise Berechnung der Kreiszahl p. Iterationsterm:  

Programm:

# pi-berechn2.py

# pi-Berechnung mit regulären 2n-Ecken

from math import sqrt, pi

n = 6  # Start mit regulärem Sechseck

s = 1  # Seitenlänge des reg. Sechsecks

print ("Schrittweise Näherung von pi mit Hilfe eines 2n-Ecks")

for i in range(1,21):

    pi_naeherung = 0.5*n*s

    print (round(pi_naeherung,11))

    s = s/sqrt(2+sqrt(4-s*s))

    n = 2*n  # doppelte Eckenzahl

print ("Gute Iteration!")

print ("pi =",round(pi,11))

Ausgabe:

Schrittweise Näherung von pi mit Hilfe eines 2n-Ecks

3.0

3.10582854123             

3.13262861328

3.13935020305

3.14103195089

3.14145247229

3.14155760791

3.14158389215

3.14159046323

3.141592106

3.14159251669

3.14159261937

3.14159264503

3.14159265145

3.14159265306

3.14159265346

3.14159265356

3.14159265358

3.14159265359

3.14159265359

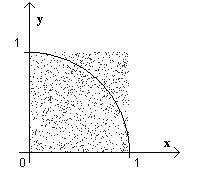
Gute Iteration!  

pi = 3.14159265359

7. Beispiel:

Näherungsweise Berechnung der Kreiszahl p mit der Methode von Monte Carlo.

Es werden in einem Quadrat Zufallszahlen für die x- und y-Koordinate eines Punktes zwischen 0 und 1 erzeugt. Dann wird gezählt, wie viele Punkte davon in einen Viertelkreis fallen. Das Verhältnis Anzahl der Punkte im Viertelkreis zu Anzahl der Punkte insgesamt multipliziert mit der Zahl 4 liefert etwa die Kreiszahl  p. Die Näherung für p ist um so besser, je mehr Zufallspunkte erzeugt worden sind. 

Programm:

# pi-monte_carlo.py

# pi-Bestimmung mit der Methode von Monte Carlo

from random import random

print ("Monte Carlo Methode zur")

print ("Näherung für pi:")

g = int(input("Gesamtzahl der Tropfen: "))

v = 0

x=0; y=0  # Koordinaten des Punktes P

for i in range(1,g+1): 

      x = random()

      y = random()

      if x*x+y*y<= 1:  

         v = v + 1 

pi_naeh = 4.0*v/g

print (g,"Tropfen, davon",v,"Tropfen im Viertelkreis,")

print ("pi etwa",pi_naeh)

Ausgabe:

Monte Carlo Methode zur

Näherung für pi:

Gesamtzahl der Tropfen: 1000000

1000000 Tropfen, davon 785252 Tropfen im Viertelkreis,

pi etwa 3.141008

8. Beispiel:

Potenzen von 0,3  und deren Summen.

Programm:

# potenz-1_3.py

# Potenzen von 1/3 und deren Summe

n = int(input("Bis zu welcher Potenz von 1/3? "))

i = 1

potenz = 1.0/3

print ()

print ('  i      1/3^i       Summe')

print ('-------------------------------')

sum_potenz = potenz

while i<=n:

    print ('%3d   %1.8f   %1.8f' % (i,potenz, sum_potenz))

    i = i+1

    potenz = (1.0/3)**i

    sum_potenz = sum_potenz+potenz

Ausgabe:

Bis zu welcher Potenz von 1/3? 15

  i      1/3^i       Summe

-------------------------------

  1   0.33333333   0.33333333

  2   0.11111111   0.44444444

  3   0.03703704   0.48148148

  4   0.01234568   0.49382716

  5   0.00411523   0.49794239

  6   0.00137174   0.49931413

  7   0.00045725   0.49977138

  8   0.00015242   0.49992379

  9   0.00005081   0.49997460

 10   0.00001694   0.49999153

 11   0.00000565   0.49999718

 12   0.00000188   0.49999906

 13   0.00000063   0.49999969

 14   0.00000021   0.49999990

 15   0.00000007   0.49999997

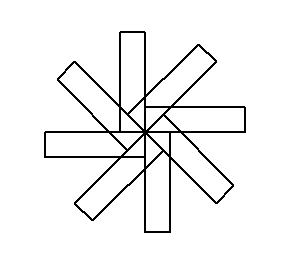
9. Beispiel:

Zeichnen mit Hilfe der Turtle (Schildkröte)                                         

Programm:

# windrad.py
from turtle import *
color('black')

pendown()

hideturtle()

def rechteck(seite): # Prozedur rechteck wird definiert
    for i in [1,2]:
        forward(seite); left(90)
        forward(seite/4); left(90)

speed(0) # maximale Zeichengeschwindigkeit
width(2) # Zeichenstiftbreite
for i in range(1,9):
    rechteck(100)
    left(45)

Ausgabe:
                 

10. Beispiel:

Parkettierung mit Hilfe der Turtle (Schildkröte)                                         

Programm:

# parkett.py

from turtle import * 

def raute(laenge, winkel, strich_dicke, col):

    width(strich_dicke)

    color(col)

    for i in range (1,3):

       forward (laenge); left(winkel)

       forward (laenge); left(180-winkel) 

speed(0)

anzahl_reihe = 10

up(); backward(280); left(90); forward(220); right(90); down()

for i in range(1,15):

  for j in range(1,anzahl_reihe+1):

    raute(50, 45, 1, 'darkgreen')

    up(); forward(50); down()

  up(); backward(anzahl_reihe*50); right(90); forward(35); left(90); down()

Ausgabe:

11. Beispiel:

Wald aus zufällig stehenden Bäumen                                  

Programm:

# baeume.py

# Wald mit Bäumen

from turtle import *

from random import random

def baum(a):

   for i in range(1,3):

       color("brown")

       begin_fill()

       forward(a); left(90)

       forward(2*a); left(90)

       end_fill()

   up(); left(90); forward(2*a); left(90); forward(a); left(180); down()

   color("darkgreen")

   begin_fill()

   forward(3*a); left(110)

   forward(4.39*a); left(140); forward(4.39*a); left(110)

   end_fill()

   up(); forward(a); right(90); forward(2*a); left(90); down()

speed(0)      # max. Zeichengeschwindigkeit

up(); backward(220); left(90); forward(220); right(90); down()

# Turtle im Windwows-Fenster nach links oben setzen

a=8 # Breite Baumstamm

anzahl_x = 12  # Anzahl der Bäume in x-Richtung

anzahl_y = 8   # Anzahl der Baumreihen in y-Richtung

for j in range(1,anzahl_y+1):

  for i in range(1,anzahl_x+1):

    baum(a); up(); forward((0.5+random())*5*a); down()

  up(); backward(anzahl_x*5*a); right(90); forward(8*a); left(90); down()

Ausgabe:

12. Beispiel:

Strauch                                  

Programm:

# strauch.py

# Strauch

from turtle import * 

def strauch(a, n):

# Die Prozedur strauch ruft sich rekursiv selber auf!

  if n>0:

     forward(a);left(30); forward(a);

     strauch(a/2,n-1); backward(a); right(30); forward(a);

     right(30); forward(a/2); 

     strauch(a/2,n-1); backward(a/2); left(30); forward(a);

     strauch(a/2,n-1); backward(3*a)

speed(0)

a=30                # Länge a

color("darkgreen")

width(2)            # Strichdicke

left(90)

strauch(a,5)        # Aufruf der Prozedur strauch

hideturtle()

Ausgabe:

13. Beispiel:

Orangenbaum

Programm:

# orangenbaum.py
from turtle import *

def baum(s,t):
    if t>1:
       color("brown")
       for i in range(1,3):
           begin_fill()
           forward(s); left(90)
           forward(3*t); left(90)
           end_fill()
       forward(s)
       left(30)
       baum(s*0.6, t-1)
       right(55)
       baum(s*0.65, t-1)
       left(25) 
       backward(s)
    elif t>=0:
       color("darkgreen")
       begin_fill()
       forward(4*s); circle(2*s); backward(4*s)
       end_fill()
       color("red")
       begin_fill()
       forward(3*s); circle(5); backward(3*s)
       end_fill(); 
       forward(s)
       left(50); 
       color("brown")
       baum(s*0.6, t-1) 
       right(85)
       baum(s*0.65, t-1)
       left(35) 
       backward(s)

setup (width=400, height=400, startx=0, starty=0)
# Fenstergröße
title(" Orangenbaum")
# Fenstertitel

speed(0)
left(90)
width(1)
up()
backward(150)
down()
baum(100,6)

hideturtle()

Ausgabe:

14. Beispiel:

Hochhäuser

Programm:

# hochhaeuser.py
from turtle import *
from random import *

def quadrat(seite):
    color(0.9,0.9,0.9) # hellgrau
    begin_fill()
    for i in range(1,5):
        forward(seite); right(90)
    end_fill()

def rechteck(seite):
    color(random(),0.5,random())
    # (r,g,b), 0<=r,g,b<=1
    begin_fill()
    for i in range(1,3):
        forward(seite); right(90)
        forward(seite/2); right(90)
    end_fill()

def haus(hoehe):
    rechteck(hoehe)
    y_abst=hoehe/11.0
    x_abst=hoehe/10.0
    move(x_abst,y_abst)
    for i in range(1,6):
        quadrat(y_abst)
        move(0,2*y_abst)
    move(2*x_abst,-10*y_abst)
    for i in range(1,6):
        quadrat(y_abst)
        move(0,2*y_abst)
    move(-3*x_abst,-11*y_abst) 

def move(x_abst,y_abst):
    up(); 
    right(90); forward(x_abst); 
    left(90); forward(y_abst); 
    down(); 

setup (width=600, height=300, startx=0, starty=0)
# Windows-Fenstergröße
title(" Hochhäuser")
# Windows-Fenstertitel

speed(0)
left(90)
move(-250,-50)
for i in range(1,11):
    hoehe=randrange(60,120)
    haus(hoehe)
    move(hoehe/2,0)

hideturtle()

Ausgabe:

Zurück

Zurück zur Startseite