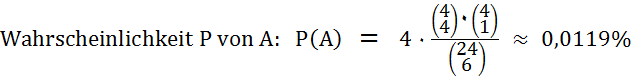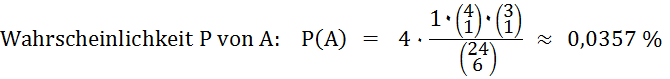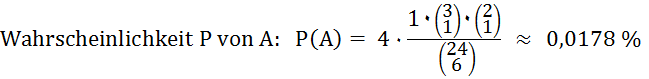|
Berechnung von Wahrscheinlichkeiten und relativen Häufigkeiten bei einem Wenz
1. Fall:
A = „Ein Spieler hat 4 Unter, König und Ober in einer Farbe.“
B
Relative Häufigkeit RH von A:
RH(A)
=
0,0124 %
RH(B) ≈
84
% bei 100 Spielen!
2. Fall:
A = „Ein Spieler hat 4 Unter, König und Ober in 2 verschiedenen Farben.“
B = „Der Ausspieler gewinnt seinen Wenz.“
Bei 20 000 000 Spielsimulationen:
Relative Häufigkeit RH von A:
RH(A) =
0,0349
%
RH(B) ≈
64
% bei 100 Spielen!
3. Fall:
A = „Ein Spieler hat die ersten drei 3 Unter, Herzass, Ober und König in 2
verschiedenen Farben und nicht in
B = „Der Ausspieler gewinnt seinen Wenz.“
1 bedeutet: 3 Unter und Herz-Ass fest
RH(A) =
0,0176 %
RH(B)
≈
61 % bei 100 Spielen!
Python-Programm dazu: RH-Schk-3U-A-K-O
Ausgabe: Kurzer Schafkopf mit 24 Karten; 4 Spieler, 1000000
Spiele 9 = Neuner, 10 = Zehner, U = Unter, O = Ober, K =
König, A = Ass E = Eichel, G = Grün, H = Herz, S = Schellen RH = Relative Häufigkeit
Spieler 1 :
K_S U_H O_E A_H U_E U_G Spieler 2 :
9_S U_S 9_E 9_G K_G O_G Spieler 3 :
10S K_H K_E A_E 9_H O_H Spieler 4 :
10H A_S 10E 10G O_S A_G Spieler 1 :
K_G U_H U_G A_H U_E O_E Spieler 2 :
O_G 9_S 9_E 9_G 10E A_G Spieler 3 :
10H 10G U_S 9_H O_S 10S Spieler 4 :
O_H K_E K_H A_S A_E K_S
Spieler 1 hat 44 -mal U(E-G-H) A-O-K E Download
Python-Programm RH-Schk-3U-A-K-O |