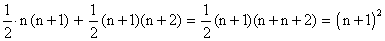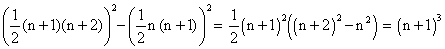|
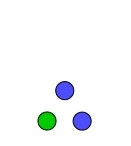
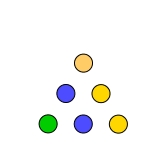
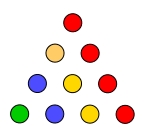
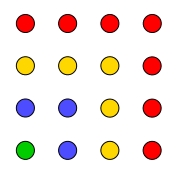
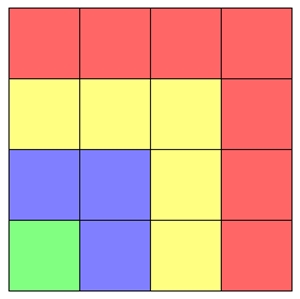
Dreieckszahlen nach Pythagoras
1 3 6 10 (Tetraktys) ... 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, 136, 153,
...
Die Dreieckszahlen entstehen durch Summenbildung der
natürlichen Zahlen: 1 + 2 + 3 + 4 + ... + n,
Die n-te Dreieckszahl ist
Aufgaben und Eigenschaften
1) Bestimme die Summe der
ersten 36 natürlichen Zahlen.
2) 40 Personen treffen sich, wobei jeder jedem die Hand schüttelt.
Wie viele Hände werden geschüttelt?
3) 10 Fußballmannschaften organisieren ein Fußballturnier,
wobei alle Mannschaften gegeneinander spielen sollen.
4) Wie viele Verbindungslinien gibt es zwischen den Punkten eines
15-Ecks?
5) Was ist die Summe zweier aufeinanderfolgender Dreieckszahlen?
6) Was ist die Differenz der Quadrate zweier aufeinanderfolgender
Dreieckszahlen?
7) K. F. Gauß: Eintragung in sein Tagebuch am 10.7.1796: num = Δ + Δ + Δ Jede natürliche Zahl lässt sich als Summe höchstens dreier Dreieckszahlen darstellen. 8)
Die magische Zahl 153 ist die 17. Dreieckszahl, für
die gilt: 9)
Summenformel für Dreieckszahlen
D(a+b) = (a+b)(a+b+1)/2 = a²/2 + a·b + a/2 + b²/2 + b/2 = a(a+1)/2 +
b(b+1)/2 + ab =
Dreieckszahlen als Quasten in den Wappen von kath. Bischöfen und Kardinälen Viereckszahlen (Quadratzahlen) nach Pythagoras
1 4 9 16 ... 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, ... Die „Steinchen", die von einer Viereckszahl auf die nächste dazukommen,
heißen
Gnomon.
Die Viereckszahlen entstehen durch die Summe der
ungeraden Zahlen 1 + 3 + 5 + 7 + ... + (2n
– 1),
Die n-te Viereckszahl ist n2. Beweis und Berechnung Eigenschaften 1) Die Summe der ungeraden Zahlen bis 2n–1 ist die Quadratzahl n2: 1 + 3 + 5 + ... + (2n – 1) = n2 2) Jede Quadratzahl lässt sich als Summe zweier aufeinanderfolgender Dreieckszahlen darstellen, s.o. 5). 3) Das 8-fache einer Dreieckszahl + 1 = Quadratzahl.
4)
Summenformel für Viereckszahlen
V(n) = n²
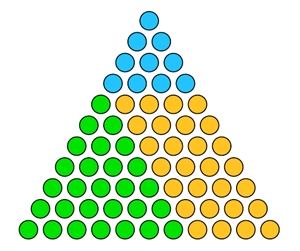
V(a+b) = (a+b)² = a² + 2ab + b² = V(a) + V(b) + 2ab =
= V(a) + V(b) + 2ab
V(a+b) = V(a) + V(b) + 2ab
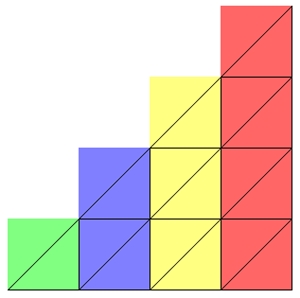
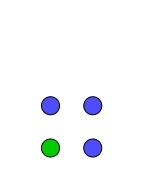
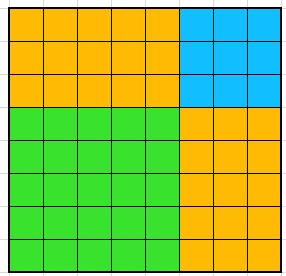
Veranschaulichung für a=5 und b=3:
Fünfeckszahlen (Pentagonalzahlen)
1
5
12
22
…
1, 5, 12, 22, 35, 51, 70, 92, 117, 145, 176, 210,
247, 287, 330, 376, …
Jedes neue Fünfeck entsteht aus dem vorherigen Fünfeck, indem man drei
Seiten des neuen Fünfecks hinzufügt mit 4, 7, 10, … Punkten.
Summenformel für Fünfeckszahlen
F(n) = ½ n (3n – 1) = 1,5 n² – 0,5 n
F(a+b) = ½ (a+b) (3(a+b) – 1) = 1,5 a² + 3ab – 0,5 a + 1,5 b² – 0,5 b =
= F(a) + F(b) + 3ab
F(a+b) = F(a) + F(b) + 3ab
n-Eckszahlen
Diophantos von Alexandria
löste das Problem für beliebige Polygone und den zugeordneten k-Eckszahlen.
Der Wert der n-ten k-Eckszahl Pk(n) beträgt:
Andere Darstellung:
Summenformel für k-Eckszahlen
K(n) = 1/2 n ((n – 1)(k – 2) + 2) =
0.5 k·n² – 0.5 k·n – n² + 2n
K(a+b) = 0.5 k·(a+b)² – 0.5 k·(a+b) –
(a+b)² + 2(a+b) =
= 0,5 ka² – a² + kab – 2ab – 0,5 ka + 2a + 0,5 kb² – b² – 0,5 kb + 2b =
= 0,5 ka² – 0,5 ka – a² + 2a + 0,5 kb² – 0,5 kb – b² + 2·b + kab – 2ab =
= K(a) + K(b) + (k–2) a·b
K(a+b) = K(a) + K(b) + (k–2) ab
Kartenhauszahlen
Ändert man in der Formel für Fünfeckszahlen das Rechenzeichen – zu
+, so erhält man die n-te Kartenhauszahl K(n) = 1/2 n
(3n + 1)
Die n-te Kartenhauszahl K(n) entsteht durch die Summe
2 + 5 + 8 + 11 + … + 3n-1 =
1/2
n (3n + 1)
Folge der Kartenhauszahlen: 2, 7, 15, 26, 40, 57,
77, 100, 126, 155, . . .
2
7
15
26
Legt man beim Kartenhausaufbau die unterste Karte
mit aus, so erhält man folgende Zahlenfolge: 3, 9, 18, 30, 45, 63, 84, 108,
135, 165, . . .
Die n-te Kartenhauszahl K*(n) entsteht durch die Summe
3 + 6 + 9 + 12 + … + 3n = 3 (1 + 2 + 3 + … + n) = 3/2 n (n + 1)
3
9
18
30 . .
.
Die n-te Zahl der Zahlenfolge ist
K*(n) = 3/2 n (n + 1), das dreifache der n-ten Dreieckszahl. Dreiecke in Dreiecksform übereinander liegend
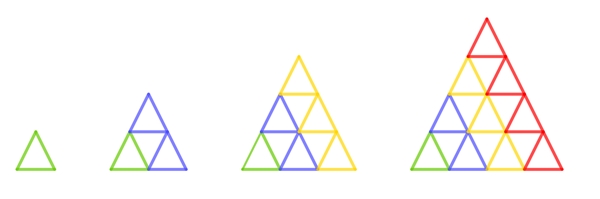
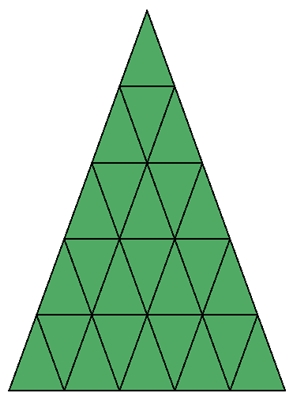
Ein Dreieck aus kongruenten Dreiecken veranschaulicht
die Summe von n ungeraden Zahlen.
Hier ist n = 5.
1 + 3 + 5 + 7 + 9
= 25 = 52
Allgemein gilt:
Die Summe der ersten n ungeraden Zahlen ist n2.
1 + 3 + 5 + … + 2n–1 = n2
(wie bei den Viereckszahlen).
|