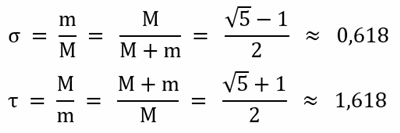Goldener Schnitt in der Natur

Es gelten folgende Bezeichnungen und Beziehungen:

An Stelle von τ (tau) wird auch Φ (Phi) verwendet.

Vorbemerkung zum goldenen Schnitt in der Natur:

Der goldene Schnitt kommt als Verhältnis in vielfältiger Weise in der Natur und auch beim Menschen als Mittelwert vor. Streuungen können dabei sehr groß sein.

Die Quotienten zweier aufeinanderfolgender Fibonacci-Zahlen in der
Fibonacci-Folge 1, 1, 2, 3, 5, 8 ,13, 21, . . .
liefern eine zunehmend bessere Näherung des goldenen Schnitts,
z.B.  3/5 = 0,6,  5/8 = 0,625,  8/13 ≈ 0,615,  13/21 ≈ 0,619
Die Näherung 5/8  = 0,625 stimmt bereits 1% mit dem genauen Wert von σ überein.

Adolf Zeising nahm in seinem Buch über die Proportionen des menschlichen Körpers (1854) an, dass der Nabel die Körpergröße im Verhältnis des goldenen Schnitts teile, und der untere Abschnitt werde durch das Knie wiederum so geteilt. Ferner scheinen die Verhältnisse benachbarter Teile der Gliedmaßen wie beispielsweise bei Ober- und Unterarm sowie bei den Fingerknochen ungefähr in diesem Verhältnis zu stehen.

Beispiele:

Der Mensch

Ausgehend von der Anwendung des goldenen Schnitts auf den menschlichen Körpers, entwickelte 1942 der französische Architekt Le Corbusier seinen Modellmenschen Modulor. Dabei wurde der goldenen Schnitt auf alle möglichen Proportionen der menschlichen Gliedmaßen angewandt.
Nach ihrem Zusammentreffen in Princeton im Jahre 1946 hat Einstein  Le Corbusier über den Modulor geschrieben: "Er ist ein Maßsystem, das das Schlechte schwierig und das Gute leicht macht."

Der Modulor basiert auf den menschlichen Maßen und dem Goldenen Schnitt.

         
Quelle                                                                                                       aus The New York Times for SZ,   Aphrodite von Melos, Louvre, Paris 

Köpfe im goldenen Rechteck:

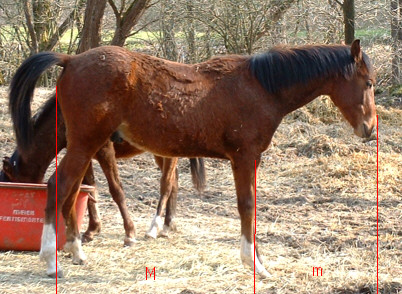
Durchschnittlich steht das Verhältnis Kopfhöhe zu Kopfbreite im goldenen Schnitt  M : m ≈ 1,62.
Auch für Augen, Nase und Mund im Gesicht lassen sich Proportionen im goldenen Schnitt finden.
 

Das Pferd

  
Fotos M. Holzapfel
 

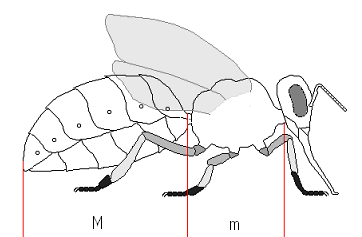
Die Biene

Blumenblüten mit 5-facher Rotationssymmetrie

Diese Blumenblüten haben wie das  regelmäßigen Fünfeck eine 5-fache Rotationssymmetrie und enthalten den goldenen Schnitt (s. Konstruktionen).
 

                Lein                             Enzian                        Dotterblume   

          Hahnenfuß                         Petunie                       Heidenelke

      Storchschnabel                   Weigelie                Wiesenglockenblume

     Glockenblume                  Johanniskraut                 Rosenmalve  

                                           Apfel               Papaya im Querschnitt

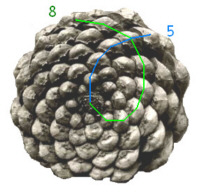
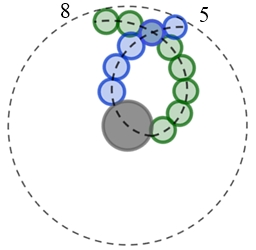
Fotos: M. Holzapfel

Der Pinienzapfen

Linksdrehenden und rechtsdrehenden Spiralbahnen, die das Wachstum kennzeichnen, kann man aufeinanderfolgende Fibonacci-Zahlen zuordnen, deren Verhältnis (hier: 5/8 = 0,625)  in etwa der goldenen Schnittzahl entspricht.

Anordnung von Blättern (Phyllotaxis) bei Pflanzen:

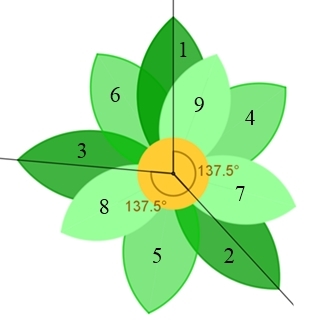
Ein eindrucksvolles Beispiel für den goldenen Schnitt in der Natur findet sich bei der Anordnung von Blättern in den Blütenständen mancher Pflanzen. Ein neues Blatt entsteht dabei im goldenen Winkel zum vorhergehenden Blatt. Die Nummerierung der Blätter stellt die Blattreihenfolge dar.

Durch diese Anordnung der Blätter erhält jedes Blatt einen optimalen Anteil an der Sonneneinstrahlung.

Goldener Winkel = 137,5°  

360° - 360° : τ  = 360° -  360° : 1,618  = 360° - 222,5° ≈ 137,5°

Es gilt:  222,5° : 137,5° = τ  oder 137,5° : 222,5° = σ

Beispiele:

Anordnung von Rosenblättern, Blätter von Kohl

Stilisierte Rose                                 Rosen

Quellen und Links:

http://www.torkado.de/pflanzen.htm

http://www.3d-meier.de/tut22/Sonne/Seite1.html

https://www.biologie-seite.de/Biologie/Goldener_Schnitt

https://www.principia-magazin.de/muster/92-sind-pflanzen-aestheten-oder-mathematiker/