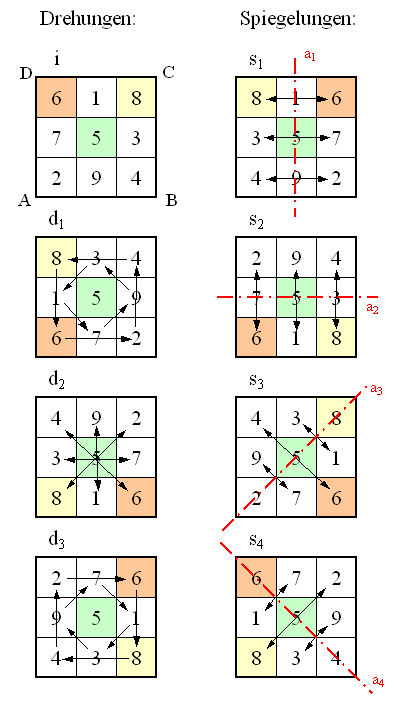
Magisches Quadrat der Ordnung 3 und die DiedergruppeEin natürliches magisches Quadrat der Ordnung 3 besitzt nur eine Grundform und 7 weitere Darstellungsformen, die durch Spiegelungen und Drehungen aus der Grundform hervorgehen. Seine Zeilen-, Spalten- bzw. Diagonal-Summe beträgt 15. Bezeichnungen: d1 : Drehung um 90° gegen den Uhrzeigersinn mit Drehzentrum M (Quadratmitte) d2 : Drehung um 180° gegen den Uhrzeigersinn mit Drehzentrum M
d3
:
Drehung um 270° gegen den
Uhrzeigersinn mit Drehzentrum M oder i = d4 : identische Abbildung = Drehung um 360° gegen den Uhrzeigersinn mit Drehzentrum M. s1 : Spiegelung an der Achse a1 s2 : Spiegelung an der Achse a2 s3 : Spiegelung an der Achse a3 s4 : Spiegelung an der Achse a4 o : Verknüpfung (Hintereinanderausführung) zweier Abbildungen von links nach rechts
Bei
einem beliebigen natürlichen magischen Quadrat
der Ordnung 3 als Grundfigur werden Drehungen und Spiegelungen als Abbildungen
durchgeführt:
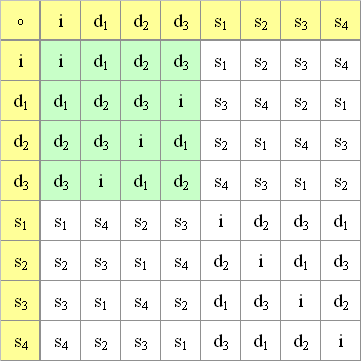
Aus s1, s2 und s3 lassen sich durch Verknüpfungen die anderen Abbildungen herleiten: d3 = s1 o s3, d2 = s1 o s2, d1 = s2 o s3, s4 = s1 o s2 o s3. D4 = { i, d1, d2, d3, s1, s2, s3, s4 } bildet die Diedergruppe der Ordnung 8 mit folgender Verknüpfungstafel (Gruppentafel), wobei die 1. Abbildung in der linken Spalte und die 2. Abbildung in der 1. Zeile steht:
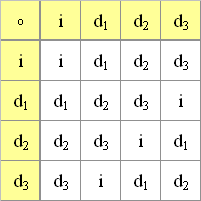
Die Diedergruppe D4 ist nicht kommutativ, da die Gruppentafel nicht symmetrisch zur Hauptdiagonalen ist. Dabei bilden die Drehungen C4 = { i, d1, d2, d3 } eine kommutative zyklische Untergruppe mit folgender Verknüpfungstafel:
d1 ist das erzeugende Element der zyklischen Gruppe: d2 = d1 o d1= d12 d3 = d1 o d1 o d1 = d13 i = d4 = d1 o d1 o d1 o d1 = d14 Damit lässt sich die zyklische Gruppe folgendermaßen angeben: C4 = { i, d1, d12, d13 }
Die Spiegelungen s2, s3, s4 können mit Hilfe der Drehungen d1, d2, d3 und der Spiegelung s1 angegeben werden: s2 = d2 o s1, s3 = d1 o s1, s4 = d3 o s1. Damit lässt sich die Diedergruppe D4 nur mit der Drehung d1 und der Spiegelung s1 erzeugen. D4 = { i, d1, d12, d13, s1, d12 o s1, d1 o s1, d13 o s1 } mit i = d14.
Bemerkung: Ein Quadrat besitzt die gleiche Diedergruppe wie das magische 3 x 3-Quadrat. |