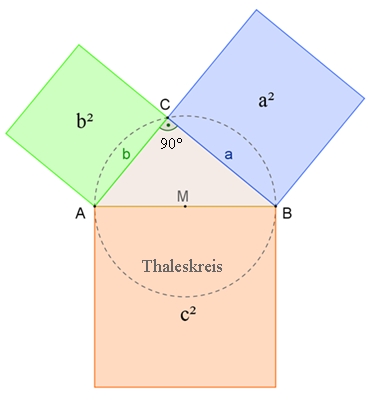
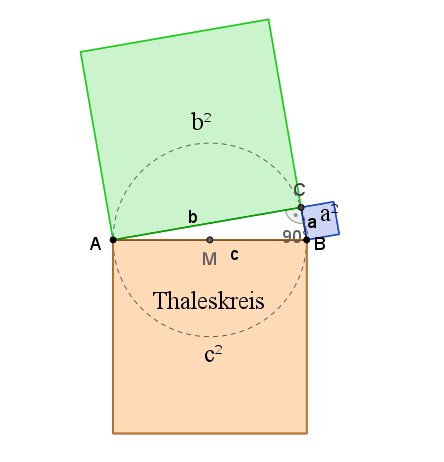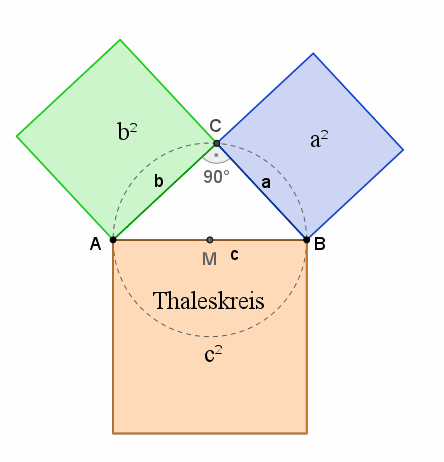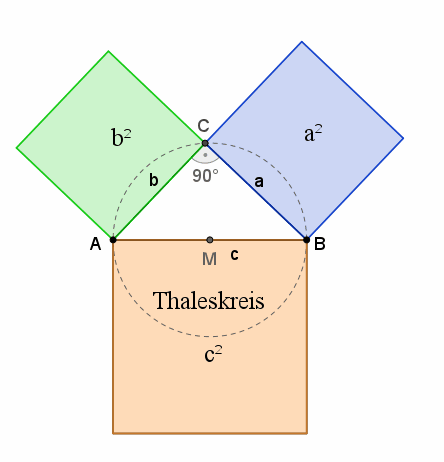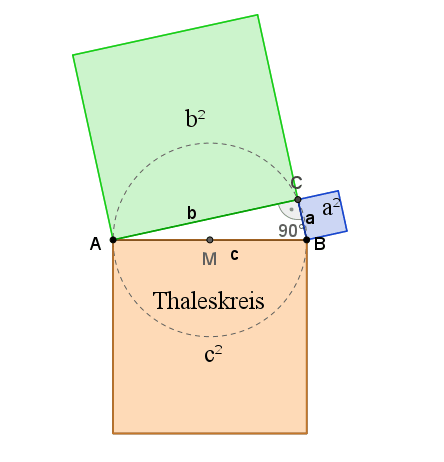
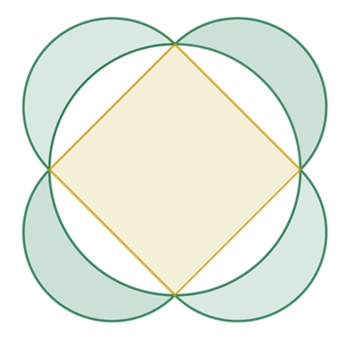
Satz des Pythagoras

Im rechtwinkligem Dreieck ist die Summe der Kathetenquadrate gleich dem Hypotenusenquadrat:

                                                                               a²  +  b²  =  c²

1. Beweis: 

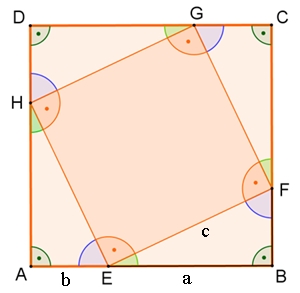
Die vier Dreiecke AEH, BFE, CGF und DHG sind kongruent. Das Viereck EFGH ist ein Quadrat, da die Summe aus grünem und blauem Winkel wegen der Winkelsumme im Dreieck 90° beträgt und der gestreckte Winkel 180° ist. Dann gilt:

Flächeninhalt des großen Quadrats  =  4٠Flächeninhalt eines Dreiecks + Flächeninhalt des inneren Quadrats

                                           (a + b)²  =  4 ٠ ½ ab  +  c²

                              a²  +  2ab  +  b²  =  2ab  +  c²

                                         a²    +  b²  =   c²

2. Beweis:

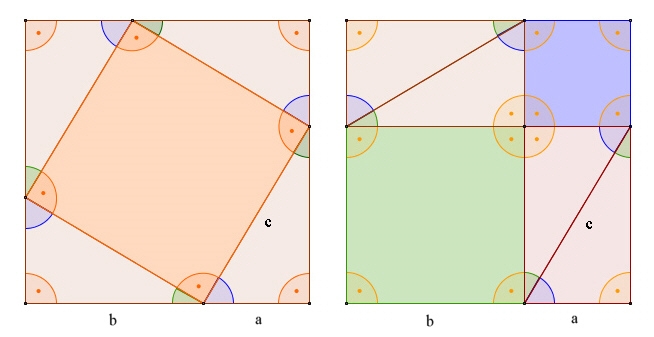
Durch Flächenvergleich der beiden gleich großen Quadrate der Seitenlänge b+a, die jeweils 4 kongruente Dreiecke beinhalten folgt, dass die Restflächen c² (links) und a² + b² (rechts) gleich groß sein müssen.

Konstruktion dynamisch

Die Aussage des Satzes war schon lange vor der Zeit des Pythagoras in Indien bekannt. Der Beweis dieses Satzes wird Babylon und Pythagoras zugeschrieben, obwohl es dafür keinen geschichtlichen Nachweis gibt.

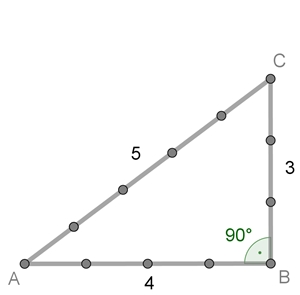
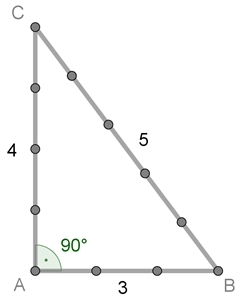
Die Babylonier und Ägypter waren anscheinend nur an der Anwendung des Satzes, nicht an einem allgemeingültigen Beweis interessiert.Die zusammengebundene Zwölfknotenschnur wurde zum Darstellen von rechten Winkeln z.B. im alten Ägypten benutzt. Die Knoten wurden jeweils im gleichen Abstand (L.E.) gebildet. Die Schnur wird so über die Eckpunkte A, B, C aufgespannt, dass die Seitenlängen 3, 4, 5 L.E. betragen. Es gilt dann:  3² + 4²  = 5².
Damit ist ein rechter Winkel im Dreieck ABC gegeben.

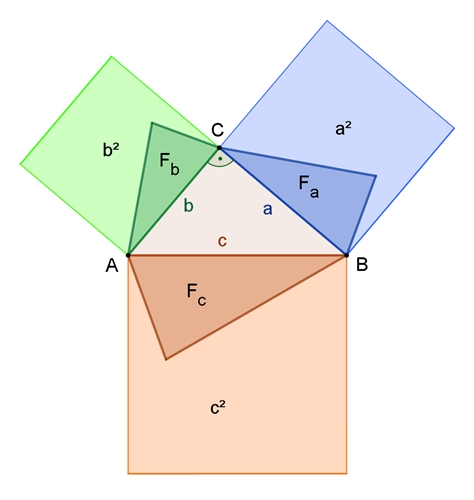
Verallgemeinerung des Satzes von Pythagoras

Errichtet man über den drei Seiten a, b, c des Dreiecks ABC jeweils zueinander ähnliche Figuren mit den Flächeninhalten F_a, F_b, F_c so gilt wegen der Ähnlichkeit:
                                         F_a/a² = F_b/b² = F_c/c²

Daraus folgt:

F_a = F_c /c²٠a²,  F_b = F_c /c²٠b²

F_a + F_b  =  F_c /c²٠a² + F_c /c²٠b²  =  F_c /c²٠(a²+ b²) =  F_c /c²٠c²  = F_c,

da nach Pythagoras gilt:  a² + b² = c²

Pythagoras mit ähnlichen Figuren

Setzt man auf die Seiten a, b. c des rechtwinkligen Dreiecks drei
zueinander ähnliche Figuren mit den Flächeninhalten F_a, F_b , F_c, so gilt:

                               F_a + F_b  =  F_c

(bereits bei Euklid im Buch Elemente. VI.31.[11] ca. 300 v. Chr.)

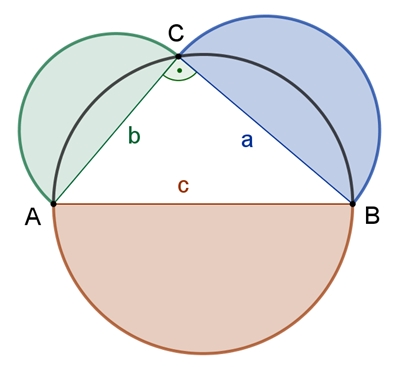
Möndchen des Hippokrates

Nach dem allgemeinen Satz des Pythagoras ist die Summe der Flächeninhalte der Halbkreise über den Seiten a und b gleich dem Flächeninhalt des Halbkreises über der Seite c.

Wenn man den Halbkreis unter AB nach oben klappt und die beiden Kreissegmente aus den beiden kleineren Halbkreisen herausnimmt bleibt die Fläche des Dreiecks ABC übrig. Daraus folgt:

Satz des Hippokrates (um 450 v. Chr.)

Die Summe der Flächeninhalte der beiden Möndchen (Mondsicheln) ist gleich dem Flächeninhalt des Dreiecks ABC.

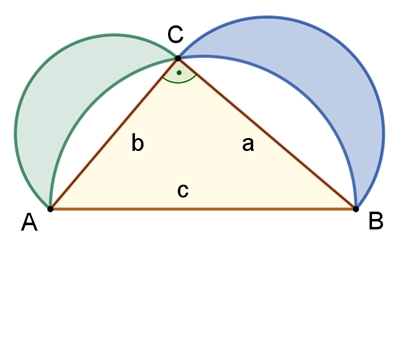
Sonderfall:  gleichschenklig rechtwinkliges Dreieck zum Quadrat verdoppelt

Die Summe der Flächeninhalte der 4 Mondsicheln ist gleich dem Flächeninhalt des Quadrats.

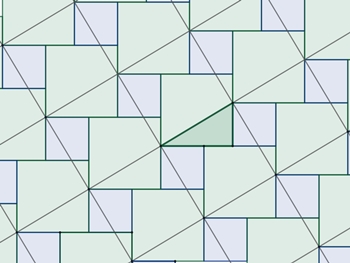
Fliesenbelag mit Bezug zum Pythagoras

In einer derartigen Parkettierung der Ebene durch hellgrüne und hellblaue Fliesen lässt sich der Satz des Pythagoras erkennen. Überzieht man die Quadratfliesen – wie eingezeichnet – mit einem schiefen Quadratgitter, so stellen die schiefen Quadrate Hypotenusenquadrate eines grünen rechtwinkligen Dreiecks dar, während die hellgrünen und hellblauen Quadrate Kathetenquadrate sind.

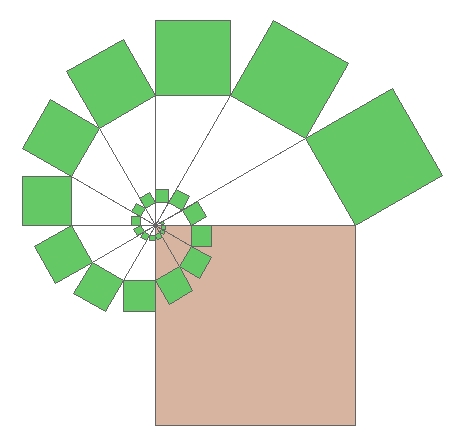
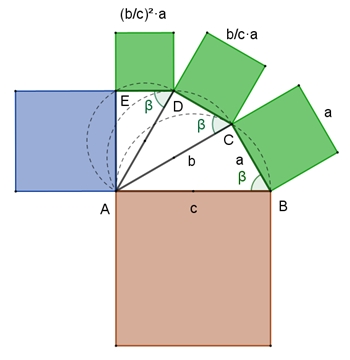
Die Pythagoras-Spirale

Die rechtwinkligen Dreiecke sind zueinander ähnlich.

Dann ist die Summe der Flächeninhalte der grünen Quadrate gleich dem Flächeninhalt des braunen Quadrats.

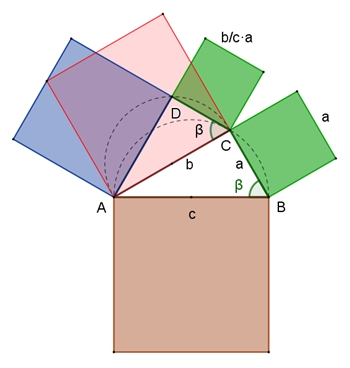
Begründung mit Satz des Pythagoras:

Der Flächeninhalt des roten Quadrats ist gleich der Summe aus den Flächeninhalten des kleinen grünen Quadrats und des blauen Quadrats.

Der Flächeninhalt des braunen Quadrats ist gleich der Summe aus den Flächeninhalten des großen grünen Quadrats und des roten Quadrats.

Daraus folgt:

Der Flächeninhalt des braunen Quadrats ist gleich der Summe aus den Flächeninhalten der grünen Quadrate und des blauen Quadrats.

Entsprechend folgt:

Der Flächeninhalt des braunen Quadrats ist gleich der Summe aus den Flächeninhalten der grünen Quadrate und des blauen Quadrats.

Wenn nun die Anzahl n der so entstandenen grünen Quadrate immer größer wird, nimmt der Flächeninhalt des blauen Quadrats ab und geht gegen 0, wenn n gegen ∞ geht.

Begründung mit der geometrischen Reihe:
1 + q + q² + q³ + … = 1/(1–q)  für |q|<1

Für q = (b/c)² < 1 gilt dann:

a² + (b/c)²٠a² + (b/c)⁴٠a² + (b/c)⁶٠ a²  + … = a²/(1 – (b/c)²)  = a²c²/(c² – b²) = c²

Die grünen Quadrate bilden dabei eine Spirale.

Der Pythagoras-Baum als Fraktal

Zurück
Zurück zur Startseite