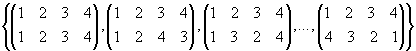Volle Tetraedergruppe Td und symmetrische Gruppe S4
Eigenschaften
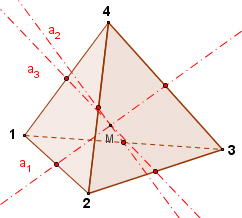
des regulären Tetraeders bezüglich Symmetrie:
-
3
zweizählige Drehachsen a1, a2, a3 durch die Mittelpunkte gegenüberliegender Kanten,
-
4
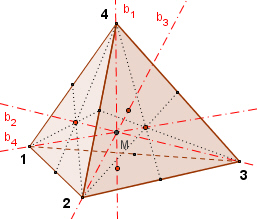
dreizählige Drehachsen b1, b2, b3, b4
durch die Ecken und die Mitten der gegenüberliegenden
Seitenflächen,
-
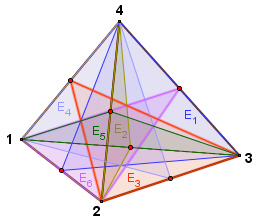
6
Symmetrieebenen E1 bis E6 jeweils durch eine Kante und den
Mittelpunkt der gegenüberliegenden Kante,
-
keine
Punktsymmetrie.
Damit
besitzt das Tetraeder 3*1
+ 4*2 + 1 ( Identität
1) =
12 verschiedene Abbildungen der
Drehgruppe. Diese 12 Elemente der Drehgruppe kombiniert mit den 6
Ebenenspiegelungen und 6 Drehspiegelungen ergeben 24 Abbildungen, die die
Bedingungen einer
Gruppe
erfüllen und die Tetraedergruppe bilden.
1 Identität (identische
Abbildung i)
= Drehung um 360°
Bezeichnungen
für die Abbildungen:
ak1
= Drehung um Achse ak um 180°, jeweils k = 1, 2, 3 (jeweils
zweizählige Drehung)
ak2
= Drehung um Achse ak um 360° = i (identische Abbildung)
bk1
= Drehung um Achse bk um 120°, jeweils k = 1, 2, 3, 4 (jeweils
dreizählige Drehung)
bk2
= Drehung um Achse bk um 240°,
bk3
= Drehung um Achse bk um 360° = i
e1
= Spiegelung an Ebene E1, Eckpunkte 1
und 2 werden vertauscht,
e2
= Spiegelung an Ebene E2, Eckpunkte 1
und 3 werden vertauscht,
e3
= Spiegelung an Ebene E3, Eckpunkte 1
und 4 werden vertauscht,
e4
= Spiegelung an Ebene E4, Eckpunkte 2
und 3 werden vertauscht,
e5
= Spiegelung an Ebene E5, Eckpunkte 2
und 4 werden vertauscht,
e6
= Spiegelung an Ebene E6, Eckpunkte 3
und 4 werden vertauscht.
d1
= Drehspiegelung e6
o
b11 (Verknüpfung von e6 und b11),
d2
= Drehspiegelung e6
o
b21,
d3
= Drehspiegelung e5
o b12,
d4
= Drehspiegelung e5
o
b31,
d5
= Drehspiegelung e4
o
b22,
d6
= Drehspiegelung e4
o
b32.
Volle Tetraedergruppe
Td = { i, a11, a21 a31, b11, b12, b21, b22, b31,
b32, b41, b42, e1, e2, e3, e4,
e5,
e6, d1, d2,
d3, d4, d5, d6 }
Isomorph zur
vollen Tetraedergruppe
Td
ist die symmetrische Gruppe S4 der Permutationen
(Vertauschungen) z.B. der Elemente der Menge {1, 2, 3, 4}.
Isomorphie (Isomorphismus i.Z.
≅) bedeutet dabei eine umkehrbar eindeutige Abbildung
zwischen den beiden mathematischen Strukturen.
Die symmetrische Gruppe S4 besteht aus 24 Elementen, den
Permutationen z.B. der vierelementigen Menge {1, 2, 3, 4}.
a) S4 in Matrixschreibweise:
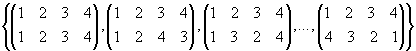
In der 2. Zeile stehen jeweils die zugeordneten Zahlen.
b) S4 in Tupelschreibweise:
{ (1,2,3,4), (1,2,4,3), (1,3,2,4), ..., (4,3,2,1)
}, kurz:
{
1234, 1243, 1324, ..., 4321 }
Sie enthält nur noch die 2. Zeile der Matrixdarstellung.
Die
der vollen Tetraedergruppe Td zugeordnete
symmetrische Gruppe S4 in
entsprechender Reihenfolge:
S4
= { 1234, 2143, 3412, 4321, 2314, 3124, 2431, 4132, 3241, 4213, 1342, 1423,
2134, 3214, 4231, 1324, 1432, 1243, 2341, 2413, 3421, 3142, 4312, 4123 }
Die
Isomorphie entsteht durch die umkehrbar eindeutige Zuordnung der entsprechenden
Elemente:
a11
 2143, a21
2143, a21
 3412, a31
3412, a31
 4321, . . . , d6
4321, . . . , d6
 4123
4123
Gruppentafel
für die Tetraedergruppe Td, entspricht der Gruppentafel für die symmetrische
Gruppe S4:
| o |
i |
a11 |
a21 |
a31 |
b11 |
b12 |
b21 |
b22 |
b31 |
b32 |
b41 |
b42 |
e1 |
e2 |
e3 |
e4 |
e5 |
e6 |
d1 |
d2 |
d3 |
d4 |
d5 |
d6 |
| i |
i |
a11 |
a21 |
a31 |
b11 |
b12 |
b21 |
b22 |
b31 |
b32 |
b41 |
b42 |
e1 |
e2 |
e3 |
e4 |
e5 |
e6 |
d1 |
d2 |
d3 |
d4 |
d5 |
d6 |
| a11 |
a11 |
i |
a31 |
a21 |
b31 |
b41 |
b32 |
b42 |
b11 |
b21 |
b12 |
b22 |
e6 |
d1 |
d2 |
d4 |
d6 |
e1 |
e2 |
e3 |
d5 |
e4 |
d3 |
e5 |
| a21 |
a21 |
a31 |
i |
a11 |
b42 |
b21 |
b12 |
b31 |
b22 |
b41 |
b32 |
b11 |
d3 |
e5 |
d4 |
d2 |
e2 |
d5 |
d6 |
e4 |
e1 |
e3 |
e6 |
d1 |
| a31 |
a31 |
a21 |
a11 |
i |
b22 |
b32 |
b41 |
b11 |
b42 |
b12 |
b21 |
b31 |
d5 |
d6 |
e4 |
e3 |
d1 |
d3 |
e5 |
d4 |
e6 |
d2 |
e1 |
e2 |
| b11 |
b11 |
b42 |
b22 |
b31 |
b12 |
i |
a31 |
b41 |
b21 |
a11 |
a21 |
b32 |
e4 |
e1 |
d1 |
e2 |
d5 |
d2 |
d3 |
d6 |
e3 |
e5 |
d4 |
e6 |
| b12 |
b12 |
b32 |
b41 |
b21 |
i |
b11 |
b31 |
a21 |
a31 |
b42 |
b22 |
a11 |
e2 |
e4 |
d3 |
e1 |
d4 |
d6 |
e3 |
e6 |
d1 |
d5 |
e5 |
d2 |
| b21 |
b21 |
b41 |
b32 |
b12 |
a21 |
b42 |
b22 |
i |
a11 |
b11 |
b31 |
a31 |
e5 |
d2 |
e1 |
d3 |
e3 |
d1 |
d4 |
d5 |
d6 |
e6 |
e2 |
e4 |
| b22 |
b22 |
b31 |
b11 |
b42 |
b32 |
a31 |
i |
b21 |
b41 |
a21 |
a11 |
b12 |
e3 |
d5 |
e5 |
d6 |
e1 |
d4 |
e6 |
e2 |
e4 |
d1 |
d2 |
d3 |
| b31 |
b31 |
b22 |
b42 |
b11 |
b41 |
a11 |
a21 |
b12 |
b32 |
i |
a31 |
b21 |
d4 |
e6 |
e2 |
d1 |
d3 |
e3 |
d5 |
e5 |
d2 |
d6 |
e4 |
e1 |
| b32 |
b32 |
b12 |
b21 |
b41 |
a31 |
b22 |
b42 |
a11 |
i |
b31 |
b11 |
a21 |
d6 |
e3 |
e6 |
d5 |
d2 |
e2 |
e4 |
d3 |
e5 |
e1 |
d1 |
d4 |
| b41 |
b41 |
b21 |
b12 |
b32 |
a11 |
b31 |
b11 |
a31 |
a21 |
b22 |
b42 |
i |
d1 |
d4 |
d5 |
e6 |
e4 |
e5 |
d2 |
e1 |
e2 |
d3 |
d6 |
e3 |
| b42 |
b42 |
b11 |
b31 |
b22 |
b21 |
a21 |
a11 |
b32 |
b12 |
a31 |
i |
b41 |
d2 |
d3 |
d6 |
e5 |
e6 |
e4 |
e1 |
d1 |
d4 |
e2 |
e3 |
d5 |
| e1 |
e1 |
e6 |
d5 |
d3 |
e2 |
e4 |
e3 |
e5 |
d1 |
d2 |
d4 |
d6 |
i |
b11 |
b21 |
b12 |
b22 |
a11 |
b31 |
b32 |
a31 |
b41 |
a21 |
b42 |
| e2 |
e2 |
d6 |
e5 |
d1 |
e4 |
e1 |
d3 |
d4 |
e3 |
e6 |
d5 |
d2 |
b12 |
i |
b31 |
b11 |
a21 |
b32 |
a31 |
b42 |
b21 |
b22 |
b41 |
a11 |
| e3 |
e3 |
d4 |
d2 |
e4 |
d5 |
d6 |
e5 |
e1 |
e6 |
e2 |
d1 |
d3 |
b22 |
b32 |
i |
a31 |
b21 |
b31 |
b41 |
a21 |
b42 |
a11 |
b11 |
b12 |
| e4 |
e4 |
d2 |
d4 |
e3 |
e1 |
e2 |
d1 |
d5 |
d3 |
d6 |
e5 |
e6 |
b11 |
b12 |
a31 |
i |
b41 |
b42 |
b21 |
a11 |
b31 |
a21 |
b22 |
b32 |
| e5 |
e5 |
d1 |
e2 |
d6 |
d2 |
d3 |
e1 |
e3 |
d4 |
d5 |
e6 |
e4 |
b21 |
a21 |
b22 |
b42 |
i |
b41 |
a11 |
b11 |
b12 |
b31 |
b32 |
a31 |
| e6 |
e6 |
e1 |
d3 |
d5 |
d1 |
d4 |
d2 |
d6 |
e2 |
e3 |
e4 |
e5 |
a11 |
b31 |
b32 |
b41 |
b42 |
i |
b11 |
b21 |
a21 |
b12 |
a31 |
b22 |
| d1 |
d1 |
e5 |
d6 |
e2 |
d4 |
e6 |
d5 |
e4 |
d2 |
e1 |
d3 |
e3 |
b41 |
a11 |
b11 |
b31 |
a31 |
b21 |
a21 |
b22 |
b32 |
b42 |
b12 |
i |
| d2 |
d2 |
e4 |
e3 |
d4 |
d3 |
e5 |
d6 |
e6 |
e1 |
d1 |
e2 |
d5 |
b42 |
b21 |
a11 |
a21 |
b32 |
b11 |
b12 |
a31 |
b22 |
i |
b31 |
b41 |
| d3 |
d3 |
d5 |
e6 |
e1 |
e5 |
d2 |
d4 |
e2 |
d6 |
e4 |
e3 |
d1 |
a21 |
b42 |
b12 |
b21 |
b31 |
a31 |
b22 |
b41 |
a11 |
b32 |
i |
b11 |
| d4 |
d4 |
e3 |
e4 |
d2 |
e6 |
d1 |
e2 |
d3 |
d5 |
e5 |
d6 |
e1 |
b31 |
b41 |
a21 |
a11 |
b12 |
b22 |
b32 |
i |
b11 |
a31 |
b42 |
b21 |
| d5 |
d5 |
d3 |
e1 |
e6 |
d6 |
e3 |
e4 |
d1 |
e5 |
d4 |
d2 |
e2 |
a31 |
b22 |
b41 |
b32 |
b11 |
a21 |
b42 |
b12 |
i |
b21 |
a11 |
b31 |
| d6 |
d6 |
e2 |
d1 |
e5 |
e3 |
d5 |
e6 |
d2 |
e4 |
d3 |
e1 |
d4 |
b32 |
a31 |
b42 |
b22 |
a11 |
b12 |
i |
b31 |
b41 |
b11 |
b21 |
a21 |
Beispiel
einer Verknüpfung in Matrixschreibweise:
a11
o
b32
=
b21
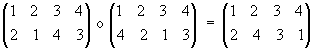
Veranschaulichung:
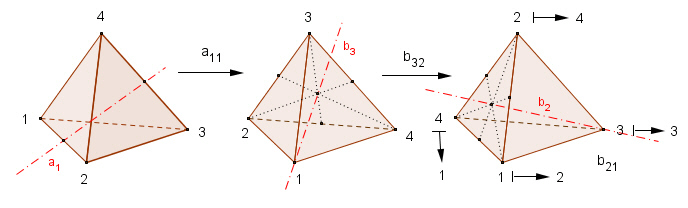
Untergruppen:
Tetraedergruppe T
= { i, a11, a21 a31, b11, b12, b21, b22, b31,
b32, b41, b42 }
≅
Alternierende
Gruppe A4, 12 Elemente (hellblaues Quadrat)
3 Diedergruppen D4:
{ i, a11, a21, a31, e1,
e6,
d3, d5 }, { i, a11, a21 a31, e2,
e5,
d1, d6 }, { i, a11, a21 a31, e3,
e4,
d2, d4 } je 8 Elemente
4
Diedergruppen D3: { i, b11, b12, e1,
e2,
e4 },
{ i, b21, b22, e1,
e3,
e5 }, { i, b31, b32, e2,
e3,
e6 }, { i, b41, b42, e4,
e5,
e6 }
≅
symmetrische
Gruppen S3, je 6 Elemente
Diedergruppe D2
= { i, a11, a21, a31 }
≅
Kleinsche Vierergruppe, 4 Elemente
(dunkelblaues Quadrat)
3 Zyklische
Gruppen C4: { i, a11, e1,
e6 }, {
i, a21, e2,
e5 }, { i, a31, e3,
e4 }, je 4 Elemente
4 Zyklische
Gruppen C3: { i, b11, b12 }, {
i, b21, b22 }, { i, b31,
b32 }, { i, b41,
b42 }, je 3 Elemente
3 Zyklische
Gruppen C2: { i, a11}, { i, a21}, {
i, a31}, je 2 Elemente
Die Diedergruppen D4 in der Gruppentafel:
Diedergruppe D4-1
= { i, a11, a21 a31, e1,
e6, d3, d5 } (hellgrün)
Diedergruppe D4-2
= { i, a11, a21 a31, e2,
e5, d1, d6 } (grün)
Diedergruppe D4-3
= { i, a11, a21 a31, e3,
e4, d2, d4 } (dunkelgrün)
Die Abbildungen i, a11, a21 a31
sind den 3 Gruppen gemeinsam.
|
o |
i |
a11 |
a21 |
a31 |
b11 |
b12 |
b21 |
b22 |
b31 |
b32 |
b41 |
b42 |
e1 |
e2 |
e3 |
e4 |
e5 |
e6 |
d1 |
d2 |
d3 |
d4 |
d5 |
d6 |
|
i |
i |
a11 |
a21 |
a31 |
b11 |
b12 |
b21 |
b22 |
b31 |
b32 |
b41 |
b42 |
e1 |
e2 |
e3 |
e4 |
e5 |
e6 |
d1 |
d2 |
d3 |
d4 |
d5 |
d6 |
|
a11 |
a11 |
i |
a31 |
a21 |
b31 |
b41 |
b32 |
b42 |
b11 |
b21 |
b12 |
b22 |
e6 |
d1 |
d2 |
d4 |
d6 |
e1 |
e2 |
e3 |
d5 |
e4 |
d3 |
e5 |
|
a21 |
a21 |
a31 |
i |
a11 |
b42 |
b21 |
b12 |
b31 |
b22 |
b41 |
b32 |
b12 |
d3 |
e5 |
d4 |
d2 |
e2 |
d5 |
d6 |
e4 |
e1 |
e3 |
e6 |
d1 |
|
a31 |
a31 |
a21 |
a11 |
i |
b22 |
b32 |
b41 |
b11 |
b42 |
b12 |
b21 |
b31 |
d5 |
d6 |
e4 |
e3 |
d1 |
d3 |
e5 |
d4 |
e6 |
d2 |
e1 |
e2 |
|
b11 |
b11 |
b42 |
b22 |
b31 |
b12 |
i |
a31 |
b41 |
b21 |
a11 |
a21 |
b32 |
e4 |
e1 |
d1 |
e2 |
d5 |
d2 |
d3 |
d6 |
e3 |
e5 |
d4 |
e6 |
|
b12 |
b12 |
b32 |
b41 |
b21 |
i |
b11 |
b31 |
a21 |
a31 |
b42 |
b22 |
a11 |
e2 |
e4 |
d3 |
e1 |
d4 |
d6 |
e3 |
e6 |
d1 |
d5 |
e5 |
d2 |
|
b21 |
b21 |
b41 |
b32 |
b12 |
a21 |
b42 |
b22 |
i |
a11 |
b11 |
b31 |
a31 |
e5 |
d2 |
e1 |
d3 |
e3 |
d1 |
d4 |
d5 |
d6 |
e6 |
e2 |
e4 |
|
b22 |
b22 |
b31 |
b11 |
b42 |
b32 |
a31 |
i |
b21 |
b41 |
a21 |
a11 |
b12 |
e3 |
d5 |
e5 |
d6 |
e1 |
d4 |
e6 |
e2 |
e4 |
d1 |
d2 |
d3 |
|
b31 |
b31 |
b22 |
b42 |
b11 |
b41 |
a11 |
a21 |
b12 |
b32 |
i |
a31 |
b21 |
d4 |
e6 |
e2 |
d1 |
d3 |
e3 |
d5 |
e5 |
d2 |
d6 |
e4 |
e1 |
|
b32 |
b32 |
b12 |
b21 |
b41 |
a31 |
b22 |
b42 |
a11 |
i |
b31 |
b11 |
a21 |
d6 |
e3 |
e6 |
d5 |
d2 |
e2 |
e4 |
d3 |
e5 |
e1 |
d1 |
d4 |
|
b41 |
b41 |
b21 |
b12 |
b32 |
a11 |
b31 |
b11 |
a31 |
a21 |
b22 |
b42 |
i |
d1 |
d4 |
d5 |
e6 |
e4 |
e5 |
d2 |
e1 |
e2 |
d3 |
d6 |
e3 |
|
b42 |
b42 |
b11 |
b31 |
b22 |
b21 |
a21 |
a11 |
b32 |
b12 |
a31 |
i |
b41 |
d2 |
d3 |
d6 |
e5 |
e6 |
e4 |
e1 |
d1 |
d4 |
e2 |
e3 |
d5 |
|
e1 |
e1 |
e6 |
d5 |
d3 |
e2 |
e4 |
e3 |
e5 |
d1 |
d2 |
d4 |
d6 |
i |
b11 |
b21 |
b12 |
b22 |
a11 |
b31 |
b32 |
a31 |
b41 |
a21 |
b42 |
|
e2 |
e2 |
d6 |
e5 |
d1 |
e4 |
e1 |
d3 |
d4 |
e3 |
e6 |
d5 |
d2 |
b12 |
i |
b31 |
b11 |
a21 |
b32 |
a31 |
b42 |
b21 |
b22 |
b41 |
a11 |
|
e3 |
e3 |
d4 |
d2 |
e4 |
d5 |
d6 |
e5 |
e1 |
e6 |
e2 |
d1 |
d3 |
b22 |
b32 |
i |
a31 |
b21 |
b31 |
b41 |
a21 |
b42 |
a11 |
b11 |
b12 |
|
e4 |
e4 |
d2 |
d4 |
e3 |
e1 |
e2 |
d1 |
d5 |
d3 |
d6 |
e5 |
e6 |
b11 |
b12 |
a31 |
i |
b41 |
b42 |
b21 |
a11 |
b31 |
a21 |
b22 |
b32 |
|
e5 |
e5 |
d1 |
e2 |
d6 |
d2 |
d3 |
e1 |
e3 |
d4 |
d5 |
e6 |
e4 |
b21 |
a21 |
b22 |
b42 |
i |
b41 |
a11 |
b11 |
b12 |
b31 |
b32 |
a31 |
|
e6 |
e6 |
e1 |
d3 |
d5 |
d1 |
d4 |
d2 |
d6 |
e2 |
e3 |
e4 |
e5 |
a11 |
b31 |
b32 |
b41 |
b42 |
i |
b11 |
b21 |
a21 |
b12 |
a31 |
b22 |
|
d1 |
d1 |
e5 |
d6 |
e2 |
d4 |
e6 |
d5 |
e4 |
d2 |
e1 |
d3 |
e3 |
b41 |
a11 |
b11 |
b31 |
a31 |
b21 |
a21 |
b22 |
b32 |
b42 |
b12 |
i |
|
d2 |
d2 |
e4 |
e3 |
d4 |
d3 |
e5 |
d6 |
e6 |
e1 |
d1 |
e2 |
d5 |
b42 |
b21 |
a11 |
a21 |
b32 |
b11 |
b12 |
a31 |
b22 |
i |
b31 |
b41 |
|
d3 |
d3 |
d5 |
e6 |
e1 |
e5 |
d2 |
d4 |
e2 |
d6 |
e4 |
e3 |
d1 |
a21 |
b42 |
b12 |
b21 |
b31 |
a31 |
b22 |
b41 |
a11 |
b32 |
i |
b11 |
|
d4 |
d4 |
e3 |
e4 |
d2 |
e6 |
d1 |
e2 |
d3 |
d5 |
e5 |
d6 |
e1 |
b31 |
b41 |
a21 |
a11 |
b12 |
b22 |
b32 |
i |
b11 |
a31 |
b42 |
b21 |
|
d5 |
d5 |
d3 |
e1 |
e6 |
d6 |
e3 |
e4 |
d1 |
e5 |
d4 |
d2 |
e2 |
a31 |
b22 |
b41 |
b32 |
b11 |
a21 |
b42 |
b12 |
i |
b21 |
a11 |
b31 |
|
d6 |
d6 |
e2 |
d1 |
e5 |
e3 |
d5 |
e6 |
d2 |
e4 |
d3 |
e1 |
d4 |
b32 |
a31 |
b42 |
b22 |
a11 |
b12 |
i |
b31 |
b41 |
b11 |
b21 |
a21 |
Zwei Diedergruppen D3 in der Gruppentafel:
D3-2 = { i, b11, b12, e1,
e2,
e4
} (hell-lila)
D3-3 ={ i, b31, b32, e2,
e3,
e6 }
(lila)
Die Abbildungen i und e3
sind den 2 Gruppen gemeinsam.
|
o |
i |
a11 |
a21 |
a31 |
b11 |
b12 |
b21 |
b22 |
b31 |
b32 |
b41 |
b42 |
e1 |
e2 |
e3 |
e4 |
e5 |
e6 |
d1 |
d2 |
d3 |
d4 |
d5 |
d6 |
|
i |
i |
a11 |
a21 |
a31 |
b11 |
b12 |
b21 |
b22 |
b31 |
b32 |
b41 |
b42 |
e1 |
e2 |
e3 |
e4 |
e5 |
e6 |
d1 |
d2 |
d3 |
d4 |
d5 |
d6 |
|
a11 |
a11 |
i |
a31 |
a21 |
b31 |
b41 |
b32 |
b42 |
b11 |
b21 |
b12 |
b22 |
e6 |
d1 |
d2 |
d4 |
d6 |
e1 |
e2 |
e3 |
d5 |
e4 |
d3 |
e5 |
|
a21 |
a21 |
a31 |
i |
a11 |
b42 |
b21 |
b12 |
b31 |
b22 |
b41 |
b32 |
b12 |
d3 |
e5 |
d4 |
d2 |
e2 |
d5 |
d6 |
e4 |
e1 |
e3 |
e6 |
d1 |
|
a31 |
a31 |
a21 |
a11 |
i |
b22 |
b32 |
b41 |
b11 |
b42 |
b12 |
b21 |
b31 |
d5 |
d6 |
e4 |
e3 |
d1 |
d3 |
e5 |
d4 |
e6 |
d2 |
e1 |
e2 |
|
b11 |
b11 |
b42 |
b22 |
b31 |
b12 |
i |
a31 |
b41 |
b21 |
a11 |
a21 |
b32 |
e4 |
e1 |
d1 |
e2 |
d5 |
d2 |
d3 |
d6 |
e3 |
e5 |
d4 |
e6 |
|
b12 |
b12 |
b32 |
b41 |
b21 |
i |
b11 |
b31 |
a21 |
a31 |
b42 |
b22 |
a11 |
e2 |
e4 |
d3 |
e1 |
d4 |
d6 |
e3 |
e6 |
d1 |
d5 |
e5 |
d2 |
|
b21 |
b21 |
b41 |
b32 |
b12 |
a21 |
b42 |
b22 |
i |
a11 |
b11 |
b31 |
a31 |
e5 |
d2 |
e1 |
d3 |
e3 |
d1 |
d4 |
d5 |
d6 |
e6 |
e2 |
e4 |
|
b22 |
b22 |
b31 |
b11 |
b42 |
b32 |
a31 |
i |
b21 |
b41 |
a21 |
a11 |
b12 |
e3 |
d5 |
e5 |
d6 |
e1 |
d4 |
e6 |
e2 |
e4 |
d1 |
d2 |
d3 |
|
b31 |
b31 |
b22 |
b42 |
b11 |
b41 |
a11 |
a21 |
b12 |
b32 |
i |
a31 |
b21 |
d4 |
e6 |
e2 |
d1 |
d3 |
e3 |
d5 |
e5 |
d2 |
d6 |
e4 |
e1 |
|
b32 |
b32 |
b12 |
b21 |
b41 |
a31 |
b22 |
b42 |
a11 |
i |
b31 |
b11 |
a21 |
d6 |
e3 |
e6 |
d5 |
d2 |
e2 |
e4 |
d3 |
e5 |
e1 |
d1 |
d4 |
|
b41 |
b41 |
b21 |
b12 |
b32 |
a11 |
b31 |
b11 |
a31 |
a21 |
b22 |
b42 |
i |
d1 |
d4 |
d5 |
e6 |
e4 |
e5 |
d2 |
e1 |
e2 |
d3 |
d6 |
e3 |
|
b42 |
b42 |
b11 |
b31 |
b22 |
b21 |
a21 |
a11 |
b32 |
b12 |
a31 |
i |
b41 |
d2 |
d3 |
d6 |
e5 |
e6 |
e4 |
e1 |
d1 |
d4 |
e2 |
e3 |
d5 |
|
e1 |
e1 |
e6 |
d5 |
d3 |
e2 |
e4 |
e3 |
e5 |
d1 |
d2 |
d4 |
d6 |
i |
b11 |
b21 |
b12 |
b22 |
a11 |
b31 |
b32 |
a31 |
b41 |
a21 |
b42 |
|
e2 |
e2 |
d6 |
e5 |
d1 |
e4 |
e1 |
d3 |
d4 |
e3 |
e6 |
d5 |
d2 |
b12 |
i |
b31 |
b11 |
a21 |
b32 |
a31 |
b42 |
b21 |
b22 |
b41 |
a11 |
|
e3 |
e3 |
d4 |
d2 |
e4 |
d5 |
d6 |
e5 |
e1 |
e6 |
e2 |
d1 |
d3 |
b22 |
b32 |
i |
a31 |
b21 |
b31 |
b41 |
a21 |
b42 |
a11 |
b11 |
b12 |
|
e4 |
e4 |
d2 |
d4 |
e3 |
e1 |
e2 |
d1 |
d5 |
d3 |
d6 |
e5 |
e6 |
b11 |
b12 |
a31 |
i |
b41 |
b42 |
b21 |
a11 |
b31 |
a21 |
b22 |
b32 |
|
e5 |
e5 |
d1 |
e2 |
d6 |
d2 |
d3 |
e1 |
e3 |
d4 |
d5 |
e6 |
e4 |
b21 |
a21 |
b22 |
b42 |
i |
b41 |
a11 |
b11 |
b12 |
b31 |
b32 |
a31 |
|
e6 |
e6 |
e1 |
d3 |
d5 |
d1 |
d4 |
d2 |
d6 |
e2 |
e3 |
e4 |
e5 |
a11 |
b31 |
b32 |
b41 |
b42 |
i |
b11 |
b21 |
a21 |
b12 |
a31 |
b22 |
|
d1 |
d1 |
e5 |
d6 |
e2 |
d4 |
e6 |
d5 |
e4 |
d2 |
e1 |
d3 |
e3 |
b41 |
a11 |
b11 |
b31 |
a31 |
b21 |
a21 |
b22 |
b32 |
b42 |
b12 |
i |
|
d2 |
d2 |
e4 |
e3 |
d4 |
d3 |
e5 |
d6 |
e6 |
e1 |
d1 |
e2 |
d5 |
b42 |
b21 |
a11 |
a21 |
b32 |
b11 |
b12 |
a31 |
b22 |
i |
b31 |
b41 |
|
d3 |
d3 |
d5 |
e6 |
e1 |
e5 |
d2 |
d4 |
e2 |
d6 |
e4 |
e3 |
d1 |
a21 |
b42 |
b12 |
b21 |
b31 |
a31 |
b22 |
b41 |
a11 |
b32 |
i |
b11 |
|
d4 |
d4 |
e3 |
e4 |
d2 |
e6 |
d1 |
e2 |
d3 |
d5 |
e5 |
d6 |
e1 |
b31 |
b41 |
a21 |
a11 |
b12 |
b22 |
b32 |
i |
b11 |
a31 |
b42 |
b21 |
|
d5 |
d5 |
d3 |
e1 |
e6 |
d6 |
e3 |
e4 |
d1 |
e5 |
d4 |
d2 |
e2 |
a31 |
b22 |
b41 |
b32 |
b11 |
a21 |
b42 |
b12 |
i |
b21 |
a11 |
b31 |
|
d6 |
d6 |
e2 |
d1 |
e5 |
e3 |
d5 |
e6 |
d2 |
e4 |
d3 |
e1 |
d4 |
b32 |
a31 |
b42 |
b22 |
a11 |
b12 |
i |
b31 |
b41 |
b11 |
b21 |
a21 |
Die der vollen Tetraedergruppe Td
zugeordnete Gruppentafel der symmetrischen Gruppe S4
|
|
|
i |
a11 |
a21 |
a31 |
b11 |
b12 |
b21 |
b22 |
b31 |
b32 |
b41 |
b42 |
e1 |
e2 |
e3 |
e4 |
e5 |
e6 |
d1 |
d2 |
d3 |
d4 |
d5 |
d6 |
|
o |
1234 |
2143 |
3412 |
4321 |
2314 |
3124 |
2431 |
4132 |
3241 |
4213 |
1342 |
1423 |
2134 |
3214 |
4231 |
1324 |
1432 |
1243 |
2341 |
2413 |
3421 |
3142 |
4312 |
4123 |
|
i |
1234 |
1234 |
2143 |
3412 |
4321 |
2314 |
3124 |
2431 |
4132 |
3241 |
4213 |
1342 |
1423 |
2134 |
3214 |
4231 |
1324 |
1432 |
1243 |
2341 |
2413 |
3421 |
3142 |
4312 |
4123 |
|
a11 |
2143 |
2143 |
1234 |
4321 |
3412 |
3241 |
1342 |
4213 |
1423 |
2314 |
2431 |
3124 |
4132 |
1243 |
2341 |
2413 |
3142 |
4123 |
2134 |
3214 |
4231 |
4312 |
1324 |
3421 |
1432 |
|
a21 |
3412 |
3412 |
4321 |
1234 |
2143 |
1423 |
2431 |
3124 |
3241 |
4132 |
1342 |
4213 |
2314 |
3421 |
1432 |
3142 |
2413 |
3214 |
4312 |
4123 |
1324 |
2134 |
4231 |
1243 |
2341 |
|
a31 |
4321 |
4321 |
3412 |
2143 |
1234 |
4132 |
4213 |
1342 |
2314 |
1423 |
3124 |
2431 |
3241 |
4312 |
4123 |
1324 |
4231 |
2341 |
3421 |
1432 |
3142 |
1243 |
2413 |
2134 |
3214 |
|
b11 |
2314 |
2314 |
1423 |
4132 |
3241 |
3124 |
1234 |
4321 |
1342 |
2431 |
2143 |
3412 |
4213 |
1324 |
2134 |
2341 |
3214 |
4312 |
2413 |
3421 |
4123 |
4231 |
1432 |
3142 |
1243 |
|
b12 |
3124 |
3124 |
4213 |
1342 |
2431 |
1234 |
2314 |
3241 |
3412 |
4321 |
1423 |
4132 |
2143 |
3214 |
1324 |
3421 |
2134 |
3142 |
4123 |
4231 |
1243 |
2341 |
4312 |
1432 |
2413 |
|
b21 |
2431 |
2431 |
1423 |
4213 |
3124 |
3412 |
1423 |
4132 |
1234 |
2143 |
2314 |
3241 |
4321 |
1432 |
2413 |
2134 |
3421 |
4231 |
2341 |
3142 |
4312 |
4123 |
1243 |
3214 |
1324 |
|
b22 |
4132 |
4132 |
3241 |
2314 |
1423 |
4213 |
4321 |
1234 |
2431 |
1342 |
3412 |
2143 |
3124 |
4231 |
4312 |
1432 |
4123 |
2134 |
3142 |
1243 |
3214 |
1324 |
2341 |
2413 |
3421 |
|
b31 |
3241 |
3241 |
4132 |
1423 |
2314 |
1342 |
2143 |
3412 |
3124 |
4213 |
1234 |
4321 |
2431 |
3142 |
1243 |
3214 |
2341 |
3421 |
4231 |
4312 |
1432 |
2413 |
4123 |
1324 |
2134 |
|
b32 |
4213 |
4213 |
3124 |
2431 |
1342 |
4321 |
4132 |
1423 |
2143 |
1234 |
3241 |
2314 |
3412 |
4123 |
4231 |
1243 |
4312 |
2413 |
3214 |
1324 |
3421 |
1432 |
2134 |
2341 |
3142 |
|
b41 |
1342 |
1342 |
2431 |
3124 |
4213 |
2143 |
3241 |
2314 |
4321 |
3412 |
4132 |
1423 |
1234 |
2341 |
3142 |
4312 |
1243 |
1324 |
1432 |
2413 |
2134 |
3214 |
3421 |
4123 |
4231 |
|
b42 |
1423 |
1423 |
2314 |
3241 |
4132 |
2431 |
3412 |
2143 |
4213 |
3124 |
4321 |
1234 |
1342 |
2413 |
3421 |
4123 |
1432 |
1243 |
1324 |
2134 |
2341 |
3142 |
3214 |
4231 |
4312 |
|
e1 |
2134 |
2134 |
1243 |
4312 |
3421 |
3214 |
1324 |
4231 |
1432 |
2341 |
2413 |
3142 |
4123 |
1234 |
2314 |
2431 |
3124 |
4132 |
2143 |
3241 |
4213 |
4321 |
1342 |
3412 |
1423 |
|
e2 |
3214 |
3214 |
4123 |
1432 |
2341 |
1324 |
2134 |
3421 |
3142 |
4231 |
1243 |
4312 |
2413 |
3124 |
1234 |
3241 |
2314 |
3412 |
4213 |
4321 |
1423 |
2431 |
4132 |
1342 |
2143 |
|
e3 |
4231 |
4231 |
3142 |
2413 |
1324 |
4312 |
4123 |
1432 |
2134 |
1243 |
3214 |
2341 |
3421 |
4132 |
4213 |
1234 |
4321 |
2431 |
3241 |
1342 |
3412 |
1423 |
2143 |
2314 |
3124 |
|
e4 |
1324 |
1324 |
2413 |
3142 |
4231 |
2134 |
3214 |
2341 |
4312 |
3421 |
4123 |
1432 |
1243 |
2314 |
3124 |
4321 |
1234 |
1342 |
1423 |
2431 |
2143 |
3241 |
3412 |
4132 |
4213 |
|
e5 |
1432 |
1432 |
2341 |
3214 |
4123 |
2413 |
3421 |
2134 |
4231 |
3142 |
4312 |
1243 |
1324 |
2431 |
3412 |
4132 |
1423 |
1234 |
1342 |
2143 |
2314 |
3124 |
3241 |
4213 |
4321 |
|
e6 |
1243 |
1243 |
2134 |
3421 |
4312 |
2341 |
3142 |
2413 |
4123 |
3214 |
4231 |
1324 |
1432 |
2143 |
3241 |
4213 |
1342 |
1423 |
1234 |
2314 |
2431 |
3412 |
3124 |
4321 |
4132 |
|
d1 |
2341 |
2341 |
1432 |
4123 |
3214 |
3142 |
1243 |
4312 |
1324 |
2413 |
2134 |
3421 |
4231 |
1342 |
2143 |
2314 |
3241 |
4321 |
2431 |
3412 |
4132 |
4213 |
1423 |
3124 |
1234 |
|
d2 |
2413 |
2413 |
1324 |
4231 |
3142 |
3421 |
1432 |
4123 |
1243 |
2134 |
2341 |
3214 |
4312 |
1423 |
2431 |
2143 |
3412 |
4213 |
2314 |
3124 |
4321 |
4132 |
1234 |
3241 |
1342 |
|
d3 |
3421 |
3421 |
4312 |
1243 |
2134 |
1432 |
2413 |
3142 |
3214 |
4123 |
1324 |
4231 |
2341 |
3412 |
1423 |
3124 |
2431 |
3241 |
4321 |
4132 |
1342 |
2143 |
4213 |
1234 |
2314 |
|
d4 |
3142 |
3142 |
4231 |
1324 |
2413 |
1243 |
2341 |
3214 |
3421 |
4312 |
1432 |
4123 |
2134 |
3241 |
1342 |
3412 |
2143 |
3124 |
4132 |
4213 |
1234 |
2314 |
4321 |
1423 |
2431 |
|
d5 |
4312 |
4312 |
3421 |
2134 |
1243 |
4123 |
4231 |
1324 |
2341 |
1432 |
3142 |
2413 |
3214 |
4321 |
4132 |
1342 |
4213 |
2314 |
3412 |
1423 |
3124 |
1234 |
2431 |
2143 |
3241 |
|
d6 |
4123 |
4123 |
3214 |
2341 |
1432 |
4231 |
4312 |
1243 |
2413 |
1324 |
3421 |
2134 |
3142 |
4213 |
4321 |
1423 |
4132 |
3412 |
3124 |
1234 |
3241 |
1342 |
2314 |
2431 |
3412 |
Bemerkungen:
Die volle Tetraedergruppe Td
(d = dot) ist die Punktgruppe aller Symmetrien eines regulären
Tetraeders. Sie besteht aus Drehungen, Spiegelungen und Drehspiegelungen,
die das Tetraeder auf sich abbilden. Td besitzt 24
Gruppenelemente und hat damit die Gruppenordnung 24. Durch das
Durchnummerieren der Eckpunkte des Tetraeders ist die Isomorphie zur
symmetrische Gruppe S4 besser zu erkennen.
Die Tetraedergruppe T ist gleich der
alternierenden Gruppe A4 (in der Gruppentafel hellblau
gekennzeichnet). Sie besteht aus Drehungen, die das Tetraeder auf sich
abbilden. T besitzt 12 Gruppenelemente und hat damit die
Gruppenordnung 12.
Die symmetrische Gruppe
(Permutationsgruppe) S4 besteht aus allen Permutationen
(Vertauschungen) einer 4-elementigen Menge, z.B. {1, 2, 3, 4}.
Nach dem Satz
von Lagrange ist die Ordnung (Anzahl der Elemente) einer Untergruppe zu
einer Gruppe mit der Ordnung n ein echter Teiler von n.
Zurück
Zurück zur Startseite
|