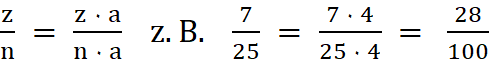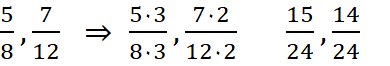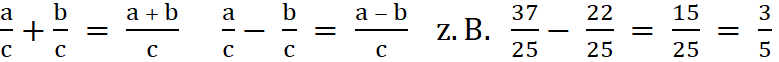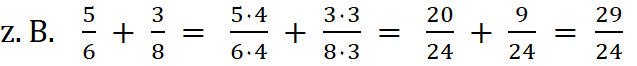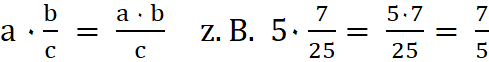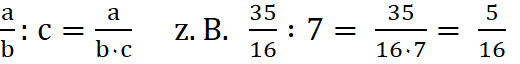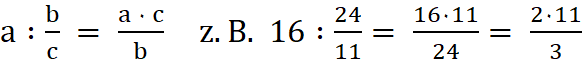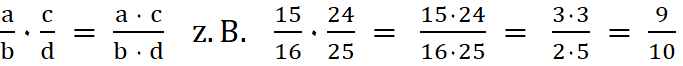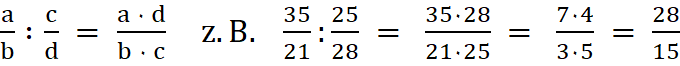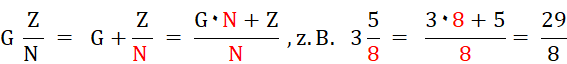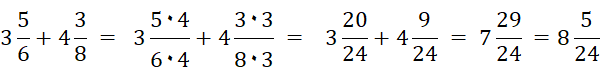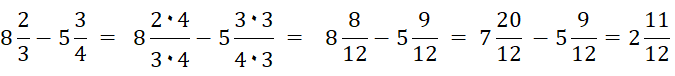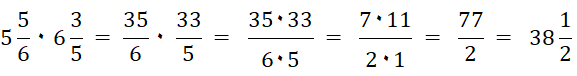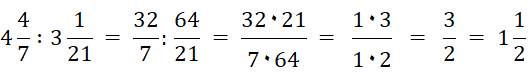Grundrechenarten in der Menge der rationalen Zahlen

Die Menge der rationalen Zahlen wird mit ℚ  bezeichnet.

Sie umfasst die Menge der natürlichen Zahlen ℕ = {1, 2, 3, … }
die Menge der ganzen Zahlen ℤ = { … -3, -2, -1, 0, 1, 2, 3, … }
und die Menge der endlichen oder unendlich periodischen Dezimalzahlen und Brüche.

Dezimalzahlen

Addition und Subtraktion

Bezeichnungen für a + b:   1. Summand + 2. Summand = Wert der Summe

Bezeichnungen für a - b:          Minuend –  Subtrahend = Wert der Differenz

Addiere bzw. subtrahiere die Dezimalzahlen entsprechend ihres Stellenwerts von rechts nach links.

Beispiel für Addition,                                 Subtraktion

  13,46                       28,730                                      
 + 8,375                    - 12,451
  1   1                             1 1         Übertrag

   ──────                                                 ──────   

  21,835                      16,279

Rechen-, Vorzeichen und Klammerregeln siehe Gesetze der Algebra

Multiplikation und Division

Bezeichnungen für a ٠ b:   1. Faktor ٠ 2. Faktor = Wert des Produkts

Bezeichnungen für a : b:        Dividend : Divisor = Wert des Quotienten

Multipliziert man eine Dezimalzahl mit der Stufenzahl 10, 100, 1000, … so rückt das Komma um 1, 2, 3, … Stellen nach rechts.

Dividiert man eine Dezimalzahl durch die Stufenzahl 10, 100, 1000, … so rückt das Komma um 1, 2, 3, … Stellen nach links.

Beispiele:        37,485٠100 = 3748,5;    0,05671٠1000 = 56,71
                        135,78 : 10 = 13,578;     5,87 : 100 = 0,0587

Multiplikation zweier Dezimalzahlen

Multipliziere zunächst ohne Berücksichtigung der Kommas.
Setze das Komma im Ergebnis so, dass es ebenso viele Stellen nach dem Komma hat wie beide Faktoren zusammen.

Beispiel:

5,6٠2,63

─────── 

  112

   336

    168

       1

─────── 

  14,728  3 Stellen = 1 Stelle + 2 Stellen

Potenz als Abkürzung von Produkten mit n (n ϵ ℕ) gleichen Faktoren

a٠a٠a٠…٠a = aⁿ = b,  mit Basis a, Exponent n, Wert der Potenz b
z.B  2⁵ = 32

a) Division einer Dezimalzahl durch eine natürliche Zahl

Division wie bei natürlichen Zahlen. Setze beim Überschreiten des Kommas im Dividenden auch im Ergebnis (Wert des Quotienten) das Komma.

Beispiel:    13,8 = 13,80 Nachnullen dürfen beliebig angefügt werden

 13,80 : 4 = 3,45

-12

  18

 -16

   20

  -20

    0

b) Division eines Dezimalzahl durch eine Dezimalzahl

Verschiebe das Komma bei beiden Zahlen so weit nach rechts, bis der Divisor eine natürliche Zahl ist.

Beispiel:    2,64 = 2,640

  2,64 : 0,015 =    | Komma um 3 Stellen nach rechts verschieben

= 2640 : 15 = 176

 -15

  114

 -105

    90

   -90

     0

c) Periodische Dezimalzahlen

Bei der Division von rationalen Zahlen entstehen entweder endliche Dezimalzahlen oder unendlich periodische Dezimalzahlen.

Beispiele:

1 : 3 = 0,333…  (Periode 3, Periodenlänge 1)

26 : 11 = 2,36 36 36… (Periode 36, Periodenlänge 2)

24 : 7 = 3,428571 428571 428571 … (Periode 428571, Periodenlänge 6)

24 : 70 = 0,3 428571 428571 428571 … (Periode 428571, Periodenlänge 6)

Rechen-, Vorzeichen und Klammerregeln siehe Gesetze der Algebra

Brüche

Der Quotient zweier Zahlen lässt sich auch als Bruch schreiben:

Z : N =  ,  Z = Zähler, N = Nenner

Meist werden für Zähler und Nenner ganze Zahlen verwendet.

Größter gemeinsamer Teiler (ggT)

Gemeinsame Teiler von zwei Zahlen sind die Zahlen, die sowohl Teiler der einen als auch Teiler der anderen Zahl sind. Unter den gemeinsamen Teilern ist die größte Zahl der größte gemeinsame Teiler.

Kleinstes gemeinsames Vielfaches (kgV)

Gemeinsame Vielfache von zwei Zahlen sind die Zahlen, die sowohl Vielfache der einen als auch Vielfache der anderen Zahl sind. Unter den gemeinsamen Vielfachen ist die kleinste Zahl das kleinste gemeinsame Vielfache.

Bruchregeln

1. Einen Bruch kürzen bedeutet Zähler und Nenner durch die gleiche Zahl dividieren. Der Wert des Bruches bleibt gleich.
               15 = ggT(75,30)

2. Einen Bruch erweitern bedeutet Zähler und Nenner mit der gleiche Zahl multiplizieren. Der Wert des Bruches bleibt gleich.
      =  0,28

3. Brüche gleichnamig machen bedeutet die Nenner durch Erweitern oder Kürzen zur gleichen Zahl umzuformen.
                    24 = kgV(8,12)

Bei gleichnamigen Brüchen hat derjenige Bruch den größeren Wert, dessen Zähler den größeren Wert hat.

4a. Bei der Addition und Subtraktion gleichnamiger Brüche werden die Zähler addiert und der Nenner beibehalten.
                  

4b. Bei der Addition und Subtraktion ungleichnamiger Brüche werden die Brüche zuerst gleichnamig gemacht und dann addiert bzw. subtrahiert.

             24 = kgV(6, 8)

5a. Ein Bruch wird mit einer ganzen Zahl multipliziert, indem man den Zähler mit der ganzen Zahl multipliziert und den Nenner beibehält.

                Kürzen mit 5

5b. Ein Bruch wird durch eine ganze Zahl dividiert, indem man den Zähler beibehält und den Nenner mit der ganzen Zahl multipliziert.

              Kürzen mit 7

5c. Eine ganze Zahl wird durch einen Bruch dividiert, indem man die ganze Zahl mit dem Kehrbruch multipliziert.

             Kürzen mit 8

6a.  Zwei Brüche werden multipliziert, indem man die beiden Zähler und die beiden Nenner multipliziert.

            Kürzen mit 5 und 8

6b.  Zwei Brüche werden dividiert, indem man den Kehrbruch des zweiten Bruchs multipliziert.

            Kürzen jeweils mit 7

Brüche werden meist gekürzt!

Gemischte Zahl = ganze Zahl + Bruch

Gemischte Zahl in reinen Bruch umwandeln

Bruch in gemischte Zahl umwandeln

Bei der Addition bzw. Subtraktion gemischter Zahlen werden die Brüche zunächst gleichnamig gemacht und die ganzen Zahlen und die Brüche voneinander getrennt addiert bzw. subtrahiert.

Beispiele:

Bei der Multiplikation bzw. Division gemischter Zahlen werden die gemischten Zahlen in reine Brüche umgewandelt und dann multipliziert bzw. dividiert.

Beispiele:    

Dezimalzahlen in Brüche umwandeln

Beispiele:

Brüche in Dezimalzahlen umwandeln

Beispiele: