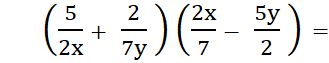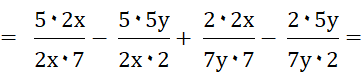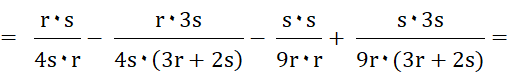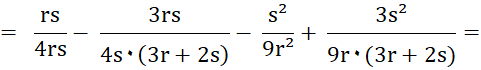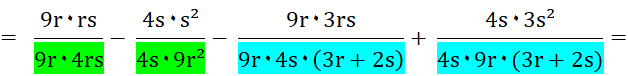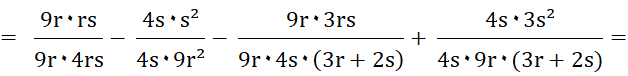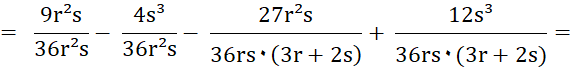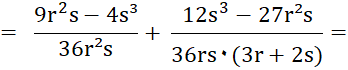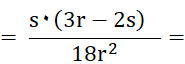Vereinfachen von Termen

Ein Term besteht aus Zahlen, Variablen, Rechenoperationen und Klammern zur Festlegung der Reihenfolge der Berechnung.

Bei der Vereinfachung eines Terms werden die Gesetze der Algebra angewandt.

Zwei Terme, die durch Anwendung der Rechengesetze auseinander  hervorgehen, heißen äquivalent.

Aus den Gesetzen der Algebra folgt, dass Summanden beliebig vertauscht werden dürfen. Da eine Differenz a–b in die Summe a+(–b)  umgewandelt werden kann, dürfen alle Glieder eines Terms einschließlich des Rechenzeichens vertauscht werden.

Es gelten die Vorrangregeln:

Punkt(rechnung ٠  : ) vor Strich(rechnung + –)

Was in Klammern steht wird zuerst berechnet, von inneren Klammern nach außen.

Es wird von links nach rechts gerechnet.

1. Beispiel:

    3٠(1,56 + 2,6) – 2٠(6,7 – 3,38) =  | Der Term stellt eine Differenz dar

=  3٠4,16 – 2٠3,32 =

=  12,48 – 6,64 =  

=  5,84

2. Beispiel:

    2a(9b – 6c) – 3b(2a + 5c) + 6c(2a – b) =   | Der Term ist eine Summe

=  18ab – 12ac – 6ab – 15bc + 12ac – 6bc =  |  ba = ab und ca = ac

=  18ab – 6ab – 12ac + 12ac – 15bc – 6bc =  |  – 12ac + 12ac = 0

=  12ab – 21bc

Bemerkung:  gleichartige Produkte von Variablen können addiert bzw. subtrahiert werden, indem man ihre Zahlenfaktoren addiert bzw. subtrahiert.
Beispiel: 18ab – 6ab = 12ab

3. Beispiel:

    12a + 9b – 2(5a – 3(2a – b)) =  | Der Term ist eine Differenz

=  12a + 9b – 2(5a – 6a + 3b) =

=  12a + 9b – 2(–a + 3b) =

=  12a + 9b + 2a – 6b =

=  12a + 2a + 9b – 6b =

=  10a + 3b

4. Beispiel:

    5a(6 – 4(3 – a)) – (3a(6a – 12) – 12a²) =  | Der Term ist eine Differenz

=  5a(6 – 12 + 4a) – (18a² – 36a – 12a²) =

=  5a(–6 + 4a) – (6a² – 36a) =

=  –30a + 20a² – 6a² + 36a =

=  36a – 30a + 20a² – 6a² =

=  6a + 14a²

Bemerkung:  a und a² sind ungleichartig und können nicht addiert werden!

5. Beispiel:

    (2a – 3b)٠((5a + 7b) – (3a + 4b)) =   |  Der Term ist ein Produkt

=  (2a – 3b) (5a + 7b – 3a – 4b) =

=  (2a – 3b) (2a + 3b) =  (*)    | Binomische Formel III anwenden

=  4a² –  9b²                            |  NR: 2a٠2a = 2٠2٠a٠a = 4a²

(*) = 4a² + 6ab – 6ab – 9b² = |  oder Klammern ausmultiplizieren (auflösen)

=  4a² –  9b²

6. Beispiel:  Bruchterm vereinfachen

    |  Der Term ist ein Produkt

7. Beispiel: Bruchterm vereinfachen (schwierig)

    | Binomische Formel III anwenden

8. Beispiel: Wurzelterm

    7  – 3  – (2  – 3 )² =             |  Binomische Formel II anwenden

=  4  – (4٠3 – 12٠ ٠  + 9٠2) =    | wegen – Zeichen Klammer beibehalten

=  4   – (30 – 12  ) =                         | Klammer auflösen

=  4   – 30 + 12  =

=  16  – 30