Zufallsexperimente und Wahrscheinlichkeit

1.  Zufallsexperimente

Unter einem Zufallsexperiment ZE versteht man einen Versuch, der unter gleichen Bedingungen durchgeführt wird, und bei dem mehrere Ergebnisse zufällig eintreten können.

Beispiele: Werfen einer Münze, Werfen eines Würfels

Die absolute Häufigkeit k gibt an, wie oft ein bestimmtes Ereignis eintritt.

Die relative Häufigkeit h ist der Quotient aus absoluter Häufigkeit k und Anzahl n der Versuche des Zufallsexperiments.

                                                                     h = k : n = k / n  =  

Beispiel: 

Beim 50-maligem Werfen eines Würfels wird 9-mal die Sechs gewürfelt.
Die relative Häufigkeit ist dann h = 9/50 = 0,18

Empirisches Gesetz der großen Zahlen

Wird ein Zufallsexperiment ZE sehr oft ausgeführt, dann stabilisieren sich für jedes Ergebnis die relativen Häufigkeiten um den tatsächlichen Wert der Wahrscheinlichkeit P dieses Ergebnisses.

Beispiel:

Das Zufallsexperiment Münzwurf „Kopf K oder Zahl Z“ lässt sich mit Hilfe eines Computerprogramms simulieren, wobei n sehr große Werte annehmen kann:

n = 1 000 000 Versuche, k(Z) = 499711, h(Z) = 0,499711, P(Z) = 0,5

 
2.  Häufigkeit und Wahrscheinlichkeit

a) Ergebnismenge

Die Menge aller möglichen Ergebnisse eines Zufallsexperiments ZE heißt Ergebnismenge Ω.
Die einzelnen Ergebnisse bezeichnet man mit ω₁, ω₂, ω₃, …

Beispiele:

ZE Werfen eines Würfels:  Ω = {1, 2, 3, 4, 5, 6}

ZE Werfen eines Münze:   Ω = {K, Z}

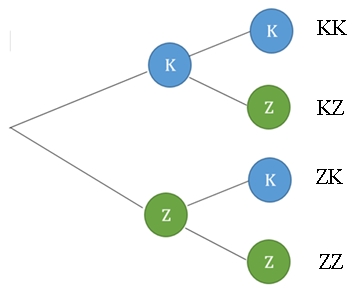
ZE Zweimaliges Werfen einer Münze: Ω = {KK, KZ, ZK ZZ}

Baumdiagramm mit Ergebnissen:

b) Ereignisse

Jede Teilmenge A der Ergebnismenge Ω eines Zufallsexperiments nennt man Ereignis.
Das Ereignis A tritt ein, wenn bei einem Zufallsexperiment ein Ergebnis vorliegt, das in A enthalten ist.

Beispiel:

ZE Werfen eines Würfels,    Ω = {1, 2, 3, 4, 5, 6}

Ereignis A: „Augenzahl ist gerade“,    A = {2, 4, 6}

Ereignis B: „Augenzahl ist ungerade“, B = {1, 3, 5}

Fällt bei einem Wurf die Augenzahl 2, so ist das Ereignis A aber nicht das Ereignis B eingetreten.

c) Relative Häufigkeit und Wahrscheinlichkeit

Tritt bei n-maliger Durchführung desselben Zufallsexperiments ein Ereignis A genau k(A)-mal (absolute Häufigkeit) ein, so heißt der Quotient aus k(A) und n die relative Häufigkeit h(A) des Ereignisses A.

                                              h(A) = k(A) / n

Bei einem  Zufallsexperiment wird jedem Ereignis A eine Wahrscheinlichkeit P(A) zwischen 0 und 1 zugeordnet.
Die Wahrscheinlichkeit P(A) orientiert sich an der relativen Häufigkeit h(A) für sehr große n.

 
3. Laplace-Experimente und Laplace-Wahrscheinlichkeit

Zufallsexperimente, bei denen alle m Ergebnisse gleich wahrscheinlich sind, heißen Laplace-Experimente.
Die Laplace-Wahrscheinlichkeit für jedes einzelne Ergebnis beträgt dann 1/m.

Beispiel: Beim ZE Werfen eines perfekten Würfels ist jede Augenzahl gleichwahrscheinlich,
               die Wahrscheinlichkeit für Augenzahl 6 ist dann 1/6.

 Die Wahrscheinlichkeit P(A) eines Ereignisses A erhält man, indem man die Anzahl |A| der für A günstigen Ergebnisse durch die Gesamtzahl m der möglichen Ergebnisse dividiert.

                                             P(A) = |A| / m,  m = |Ω|

Beispiel:  

ZE Werfen eines Würfels, Ω = {1, 2, 3, 4, 5, 6}
Ereignis A = „Augenzahl ist gerade“ = {2, 4, 6}

Wahrscheinlichkeit von A:                P(A) = 3/6 = 0,5

Es gilt: 

Wahrscheinlichkeit des sicheren Ereignisses Ω:            P(Ω) = 1

Wahrscheinlichkeit des unmöglichen Ereignisses{}:   P({}) = 0

Wahrscheinlichkeit des Gegenereignisses  = Ω \ A zu A:  P( ) = 1 – P(A)

Beispiel:  

ZE Zweimaliges Werfen einer Münze: Ω = {KK, KZ, ZK ZZ}, |Ω| = 4

A = „Mindestens einmal K“,  P(A) = P({KK, KZ, ZK}) =  ¾

 = „Keinmal K“,                 P( ) = P({ZZ}) = ¼ = 1 – ¾

 
4. Zählprinzip und mehrstufige Zufallsexperimente

Zieht man aus k verschiedenen Mengen mit m₁, m₂, m₃, … m_k Elementen jeweils ein Element, so gibt es insgesamt
m₁٠m₂٠m₃٠ …٠m_k Möglichkeiten.

Ein Zufallsexperiment, das aus mehreren Einzelexperimenten zusammengesetzt ist, nennt man mehrstufiges Zufallsexperiment.
Bei n Einzelexperimenten schreibt man die Ergebnisse als n-Tupel (a₁; a₂; a₃; … a_n)  oder kurz  a₁ a₂ a₃…a_n.
Jedes n-Tupel als Ergebnis stellt genau einen Pfad im zugehörigen Baumdiagramm dar.

1. Pfadregel

Bei einem mehrstufigen Zufallsexperiment erhält man die Wahrscheinlichkeit eines Ergebnisses, indem man die Einzelwahrscheinlichkeiten längs des zugehörigen Pfades im Baumdiagramm multipliziert.

Beispiel:  ZE „Hintereinander ziehen einer Kugel aus den Urnen A, B und C mit Zurücklegen und notieren der gezogenen Ziffern“
Urne A mit 2 nummerierten rosa Kugeln, Urne B mit 3 nummerierten türkisen Kugeln, Urne C mit 2 nummerierten gelben Kugeln.

Baumdiagramm:

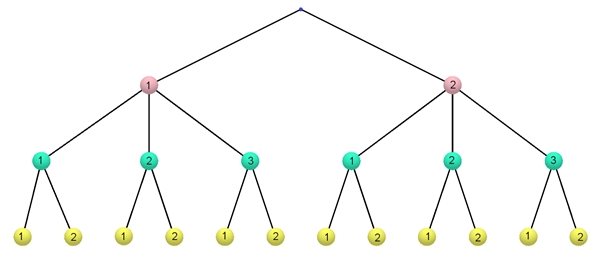Für das Ziehen aus Urne A gibt es 2 Möglichkeiten,
für das Ziehen aus Urne B gibt es 3 Möglichkeiten,
für das Ziehen aus Urne C gibt es 2 Möglichkeiten.
Insgesamt erhält man 2٠3٠2 = 12 mögliche Ergebnisse

Dieses 3-stufige Zufallsexperiment ist ein Laplace-Experiment und die 3-Tupel als Ergebnisse sind gleichwahrscheinlich.
Ω = {111, 112, 121, 122, 131, 132, 211, 212, 221, 222, 231, 232}
A = „3 gleiche Ziffern“ = {111, 222},  P(A) = 2/12 = 1/6

Baumdiagramm:

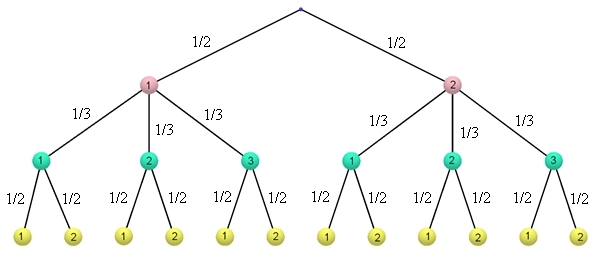Mit der Pfadregel ergibt sich auch für jedes einzelne Ergebnis die Wahrscheinlichkeit 

 
5. Summe von Wahrscheinlichkeiten

2. Pfadregel

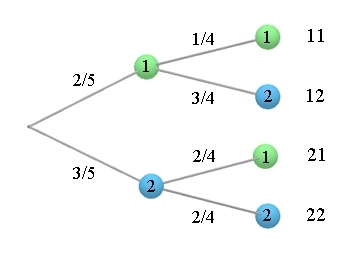
Bei mehrstufigen Zufallsexperimenten erhält man die Wahrscheinlichkeit eines Ereignisses, indem man die Summe der Wahrscheinlichkeiten der Pfade bildet, die zu dem Ereignis gehören.

1. Beispiel:  ZE Aus nebenstehender Urne werden nacheinander zwei Kugeln mit Zurücklegen gezogen.

        Urne:                            Baumdiagramm: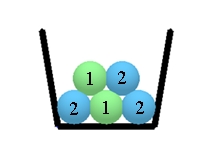

          

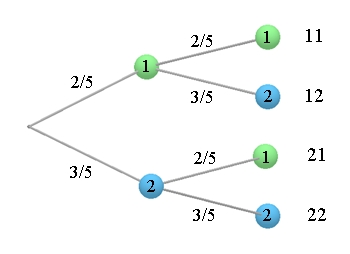Ω = {11, 12, 21, 22}
A = „Zwei gleiche Augenzahlen“ = {11, 22},  P(A) =

2. Beispiel:  ZE Aus der Urne werden nacheinander zwei Kugeln ohne Zurücklegen gezogen.

         Baumdiagramm:

Ω = {11, 12, 21, 22}

A = „Zwei gleiche Augenzahlen“ = {11, 22},  P(A) =

 
6. Vierfeldertafel und bedingte Wahrscheinlichkeit

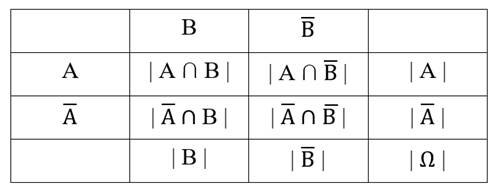
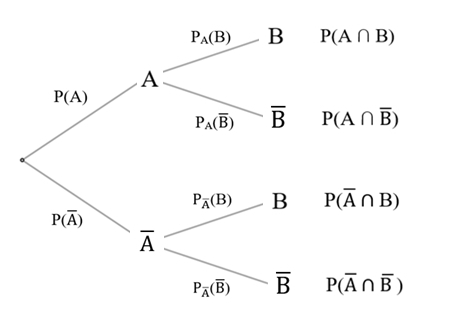
Vierfeldertafel der beiden Ereignisse A und B mit der Anzahl ihrer Elemente (Ergebnisse) |A| und |B|

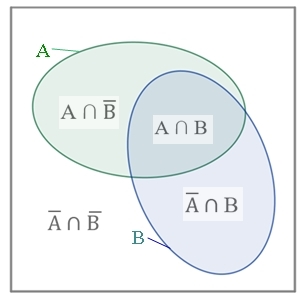
Mengendiagramm von Ω

 

  (lies „A quer“) ist die Komplementärmenge zu A = Ω \ A, lies „Omega ohne A.“

A ∩ B ist die Schnittmenge von A und B, lies „A geschnitten mit B.“

A ∪ B ist die Vereinigungsmenge von A und B, lies: „A vereinigt mit B.“

P(A ∩ B) ist die Wahrscheinlichkeit von A und B.

P(A ∪ B) ist die Wahrscheinlichkeit von A oder B.

 Ω

 

Für die Wahrscheinlichkeit von A oder B gilt:

P(A ∪ B) = P(A) + P(B) – P(A ∩ B)

Begründung:

I         P(A ∪ B) = P(A) + P(  ∩ B)
II        P(B) = P(A ∩ B) + P(  ∩ B)  

1 – II  P(A ∪ B) – P(B) =  P(A) – P(A ∩ B)

           P(A ∪ B) = P(A) + P(B) – P(A ∩ B)

 

Vierfeldertafel der beiden Ereignisse A und B mit der Wahrscheinlichkeit P (oder der relativen Häufigkeit h) von A und B.

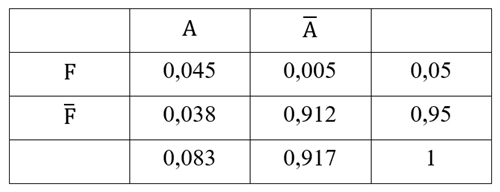
Beispiel:

In einer Firma, die Chips herstellt, sind nach Untersuchungen 5% aller Chips fehlerhaft (F).
90% der fehlerhaften Chips werden bei einem Testverfahren erkannt. Es werden jedoch auch 4% der funktionsfähigen Chips irrtümlich aussortiert.

F = „Chips sind fehlerhaft“,  = „Chips sind in Ordnung“.
A = „Chips werden beim Test aussortiert“,   = „Chips werden beim Test nicht aussortiert“.

Baumdiagramm:

Zugehörige Vierfeldertafel mit Wahrscheinlichkeiten:

Wie groß ist die Wahrscheinlichkeit, dass ein Chip aussortiert wird?
P(A) = P(F ∩ A) + P( A) = 0,045 + 0,038 = 0,083 = 8,3%

Wie groß ist die Wahrscheinlichkeit B, dass ein fehlerhafter Chip nicht aussortiert und ein nicht fehlerhafter Chip aussortiert wird (Sortierfehler)?
P(B) = P(F ∩ ) + P( A) = 0,005 + 0,038 = 0,043 = 4,3%

 
Sind A und B Ereignisse eines Zufallsexperiments mit P(A) ≠ 0, so versteht man unter der bedingten Wahrscheinlichkeit P_A(B) die Wahrscheinlichkeit, dass B unter der Bedingung A eintritt.

Es gilt: P_A(B) =   und  P_B(A) =

Baumdiagramm:

Im obigen Beispiel ist P_F(A) = 90% = 0,9

Wie groß ist im obigen Beispiel P_A(F)?

P_A(F) =    ≈ 0,542 =54,2%

 

---

Zurück
Zurück zu Mathematik-Themen
Zurück zur Startseite