Algebraische Flächen – Körper  

Gegeben sei eine Funktion f(x, y, z) mit (x, y, z) ϵ ℝ³.

Eine algebraische Fläche ist die Menge der Punkte (x, y, z), für die gilt:  f(x, y, z) = 0.

Ebenen

Einfachste algebraische Flächen sind Ebenen.

Die allgemeine Ebenengleichung lautet:  ax + by + cz = d

Beispiel:

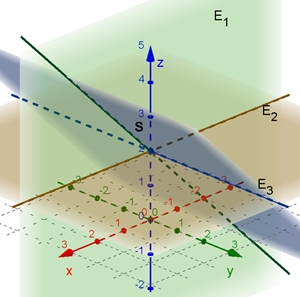
3D-Grafik von E₁, E₂, E₃ mit Schnittgeraden

E₁:  y = 0  (xz-Ebene)

E₂:  z = 2 (Paralle Ebene zur xy-Ebene durch S(0,0,2)

E₃:  z = x + 2

Graphische Darstellung von E1, E2 und E3 mit Variation der Variablen

Klassische Körper

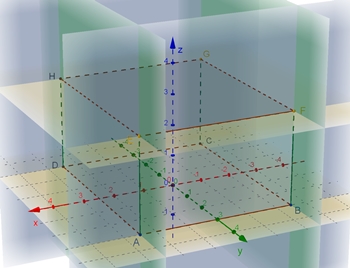
Der Quader wird eingegrenzt durch 6 Ebenen, von denen jeweils 2 parallel sind und sich jeweils 2 Ebenen senkrecht schneiden.

Dadurch werden jeweils 3 parallele gleich große Rechteckflächen eingegrenzt.

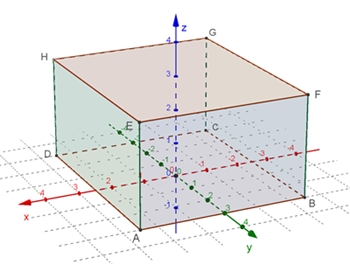
Quader mit der Länge |AB| = a, Breite |BC| = b und Höhe |AE| = c,
dreimal 4 gleich lange Kanten der Länge a, b und c.

Volumen V des Quaders: V = a b c

Oberfläche S des Quaders: S = 2 (a b + a c + b c)

Würfel als Sonderfall des Quaders mit a = b = c,
12 gleich lange Kanten der Länge a.

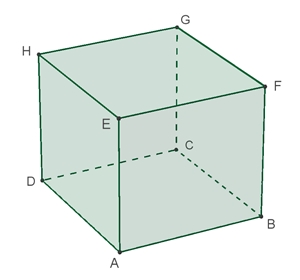
Volumen V des Würfels: V = a³

Oberfläche S des Würfels: S = 6 a²

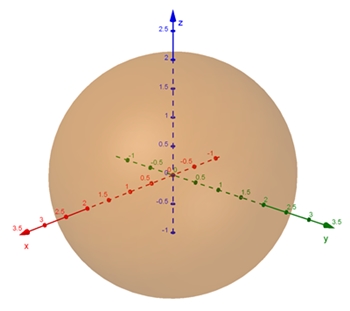
Gleichung der Kugel:

x² + y² + z² = r²

3D-Graph mit r = 2

Volumen V der Kugel: V =  r³ π

Oberfläche S der Kugel: S = 4 r² π

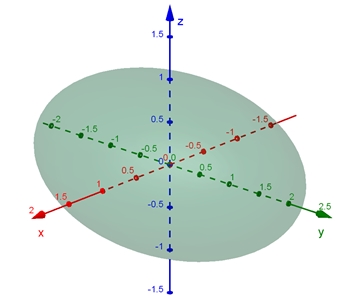
Gleichung des Ellipsoids:

  ,  a, b, c > 0

3D-Graph mit a = 1, b = 2, c = 1

Volumen V des Ellipsoids: V =  a b c π

Kugel als Sonderfall für a = b = c

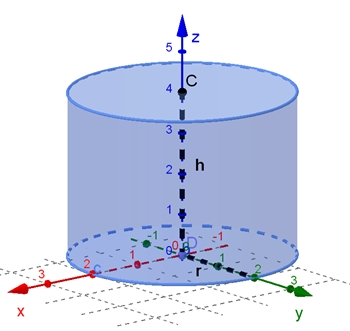
Gleichung des Zylinders:

x² + y² = r²,  0 ≤ z ≤ h

3D-Graph mit r = 2, h = 4

Volumen V des Zylinders: V = r² π h

Grundfläche G des Zylinders: G = r² π

Mantelfläche M des Zylinders: M = 2 r π h

Oberfläche S des Zylinders: S = 2 G + M = r π (r + 2 h)

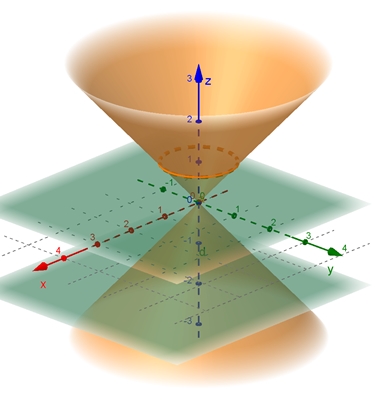
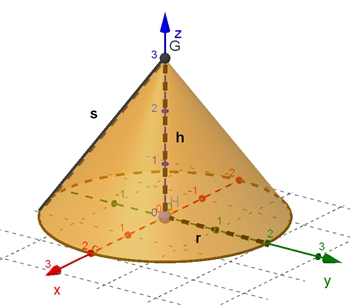
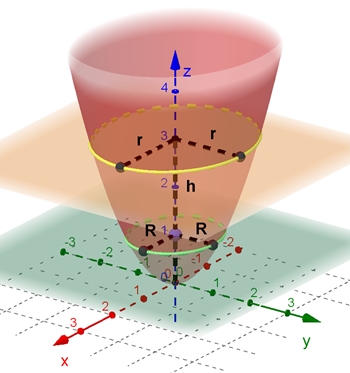
Gleichung des Kegels:

x² + y² = R² z²

R ist Radius des Schnittkreises des Kegelmantels mit der Ebenen z = 1 und z = -1

3D-Graph mit R = 0,8

   Kegel mit Grundfläche G in xy-Ebene und Höhe h:

Volumen V des Kegels: V =   r² π h

Grundfläche G des Kegels: G = r² π

Mantelfläche M des Kegels: M = r s π

Oberfläche S des Kegels: S = r π (r + s)

s = Mantellinie, r = Radius des Kreises in der xy-Ebene

3D-Graph mit r = 2, h = 3

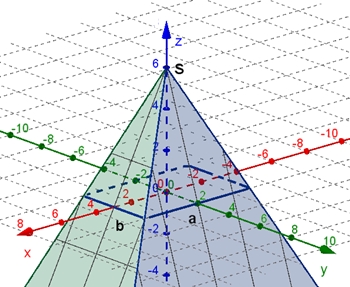
Gleichung einer nach unten offenen geraden Pyramide mit rechteckigem Querschnitt:

z = a – (| x + a y / b | + | x – a y / b |)/c

a und b sind die Seitenlängen des blauen Rechtecks;
das blaue Rechteck ist die Schnittfigur aus dem Pyramidenmantel und der xy-Ebene z = 0.
c > 0 ist ein Maß für den Öffnungswinkel der Pyramide an der Spitze S.

3D-Graph mit a = 3, b = 2 und c = 1,

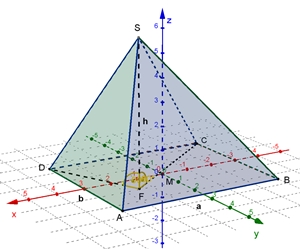
Pyramide mit rechteckiger Grundfläche G = a b und der Höhe h

Volumen V der Pyramide: V =  G h

Oberfläche S der Pyramide: S = G + M

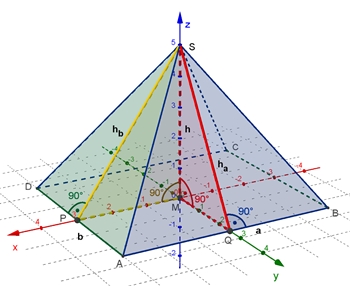
Mantelfläche M = F(ΔABS) + F(ΔBCS) + F(ΔCDS) + F(ΔDAS)

Gerade Pyramide mit rechteckiger Grundfläche G = a b und der Höhe h, die Spitze liegt senkrecht über dem Mittelpunkt M des Rechtecks.

  (Pythagoras im ΔADS)

   (Pythagoras im ΔABS)

Mantelfläche M = 2٠F(ΔADS) + 2٠F(ΔABS)

Mantelfläche

Gleichung des elliptischen  Paraboloids:

,  a, b > 0

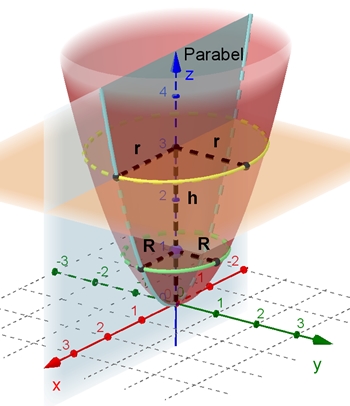
Gleichung des rotationssymmetrischen  Paraboloids: a = b = R

x² + y² = R² z

3D-Graph mit R = 1

Volumen V des Paraboloids mit der Höhe h:
V = ½ r² π h = ½ R π h²  mit  

Parabel als Schnittkurve zwischen Paraboloid und xz-Ebene: 

Mantelfläche M des Paraboloids mit der Höhe h:

Kreisfläche K in Höhe h:  K = r² π = h R π

Oberfläche S = M + K

3D-Graph mit R = 1

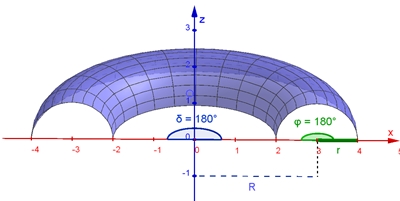
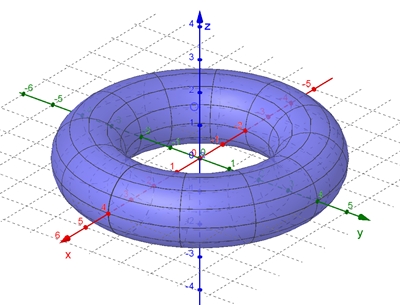
Gleichung des Torus in Parameterform:

x = R + r cos(δ) cos(φ)
y = R + r cos(δ) sin(φ)
z = r sin(δ)

0 ≤ δ ≤ 360°, 0 ≤ φ ≤ 360°

Volumen V des Torus: V = 2 r² R π²  

Oberfläche S des Torus: S = 4 r R π²  

3D-Graph mit R = 3, r = 1

Komplexere Körper

                 3D-Graph                        algebraische Gleichung, Bezeichnung

x³ + y³+ z³ – (x + y + z)² = 0

gleichseitiges Dreiblatt als Ausschnitt

x² + y² + z² + 2xyz - 1 = 0

Caley Cubic, Endraß

von 4 Spitzen im gleichen Abstand ausgehende Kegel

x² + z² - y³ (1,5 - y)³ = 0

Zitrone mit 2 Spitzen

 (x² + y² + z²)² + 8 x y z - 10 (x² +y² + z²) + 25 = 0

Quartic, Tetrahedal

5 Spitzen, 4 halbkugelähnliche Formen

(x²+y²+z²-2)² – 8 (1-z-1,5x)(1-z+1,5x)(1+z+1,5y)(1+z-1,5y) = 0

Quartic Kummer

6 sich öffnende Schalen

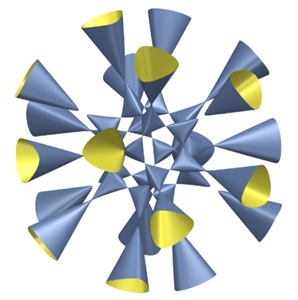
4(q x²-y²)(q y²-z²)(q z²-x²)-(1+2p)(x²+y²+z²-1)² = 0

p = (1 + √5)/2 ≈ 1,62  goldenen Schnittzahl

q = p² ≈ 2,62

Barth Sextic

Quellen:

Algebraische Flächen

Berechnung von Volumen und Oberfläche, siehe Wikipedia:
Kugel, Ellipsoid, Zylinder, Kegel, Paraboloid

Berechnung des Volumens eines Rotationskörpers

Die 3D-Graphen wurden mit den Programmen Geogebra und SURFER erstellt.

Die Bezeichnung Volumen wurde kurz für Volumeninhalt, Oberfläche kurz für Oberflächeninhalt verwendet.

Zurück
Zurück zur Startseite