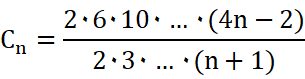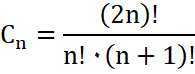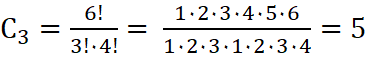Catalan-Zahlen

Die Catalan-Zahlen sind eine Folge natürlicher Zahlen, die in vielen Problemen der Kombinatorik auftreten. Sie wurden nach dem belgischen Mathematiker Eugène Catalan (1814 – 1894) benannt,  der sich intensiv mit diesen Zahlen beschäftigte.
Die Catalan-Zahlen werden mit C₀, C₁, C₂, C₃, … bezeichnet und lauten:

1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, …

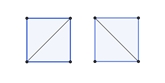
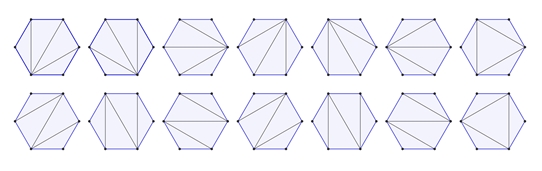
Leonhard Euler (1707 – 1783) fand die Anzahl der Möglichkeiten heraus, ein konvexes n-Eck durch Diagonalen in Dreiecke  zu unterteilen (Triangulation). Diese Anzahl ist C_n-2.
Zum Beispiel gibt es für ein Viereck 2, für ein Fünfeck 5 und für ein Sechseck 14 mögliche Triangulationen:

Euler hat dafür folgende allgemeine Formel für n ≥ 1 aufgestellt:

Allgemein lässt sich C_n für n ≥ 0 auch folgendermaßen darstellen:

z.B.   

TigerJython-Programm zur Berechnung der Catalan-Zahlen

# catalan-zahl

def nfak(n):

  i=1; fak=1

  repeat n:

    fak=fak*i

    i=i+1

  return fak

for i in range(10):

  catalan_zahl = nfak(2*i)/(nfak(i)*nfak(i+1))

  print "%1i," % catalan_zahl,

print "..."

Ausgabe:

1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, …

Weitere Beispiele:

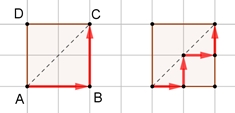
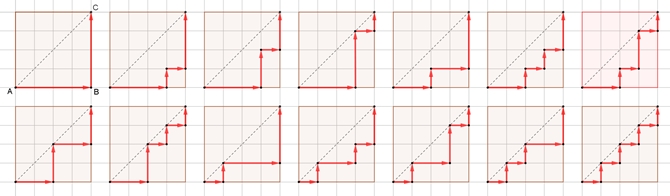
Pfade entlang eines nxn-Gitters, die nicht oberhalb der Diagonale  [AC] verlaufen.

2x2 Gitter: 2 verschiedene Pfade

3x3 Gitter: 5 verschiedene Pfade

4x4 Gitter: 14 verschiedene Pfade

 
Anzahl der Möglichkeiten eine Stufenform der Breite und Höhe n mit n Rechtecken zu kacheln

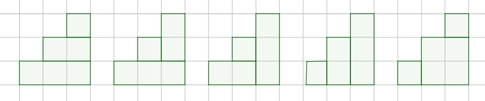
Breite und Höhe 2:  2 mal 2 Rechtecke

Breite und Höhe 3:  5 mal 3 Rechtecke

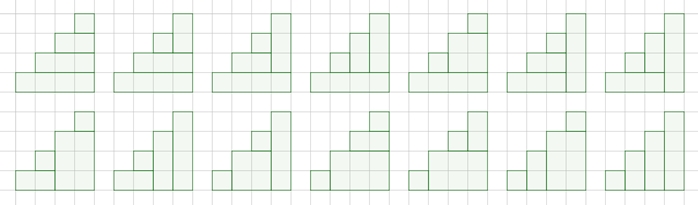
Breite und Höhe 4:  14 mal 4 Rechtecke

Anzahl von Klammerpaaren

2 Klammerpaare: 2 Möglichkeiten

(()), ()()

3 Klammerpaare: 5 Möglichkeiten

((())), (()()), (())(), ()(()), ()()()

4 Klammerpaare: 14 Möglichkeiten

(((()))), (())()(), ()(())(), ()()(()), (())(()), ()((())),((()))(),

(()(())), ((())()), (()())(), ((()())), ()(()()),(()()()), ()()()()