Extremwerte bei Flächen

Rechteck im Dreieck

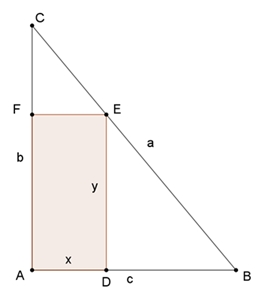
Welches Rechteck, das wie dargestellt von einem rechtwinkligen Dreieck begrenzt wird, hat maximalen Flächeninhalt?

Das rechtwinklige Dreieck ABC ist gegeben durch die Katheten b und c.

y : b = (c – x) : c

y = b (c – x) / c

Flächeninhalt des Rechtecks A = x y

A(x) = b x (c – x) / c
A(x) = b (x – x²/c)
A‘(x) = b (1 – 2x/c)
A‘‘(x) = –2b/c < 0
A‘(x) = 0, daraus folgt: 1 – 2x/c = 0 oder x = c/2

Unabhängig von b wird der Flächeninhalt des einbeschriebenen Rechtecks maximal für x = c/2.

A(c/2) = b/2 ٠ c/2 = b c/4
Folgerung: Der maximale Flächeninhalt ist direkt proportional zur Seitenlänge b.

Rechteck in Parabel

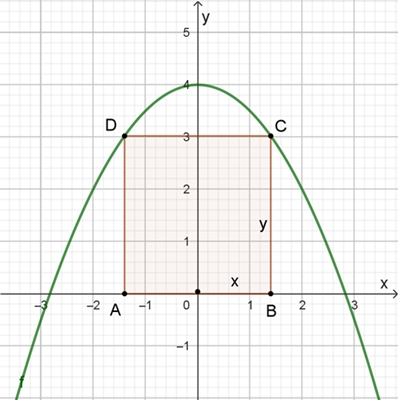
Welches Rechteck, das wie dargestellt von der x-Achse und der Parabel begrenzt wird, hat maximalen Flächeninhalt?

Gegeben ist die Parabel mit der Funktionsgleichung
f(x) = – 0,5 x² + 4   (x in cm)

Flächeninhalt des Rechtecks
A(x) = 2x (– 0,5x² + 4) mit x > 0
A(x) = – x³ + 8x
A‘(x) = – 3x² + 8
A‘‘(x) = – 6 x
A‘(x) = 0 daraus folgt:

– 3x² + 4 = 0 
                x² = 8/3
                 x =  2√6 /3 ≈ 1.63
                 y = 4/3 + 4
                 y = 16/3 ≈ 5,33

A'(2√6 /3) = 0 und A''(2√6 /3) = – 4√6  < 0. Daraus folgt:

Für x =  2√6 /3 beträgt der maximale Flächeninhalt des Rechtecks A = 32√6 /9 ≈ 8,71 (cm²)

Rechtwinkliges Dreieck im Halbkreis

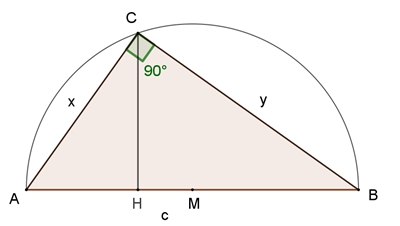
Welches rechtwinklige Dreieck, das wie dargestellt von einem Halbkreis (Thaleskreis) begrenzt wird, hat maximalen Flächeninhalt?

y² + x² = c²  (Pythagoras im Dreieck ABC)

y = √( c² – x²)

Flächeninhalt des Dreiecks ABC: A = xy/2

Flächeninhalt in Abhängigkeit von x:

A(x) = x √( c² – x²) / 2

A‘(x) = ( c² – 2x² ) / (2√( c² – x²))

Aus A‘(x) = 0  folgt:

c² – 2x² = 0 oder x = √2/2 c  ⇨  y = √2/2 c; y = x

A‘‘(x) = x (2x² – 3c²) / (2( c² – x²)^3/2)

A‘(x) = 0  und  A‘‘(√2/2 c) = – 2 c < 0. Daraus folgt:

Der Flächeninhalt ist für x = √2/2 c maximal und beträgt A = c²/4.

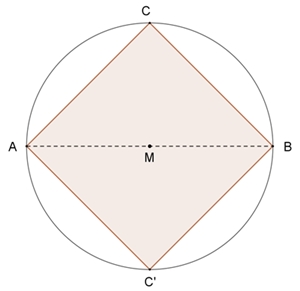
Folgerung:

Unter den einbeschriebenen Rechtecken in einem Kreis besitzt das Quadrat den maximalen Flächeninhalt.

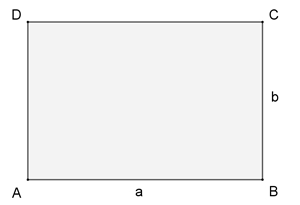
Rechteckfläche mit kürzestem Umfang

x = a und y = b

A = x y  (konstant); y = A/x

Umfang u = 2x + 2y

u(x) = 2x + 2A/x

u‘(x) = 2 – 2A/x² 

u‘‘(x) = 4A/ x³ 

u‘(x) = 0 für 2 – 2A/x² = 0 oder  x² = A
x = √A  und  y = √A

u'(√A) = 0 und u‘‘(√A) = 4/√A > 0. Daraus folgt:

Bei vorgegebener Fläche A hat das Quadrat den geringsten Umfang.

Zurück
Zurück zur Startseite