Funktion

Der Begriff der Funktion

Eine Funktion f ordnet jedem Element x aus der Definitionsmenge D genau ein Element y aus der Wertemenge W zu. Im Zeichen:
f: D → W (Mengenabbildung), f: x ↦ y, x ∊ D (Elementabbildung)
Meist ist die Funktion in Form einer Gleichung y = f(x) gegeben.

Formeln für die Ableitung von Funktionen

f(x) = x^r ⇨ f‘(x) = r x^r-1, r ∊ ℝ (r ist eine reelle Zahl)

f(x) = c ⇨ f‘(x) = 0 (c ist Konstante)

f(x) = c٠g(x) ⇨ f‘(x) = c٠g‘(x)

f(x) = g(x) + h(x) ⇨ f‘(x) = g‘(x) + h‘(x) (Summenregel)

f(x) = g(x) ٠ h(x) ⇨ f‘(x) = g‘(x)٠h(x) + g(x)٠h‘(x) (Produktregel)

f(x) = g(x) / h(x) ⇨ f‘(x) = (g‘(x)٠h(x) – g(x)٠h‘(x)) / (h(x))² (Quotientenregel)

f(x) = g(h(x)) ⇨ f‘(x) = g‘(h(x))٠h‘(x)

Funktion - Veranschaulichung

Anschauliche Bedeutung der 1. und 2. Ableitung einer Funktion

f‘(x_i) > 0, der Graph von f besitzt an der Stelle x_i eine positive Tangentensteigung.

f‘(x_i) < 0, der Graph von f besitzt an der Stelle x_i eine negative Tangentensteigung.

f‘(x_i) = 0 ⇨ An der Stelle x_i gibt es eine Horizontaltangente an den Graphen von f, d.h. an der Stelle x_i gibt es ein relatives Minimum, relatives Maximum oder einen horizontalen Wendepunkt.

f‘‘(x_i) > 0, der Graph von f besitzt an der Stelle x_i eine Linkskrümmung (positiv).
f‘‘(x_i) < 0, der Graph von f besitzt an der Stelle x_i eine Rechtskrümmung (negativ).

f‘(x_i) = 0 und f‘‘(x_i) > 0, der Graph von f besitzt an der Stelle x_i ein relatives Minimum.
f‘(x_i) = 0 und f‘‘(x_i) < 0, der Graph von f besitzt an der Stelle x_i ein relatives Maximum.

f‘‘(x_i) = 0 und f‘‘‘(x_i) ≠ 0, der Graph von f besitzt an der Stelle x_i einen Wendepunkt.

Beim Lösen von Extremwertaufgaben, bei denen Funktionen in Abhängigkeit von x gegeben sind, geht es um die Berechnung und Eigenschaft des Extremwerts (der Extremwerte).

Beispiel 1:

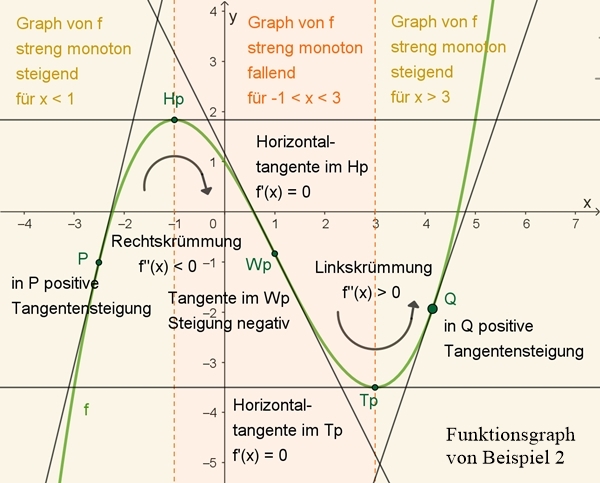
Die Funktion f ist gegeben durch die Gleichung

f(x) = 0,5 x² – 2 x + 1 mit x ∊ ℝ (x ist eine reelle Zahl)

f‘(x) = x – 2 (1. Ableitung)

f‘‘(x) = 1 (2. Ableitung)

Graphische Darstellung der Funktionen f, f‘ und f‘‘

Funktion - 1

Die Ableitung f‘ gibt an jeder Stelle x den Wert der Steigung der Tangente an den Graphen der Funktion f an. Beispiele:
f‘(x) = 0 ⇨ x – 2 = 0; x = 2
f‘(2) = 0
Die Tangentensteigung an der Stelle x₁ = 2 ist gleich 0 und damit gibt es eine Horizontaltangente an den Graphen von f an der Stelle x₁.

x₂ = 4; f‘(4) = 2
Die Tangentensteigung an der Stelle x₂ = 4 ist 2.

x₃ = 0; f‘(0) = –2
Die Tangentensteigung an der Stelle x₃ = 0 ist –2.

f‘(2) = 0 und f‘‘(2) = 1 > 0, daraus folgt:
Die Funktion f hat an der Stelle x₁ = 2 ein relatives Minimum, den Tiefpunkt Tp (2; –1).

Beispiel 2:

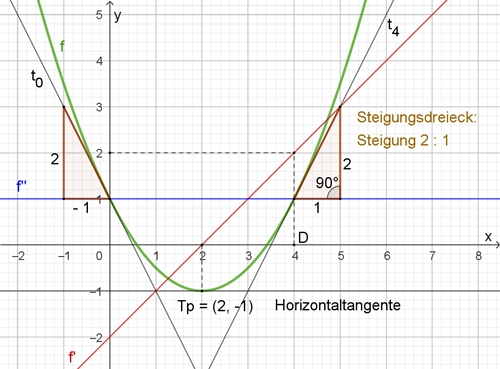
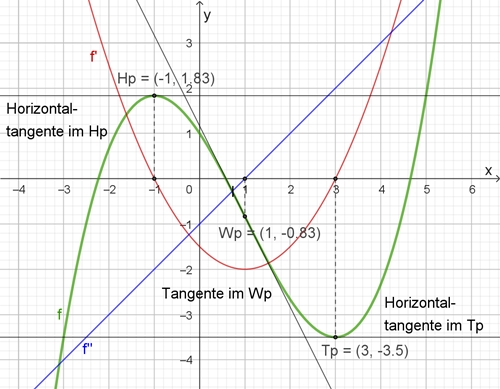
Die Funktion f ist gegeben durch die Gleichung

f(x) = 1/6 x³ – 1/2 x² – 3/2 x + 1 mit x ∊ ℝ

f‘(x) = 1/2 x² – x – 3/2

f‘‘(x) = x – 1

f‘‘‘(x) = –1

Graphische Darstellung der Funktionen f, f‘ und f‘‘

funktion - 2

f‘(x) = 0 ⇨
1/2 x² – x – 3/2 = 0

x₁ = –1; x₂ = 3
f‘(–1) = 0, f‘‘(–1) = –2 < 0 ⇨

Der Graph von f besitzt an der Stelle x₁ ein relatives Maximum, den Hochpunkt Hp (–1; 1,83).
f‘(3) = 0, f‘‘(3) = 2 > 0, daraus folgt:
Der Graph von f besitzt an der Stelle x₂ ein relatives Minimum, den Tiefpunkt Tp (3; 3,5).
f‘‘(x) = 0 ⇨ x₃ = 1
f‘‘(1) = 0, f‘‘‘(1) = –1, daraus folgt:
Der Graph von f besitzt an der Stelle x₃ einen Wendepunkt Wp (1; –0,83).

Beispiel 3:

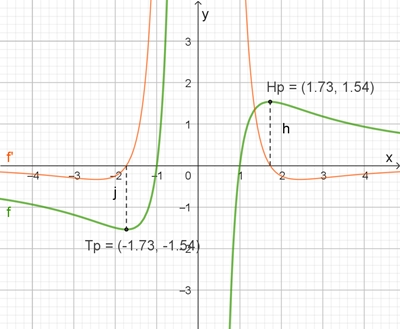
Die Funktion f ist gegeben durch die Gleichung

f(x) = 4 (x² – 1) / x³, x ≠ 0

f‘(x) = 4 (3 – x²) / x⁴

f‘‘(x) = 8 (x² – 6) / x⁵

Graphische Darstellung der Funktionen f, f‘ und f‘‘

Funktion - 3

f‘(x) = 0 ⇨

3 – x² = 0

x₁ = √3; x₂ = – √3

f‘‘(√3) = – 8√3 /9 < 0

f‘(x₁) = 0, f‘‘(x₁) < 0 ⇨

Der Graph von f besitzt an der Stelle x₁ ein relatives Maximum, den Hochpunkt Hp (1,73; 1,54).
f‘(x₂) = 0, f‘‘(x₂) = 8√3 /9 > 0 ⇨

Der Graph von f besitzt an der Stelle x₂ ein relatives Minimum, den Tiefpunkt Tp (–1,73; –1,54).

Beispiel 4:

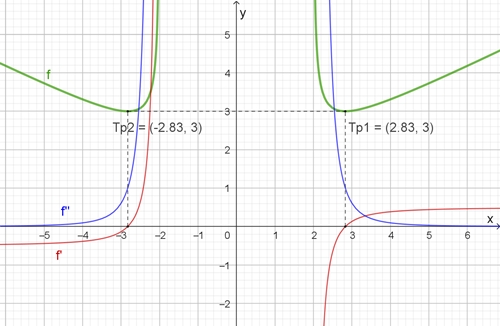
Die Funktion f ist gegeben durch die Gleichung

f(x) = 0.5 x² / √(x² – 4) + 1, |x| > 2

f‘(x) = 0.5 x (x² – 8) / (x² – 4)^3/2

f‘‘(x) = 2 (x² + 8) / (x² – 4)^5/2

Graphische Darstellung der Funktionen f, f‘ und f‘‘

Funktion - 4

f‘(x) = 0 ⇨

x² – 8 = 0

x₁ = 2√2; x₂ = – 2√2 ≈ – 2,83
f‘(x₁) = 0, f‘‘(x₁) = 1 > 0 ⇨
Der Graph von f besitzt an der Stelle x₂ ein relatives Minimum, den Tiefpunkt Tp1 (2,83; 3).
Symmetrisch zur y-Achse liegt der Tp2 (–2,83; 3).

Bemerkung:

Ableitungen von Funktionen lassen sich schnell mit Hilfe von Computer-Algebra-Systemen (CAS) berechnen.

Zurück
Zurück zur Startseite