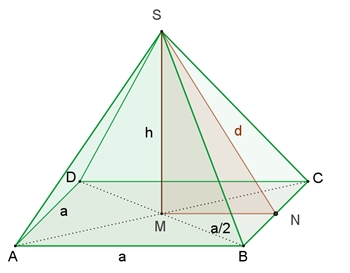
Extremwerte bei Quader und Pyramide

Pyramide mit maximalem Volumeninhalt

a)  Gegeben ist d.

Wie muss a gewählt werden, dass die gerade quadratische Pyramide maximalen Volumeninhalt V annimmt?

Pyramide-1

x = a

d2 = (x/2)2 + h2  (Pythagoras im △MNS)

h = √(d2 – (x/2)2)

V(x) = 1/3 x2 √(d2 – (x/2)2)

V‘(x) = x (8d2 – 3x2) / (6√(4d2 – x2))

Aus V‘(x) = 0 folgt:

8d2– 3x2 = 0  oder  x = 2√6/3 d;  a = x ≈ 1,633 d

V‘‘(x) = (3x4 – 18d2x2 + 16d4) / ((3(4d2 – x2)3/2))

V‘(2√6/3 d) = 0  und V‘‘(2√6/3 d) ≈ - 2,31 d < 0, daraus folgt:


Der Volumeninhalt der Pyramide ist maximal für a ≈ 1,633 d.
 Zum Vergleich: Goldenen Schnittzahl τ ≈ 1,618

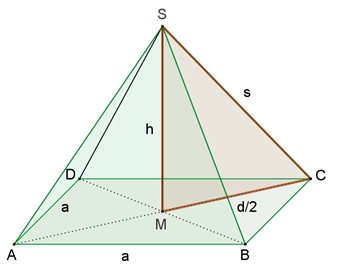
b)  Gegeben ist s.

Wie muss a gewählt werden, dass die gerade quadratische Pyramide maximalen Volumeninhalt annimmt?

Pyramide-2    

h = x

d/2 = a√2/2

x2 + a2/2 = s2 (Pythagoras im △MCS)

a2 = 2(s2 – x2)

V(x) = 2/3 x (s2 – x2)

V‘(x) = 2/3 (s2 – 3 x2)

Für V‘(x) = 0 gilt:  s2 – 3 x2 = 0  oder
x = √3/3 s;  h = x ≈ 0.577 s

Für a = √( 2(s2 – x2))  folgt:
a = 2√3/3 s ≈ 1,155 s

V‘‘(x) = – 4 x

Aus V‘(√3/3 s) = 0 und  V‘‘(√3/3 s) = – 4√3/3 s < 0 folgt:

Der Volumeninhalt der Pyramide ist maximal für a ≈ 1,155 s.

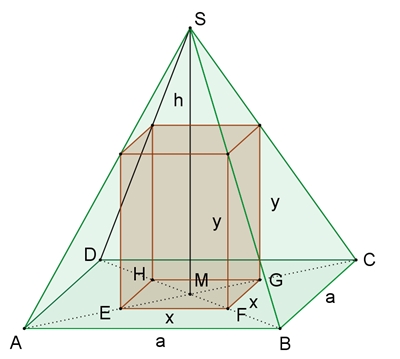
Quader in Pyramide

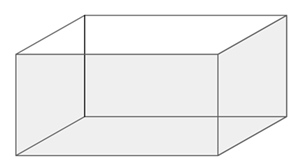
Ein Quader mit quadratischer Grundfläche wird in eine gerade quadratische Pyramide – wie dargestellt – einbeschrieben. Für welche Seitenlängen wird der Volumeninhalt des Quaders maximal?

Quader in Pyramide

|BF| = d, |BM| = e

y : h = d : e  (1)

(e – d) : e = x : a;  1 – d : e = x : a  (2)

(1) in (2):  1 – y : h = x : a 

                  1 – x/a  =  y/h

                  y  =  h (1– x/a)

Volumeninhalt des Quaders

V(x) = x2 h/a (a – x)

V‘(x) = h/a (2ax – 3x2)

Aus V‘(x) = 0 folgt:

2ax – 3x2 = 0 | : x > 0

x = 2/3 a

y = h (1 – 2/3);  y = 1/3 h

V‘‘(x) = h/a (2a – 6x)

V‘‘(2/3 a) = – 2 h < 0

Der Quader besitzt für x = 2/3 a und y = 1/3 h maximalen Volumeninhalt.

 

Karton

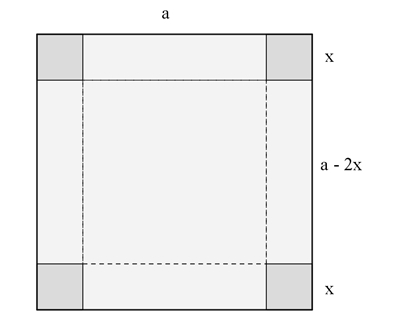
Aus einem quadratischen Karton der Seitenlänge a kann durch Herausschneiden von gleich großen Quadraten der Kantenlänge x an den Ecken und hochklappen der Seiten eine Schachtel hergestellt werden. Wie groß muss x gewählt werden, damit der Volumeninhalt der Schachtel maximal wird?

Karton

 

  

Volumeninhalt der Schachtel in Abhängigkeit von x:

V(x) = (a – 2x) x = ax – 2x2

V‘(x) = a – 4x

V‘(x) = 0 für a – 4x = 0 oder x = a/4

V‘‘(x) = – 4 < 0, daraus folgt:

Für x = a/4 hat die Schachtel maximalen Volumeninhalt.

 

 

Karton-2  
   Beispiel:

   Karton mit a = 20 cm, x = 5 cm

  

  

Optimierte 1-Liter-Milchtüte, 1 Liter = 1000 dm³

Für welche rechteckförmige Tütenvorlage für eine 1-Liter-Milchtüte wird der Flächeninhalt minimal?

Die Tüten werden bis 2 cm unter dem Rand gefüllt. h = Höhe der Tüte; Milchhöhe h – 2.

Milchtuete

 

x2 (h – 2) = 1000

h = 1000/ x2 + 2

Fläche der Milchtüte:

A(x) = (4x + 0,5) (1000/x2 + x + 4)

A(x) = 4x2 + 16,5x + 4000/x + 500/x2 + 2

A‘(x) = 8x – 4000/x2 – 1000/x3 + 16,5

Für A‘(x) = 0 gilt:

8x – 4000/x2 -1000/x3 + 16,5 = 0  oder

(16x4 +33x3 - 8000x – 2000) / (2x3) = 0

Positive Lösung x ≈ 7,39 cm

A‘‘(x) = 8000/x3 + 3000/x4 + 8

A‘‘(7,39) ≈ 28,8 > 0 ,

A‘(x) = 0 und A‘‘(x) > 0, daraus folgt:

Der Flächeninhalt einer rechteckförmigen Tütenvorlage für eine 1-Liter-Milchtüte wird für x ≈ 7,39 cm minimal.  

Milchtuete-2

h = 1000/ 7,392 + 2 ≈ 20,3.

Die Höhe der Milchtüte beträgt dann 20,3 cm.

 

Milchtüte als Quader mit Klebekanten

 

 

 

 

Zurück
Zurück zur Startseite