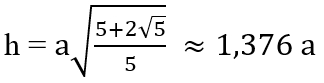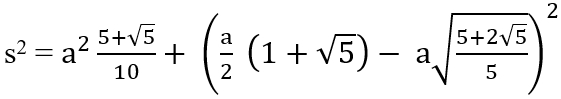Vom Ikosaeder zum Klettergerüst

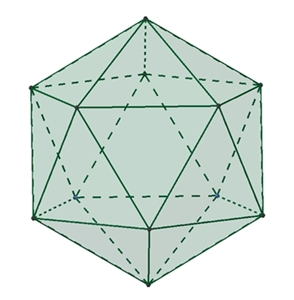
Der Ikosaeder ist ein platonischer Körper, der von 20 deckungsgleichen (kongruenten) gleichseitigen Dreiecken begrenzt wird.

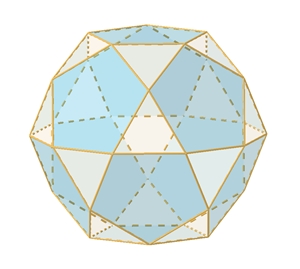
Wenn man die Mittelpunkte der Kanten verbindet, erhält man den Ikosidodekaeder.

Er besteht aus 12 kongruenten regulären Fünfecken und 20 kongruenten gleichseitigen Dreiecken.

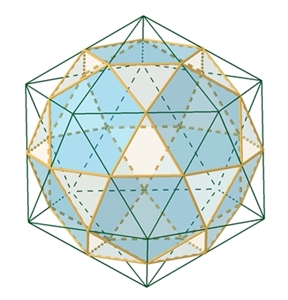
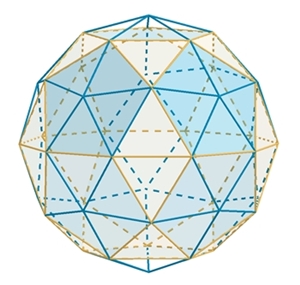
Über den Eckpunkten der regulären Fünfecke werden nun 5 gleich lange Strecken so angeordnet, dass sie sich in einem gemeinsamen Punkt treffen, der auf der Umkugel um den Ikosidodekaeder liegt. Damit entsteht ein erweiterter Ikosidodekaeder.

Für den Umkugelradius R eines erweiterten Ikosidodekaeders mit der Seitenlänge a der gleichseitigen Dreiecke bzw. Fünfecke gilt:

  (goldene Schnittzahl τ ≈ 1,618)

Senkrechter Querschnitt durch den erweiterten Ikosidodekaeder mit einem regulären Fünfeck im Ausschnitt:

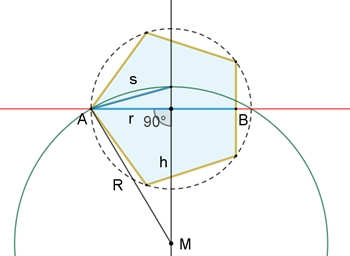
Das reguläre Fünfeck, das in der zur senkrechten Querschnittsebene durch AB gehende Ebene liegt, wird um die Achse AB um 90° zur besseren Darstellung gedreht.

Für den Umkreisradius r des regulären Fünfecks gilt:

h² = R² – r²  (Pythagoras)

s² = r² + (R–h)²  (Pythagoras)

s ≈ 0,884 a

Der erweiterte Ikosidodekaeder kann als gutes Kantenmodell einer Kugel betrachtet werden.

Ein käuflich erwerbbares Klettergerüst hat die obere Hälfte des erweiterten Ikosidodekaeders als Vorlage.  

Die Stangenmaße bis zu den Verschraubungen sind a ≈ 85 cm und s ≈ 75 cm.

Für a = 85  folgt aus der Berechnung s ≈ 75,1.

                            Klettergerüst und Konstruktion mit geogebra zum Vergleich

Zurück
Zurück zur Startseite