Rosenkurven (Rhodoneen)

„Im großen Garten der Geometrie kann sich jeder
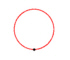
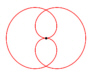
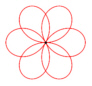
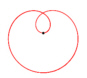
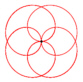
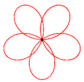
nach seinem Geschmack einen Strauß pflücken.“

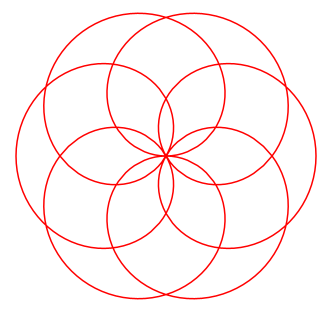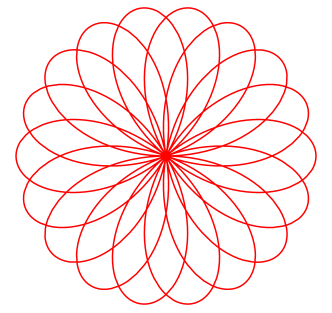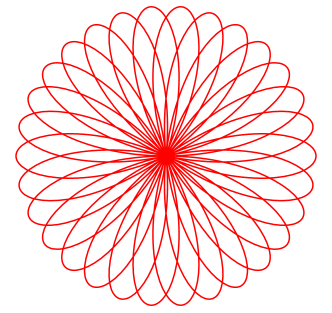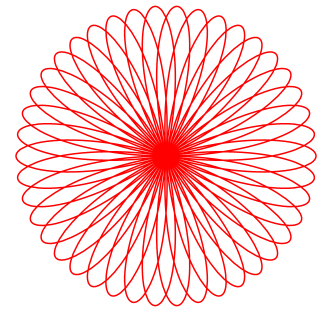
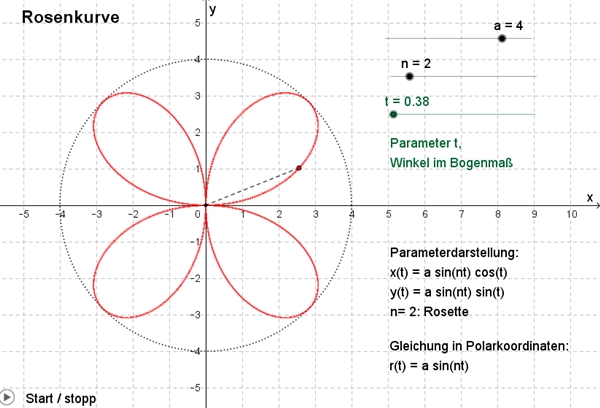
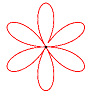
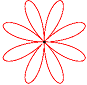
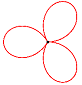
David Hilbert

Die Rosenkurven sind Kurven, die Ähnlichkeiten zu Blüten- und Kelchblättern von Blumen haben.

Ihre übliche Parameterdarstellung lautet:

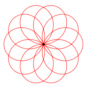
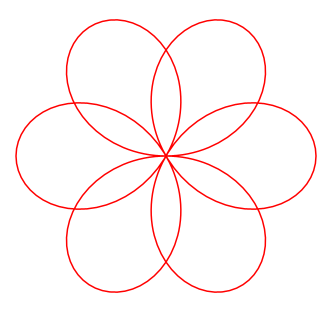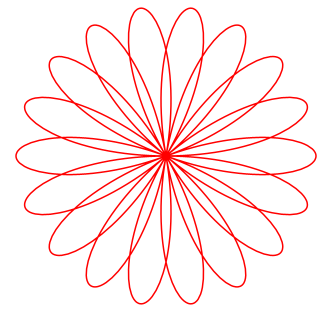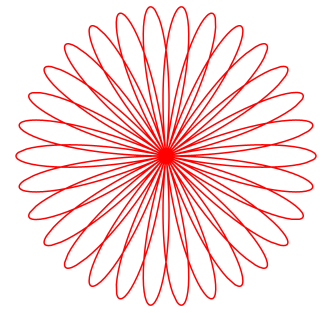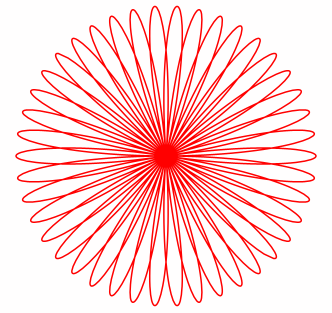
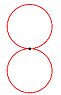
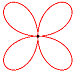
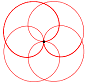
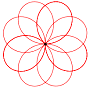
x(t) = a sin(n t) cos(t), y(t) = a sin(n t) sin(t), t = Winkel im Bogenmaß

a verändert die Größe der Kurve.

n verändert die Kurvenform.

Für unterschiedliche n ergeben sich z.B. folgende Kurven:

n = 1

n = 2

n = 3

n = 4

n = 1/2

n = 3/2

n = 5/2

n = 7/2

n = 1/3

n = 2/3

n = 4/3

n = 5/3

n = 1/4

n = 3/4

n = 5/4

n = 7/4

Animation und Variation von Rosenkurven

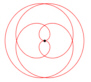
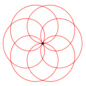
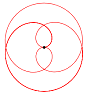
Folgende veränderte Parameterdarstellung würde zu einer besseren Systematik der Kurvenformen führen:

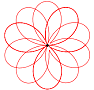
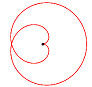
x(t) = a |sin(n t)| cos(t), y(t) = a |sin(n t)| sin(t), t = Winkel im Bogenmaß

Für unterschiedliche n ergeben sich z.B. folgende Kurven:

n = 1

n = 2

n = 3

n = 4

n = 1/2

n = 3/2

n = 5/2

n = 7/2

n = 1/3

n = 2/3

n = 4/3

n = 5/3

n = 1/4

n = 3/4

n = 5/4

n = 7/4

Animation einer Variation von Rosenkurven alternativ

Die Grafiken wurden mit GeoGebra erstellt.

Zurück
Zurück zur Startseite