Zykloide, Epizykloide, Hypozykloide und Lissajous-Figuren

Zykloiden 

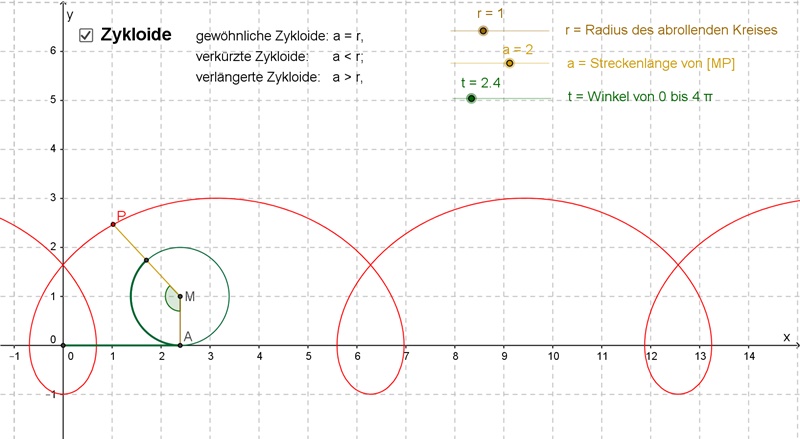
Rollt man einen Kreis auf einer Geraden ab, so beschreibt ein fester Punkt der Kreislinie eine (gewöhnliche) Zykloide.

Die Parameterdarstellung der Zykloide lautet allgemein:

x = r t - a sin(t),   y = r -a cos(t)

r =  Radius des rollenden Kreises

t = Winkel (Parameter), der für eine Periode die Zahlen von 0 bis 2 p durchläuft.

a = r :    gewöhnliche Zykloide

a > r :    verlängerte Zykloide

a < r :    verkürzte Zykloide

Zykloide animiert

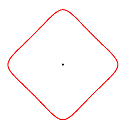
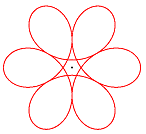
Epizykloiden

Rollt man einen Kreis auf einem zweiten Kreis außen ab, so beschreibt ein fester Punkt der Kreislinie eine (gewöhnliche) Epizykloide.

Die Parameterdarstellung der Epizykloide lautet allgemein:

x(t) = R cos(t) - a cos(R/r t),   y(t) = R sin(t) - a sin(R/r t)

r =  Radius des rollenden Kreises

t = Winkel (Parameter), der für eine Periode die Zahlen von 0 bis 2 p durchläuft.

a = r :    gewöhnliche Epizykloide

a > r :    verlängerte Epizykloide

a < r :    verkürzte Epizykloide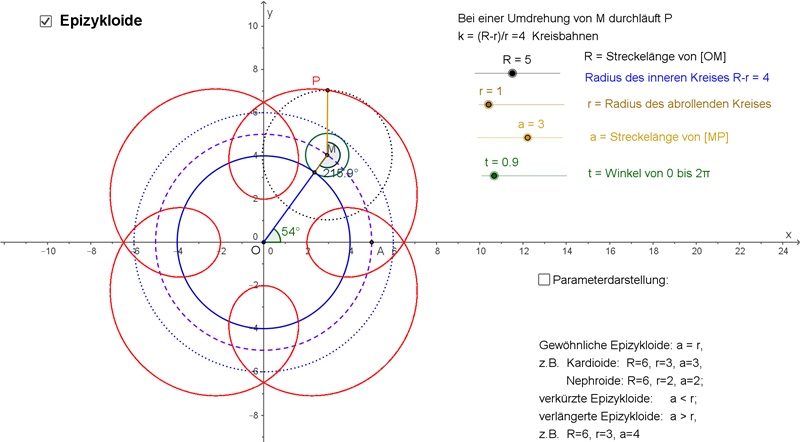

 

Epizykloide animiert

Sonderfälle:

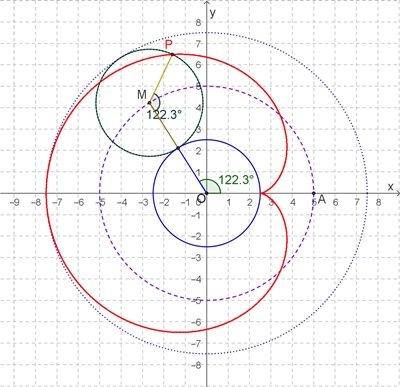
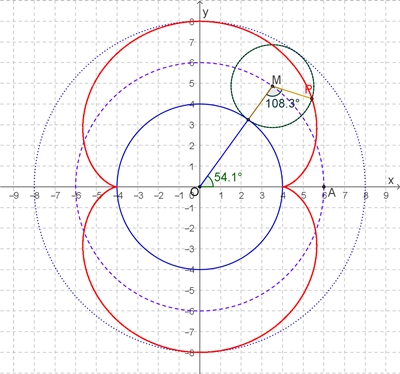
Kardioide                                                                        Nephroide

R = 2r,  r = a,  z.B. r = 2,5                                                R = 3r,  r = a,  z.B. r = 2

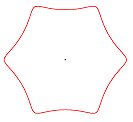
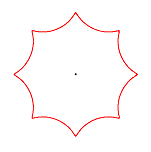
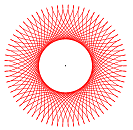
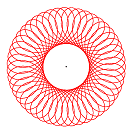
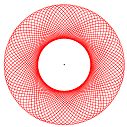
Hypozykloiden

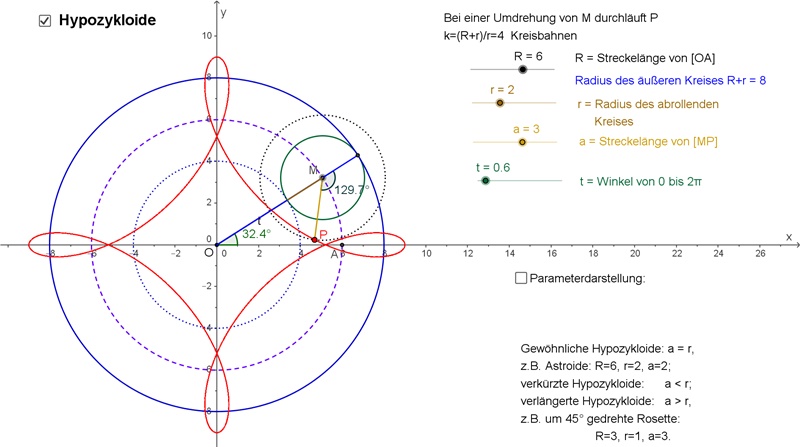
Rollt man einen Kreis auf einem zweiten Kreis innen ab, so beschreibt ein fester Punkt der Kreislinie eine (gewöhnliche) Hypozykloide.

Die Parameterdarstellung der Hypozykloide lautet allgemein:

x(t) = R cos(t) + a cos(R/r t),  y(t) = R sin(t) - a sin(R/r t) 

r =  Radius des rollenden Kreises

t = Winkel (Parameter), der für eine Periode die Zahlen von 0 bis 2 p durchläuft.

a = r :    gewöhnliche Hypozykloide

a > r :    verlängerte Hypozykloide

a < r :    verkürzte Hypozykloide  

Hypozykloide animiert

Eine Auswahl von Hypozykloiden:

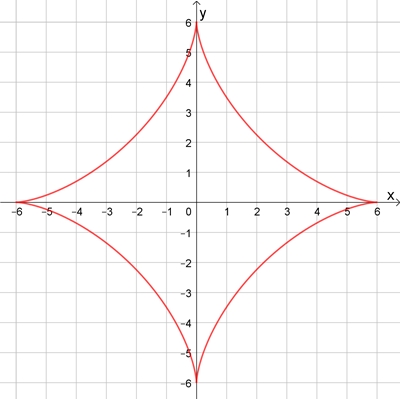
Die Astroide als spezielle Hypozykloide mit z.B. R = 4,5;  r = 1,5;  a = 1,5

Die Astroide entsteht auch als Hüllkurve von Ellipsen mit den Halbachsen a und b  und der Eigenschaft:  a + b = konstant, z.B. a + b = 6

Parameterdarstellung der Astroide mit t ϵ [0, 2π]:

x(t) = a (cos t)³,  y(t) = a (sin t)³ , hier:  a = 6

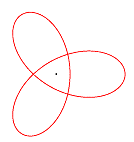
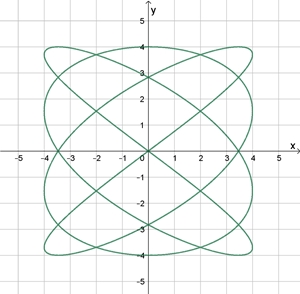
Lissajous-Figuren

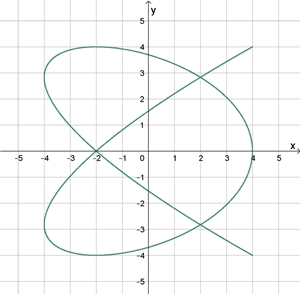
Lissajous-Figuren sind Kurvengraphen, die durch die Überlagerung zweier, rechtwinklig zueinander stehender Sinusschwingungen verschiedener Frequenz und Phase entstehen. 
Benannt sind sie nach dem französischen Physiker Antoine Lissajous (1822 – 1880)

Lissajous-Figuren können mit Hilfe eines Oszilloskops beim Anlegen von sinusförmigen Spannungen am x- und y-Eingang sichtbar gemacht werden.

Mit Hilfe von Geogebra können Lissajous-Figuren sehr schön in Abhängigkeit von den Parametern dargestellt werden.

Die Parameterdarstellung der Lissajous-Figur:

x(t) = a₁ sin(ω₁t + φ₁)

y(t) = a₂ sin(ω₂t + φ₂)

a₁ und a₂ sind die Amplituden der Sinusschwingungen in x- und y-Richtung

ω₁ und ω₂ sind die Frequenzen der Sinusschwingungen in x- und y-Richtung

φ₁ und φ₂ sind die Phasenverschiebungen der Sinusschwingungen in x- und y-Richtung

t t ϵ [0; 2π], bei nicht schließenden Kurven besser t ϵ [0; 16π].

Die Kurvenform wird bestimmt durch das Frequenzverhältnis ω₁ : ω₂, das Amplitudenverhältnis a₁ : a₂ und die Phasendifferenz Δφ = φ₁ – φ₂ der beiden Sinusschwingungen. Wenn das Verhältnis ω₁ : ω₂ rational ist erhält man eine geschlossene Kurve.

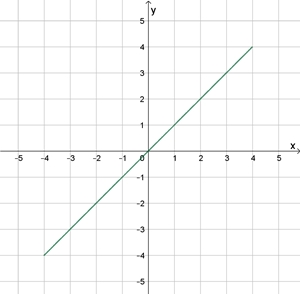
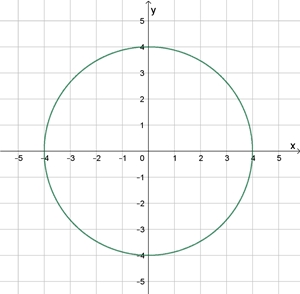
Lissajous-Figuren für φ₂ = 0

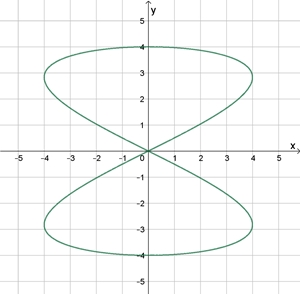
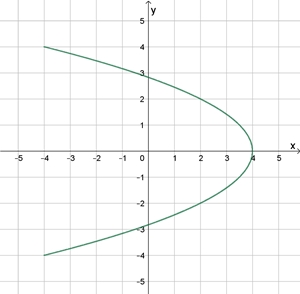
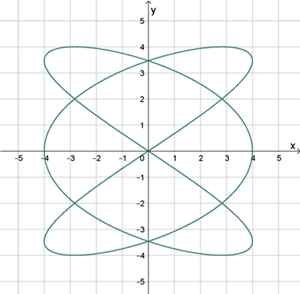
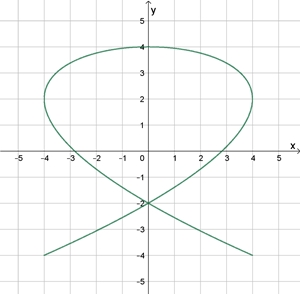
ω₁ : ω₂ = 1 : 1                                     ω₁ : ω₂ = 2 : 1                              ω₁ : ω₂ = 3 : 2                                  ω₁ : ω₂ = 4 : 3,    jeweils φ₁ = 0

ω₁ : ω₂ = 1 : 1, φ₁ = π/2,                   ω₁ : ω₂ = 2 : 1, φ₁ = π/2,               ω₁ : ω₂ = 3 : 2, φ₁ = π/4,                  ω₁ : ω₂ = 4 : 3,  φ₁ = π/2

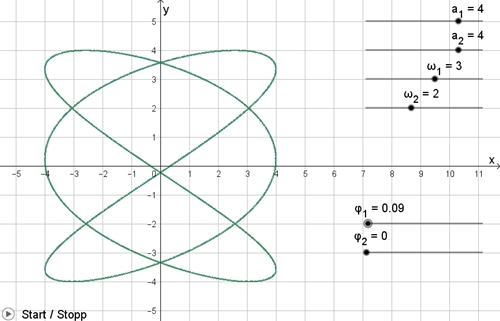
Animierte Darstellung von Lissajous-Figuren mit Variablen

Bei der Animation der Lissajous-Figur für variables φ₁ ϵ [0; 2π] entsteht der Eindruck einer Rotation der Figur.

Die Grafiken wurden mit GeoGebra erstellt.

Zurück
Zurück zur Startseite