Graphen und seine Anwendungen

Hände schütteln

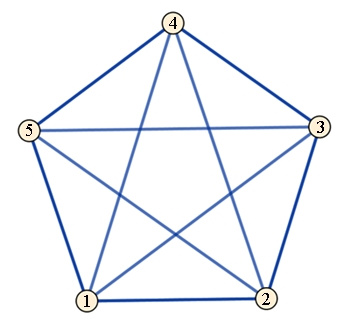
Wenn fünf Personen sich abends nach einem Party zum Aufbruch bereit machen, schüttelt jeder jedem anderen die Hand. Wie oft werden insgesamt die Hände geschüttelt?

 

Die Lösung kann durch einen vollständigen Graphen mit 5 Knoten dargestellt werden. Die Knoten stellen die Personen dar und die Kanten das Händeschütteln.

Es werden insgesamt 10 Händepaare geschüttelt.

Bei n Personen gilt:
1/2٠n٠(n-1) mal Händeschütteln.

 

   

Ein Graph mit n Knoten hat maximal 1/2٠n٠(n-1) Kanten.

 

Problem des Handlungsreisenden (Travelling Salesman Problem, TSP)

Die Aufgabe des Handlungsreisenden besteht darin, eine Reihenfolge für den Besuch mehrerer Orte so zu wählen, dass die Gesamtstrecke möglichst kurz wird. Dabei soll er jeden Ort nur einmal besuchen und dann zum Ausgangsort zurückkehren.

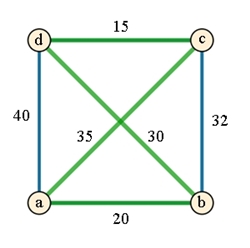
Beispiel: Graph mit 4 Orten a, b, c d

 

Startort beliebig,
3 mögliche Rundreisen (Hamilton-Kreise),
abcda, abdca und adbca,
kürzeste Gesamtstrecke:
abdca:  20 + 30 + 15 + 35 = 100

 

 

Für n Orte gibt es 1/2٠(n-1)! Möglichkeiten von Rundreisen.

Mit einer zunehmenden Anzahl von Orten wird die Anzahl der möglichen Rundreisen schnell sehr hoch, so dass bei 30 Orten und 1/2٠29! = 4420880996869850977271808000000 möglichen Rundreisen auch mit Hilfe eines Computers es schon sehr schwierig wird, den kürzesten Weg der Rundreise zu berechnen.

 

Paarungen (Matchings)

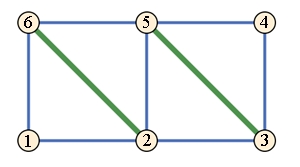
Die Paarung in einem Graphen ist die Teilmenge seiner Kanten, von denen keine zwei einen Knoten gemeinsam haben.

Beispiel:

  

Graph mit einer nicht erweiterbaren Paarung.
 Die Kanten {2,6} und {3,5} haben keine Knoten gemeinsam.

 

 

Gleicher Graph mit einer größtmöglichen (perfekten) Paarung.
 Die Kanten {1,6}, {2,3} und {4,5} haben keine Knoten gemeinsam.

 

Ein Graph mit 2n Knoten besitzt eine perfektes Paarung mit n Kanten, die keine Knoten gemeinsam haben.

  

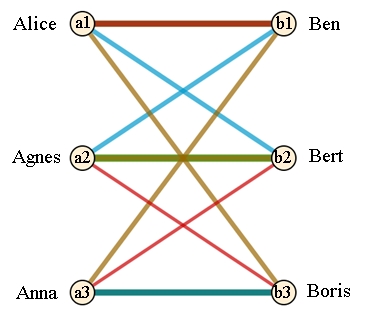
Wie viele Paare aus 3 Frauen und 3 Männern können gebildet werden?

Darstellung mit einem bipartiten Graphen

     

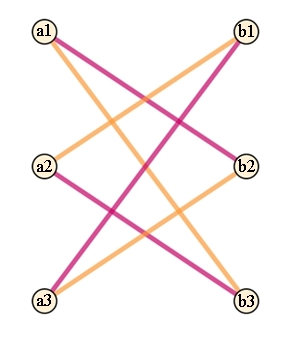
Die perfekte Paarung für einen bipartiten Graphen mit 2 mal 3-Knoten liefert 6 = 3! Kombinationen:

a1b1–a2b2–a3b3, a1b2–a2b1–a3b3,  a1b3–a3b1–a2b2,  a1b1–a2b3–a3b2,
a1b3–a2b1–a3b2,  a1b2–a2b3–a3b1
 

Die perfekte Paarung für einen bipartiten Graphen mit 2 mal n-Knoten liefert n! = 1٠2٠3٠…٠n  Kombinationen.

 

Briefträgerproblem

Eine Briefträgertour startet stets bei einer Straßenkreuzung, führt mindestens einmal durch jede Straße des Zustellbezirks und kehrt schließlich wieder zum Startpunkt zurück. Gesucht ist eine kürzeste Briefträgertour.

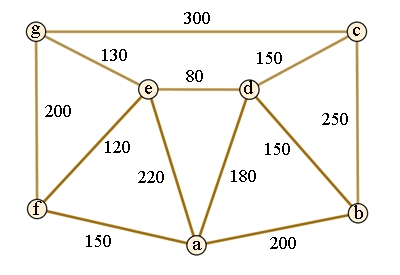
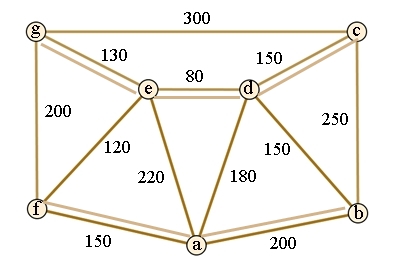
Beispiel:

Zu finden ist in dem gegebenen gewichteten zusammenhängenden Graphen eine Kantenfolge, die jede Kante mindestens einmal enthält und minimale Gesamtlänge hat. Zahlenangaben in m.

  

  

Da viermal 3 Kanten bei b, c, g und f ankommen kann der Briefträger die Tour nicht durchführen ohne Strecken zweimal zu gehen (Satz von Euler  und Hierholzer).

  

  

 

 

 

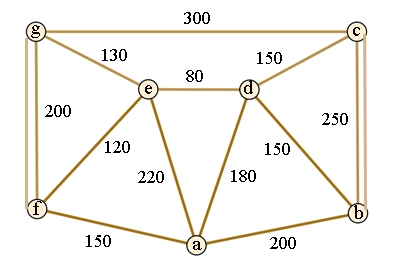
Eine Verdopplung von b-c und f-g bringt die Lösung eines geschlossenen Weges von  insgesamt 2580 m, Startpunkt gleich Zielpunkt ist beliebig,

   

   

 

 

 

mögliche 2. Lösung liefert hier keinen kürzeren Gesamtweg.

 

   

 

 

Kabelnetz

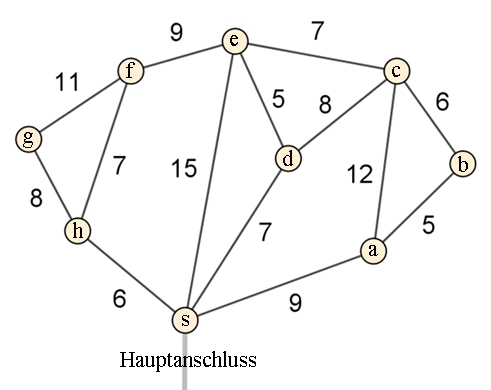
In einem Wohngebiet sollen Glasfaserkabel verlegt werden.

  

Bei dem Graphen werden Kabelleitungen durch Kanten und die Häuser durch Knoten von a bis h und der Anschlussknoten mit s dargestellt.

Die veranschlagten Kosten der einzelnen Kabelabschnitte sind in tausend Euro angegeben.

  

 

 

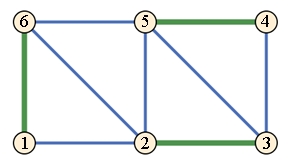
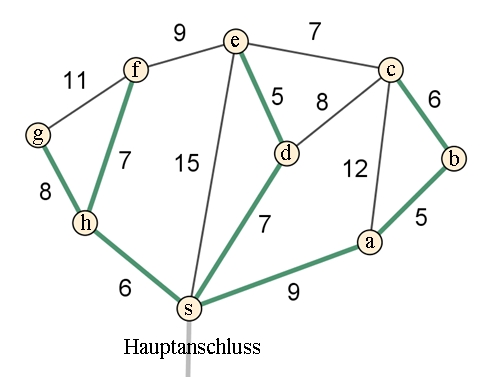
Gesucht ist die billigste Verkabelung, die an die Hauptleitung anschließt.

 

Das Ergebnis ist ein aufgespannter Baum (Spannbaum) mit den grünen Kanten

6+8+7 + 7+5 + 9+5+6 = 53

Gesamtkosten: 53 000 €

 

 

 

Netzwerk eines Rohrsystems

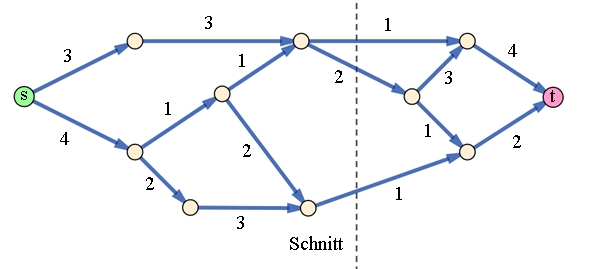
Beispiel:

Durch ein Netz aus Wasserleitungen soll möglichst viel Wasser vom Anfangsknoten s (source) zum Endknoten t (target) gepumpt werden.

Die Zahlen geben den jeweiligen maximalen Durchfluss der jeweiligen Röhre, dargestellt durch eine gerichtete Kante.

 

Ein Schnitt durch das Netzwerk zeigt den maximal möglichen Durchfluss 1 + 2 + 1 = 4 (minimaler Wert der Summe eines Schnittes) an. 

In diesem Netzwerk können z.B. höchstens vier Einheiten Wasser pro Zeiteinheit vom  Anfangsknoten s bis zum Endknoten t transportiert werden.

 

  

Weitere Beispiele von Graphen

Das Internet ist ein riesiger virtueller Graph. Die Knoten sind die einzelnen Webseiten, und die Kanten sind die Hyperlinks zwischen zwei Seiten.

Ein Netzwerk aus Computer, Servern, Routern (Knoten) und Leitungen (Kanten).

Graphen spielen auch im Transport- und Verkehrswesen eine wichtige Rolle. Alle Flug-, Zug- und U-Bahn-Netze bilden Graphen, die bei der Erstellung effizienter Fahrpläne genutzt werden.

Navigationssoftware bildet ein Netzwerk aus Straßen und Autobahnen, um die kürzeste Route zwischen zwei bestimmten Orten zu ermitteln.

Die Verbindungen zwischen Atomen und Molekülen bilden einen Graphen

Die Evolutionsbäume in der Biologie, die die Abstammung der Arten zeigen, bilden einen Graphen.

Soziale Netzwerke zwischen Menschen und deren Beziehungen.

   

Zurück
Zurück zur Startseite