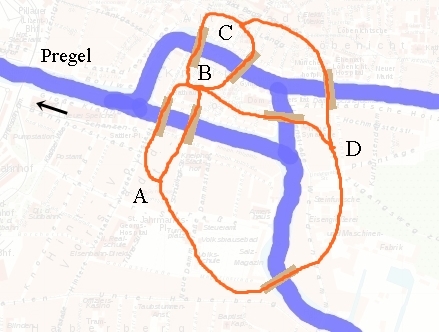
Das Königsberger Brückenproblem von Leonhard Euler (1707 – 1783)

Kann man bei einem Spaziergang durch Königsberg (seit 1946 Kaliningrad) im Jahr 1735 jede der Brücken über die Pregel genau einmal überqueren fragte sich Leonard Euler und präsentierte dann eine Lösung des Problems durch die Veröffentlichung der Arbeit Solutio problematis ad geometriam situs pertinentis.

In jedem Stadtteil von Königsberg soll es einen Punkt geben, in dem sich die roten Spazierwege treffen.

Zur Vereinfachung sollen die Wege elastisch sein, die man beliebig dehnen und stauchen kann.

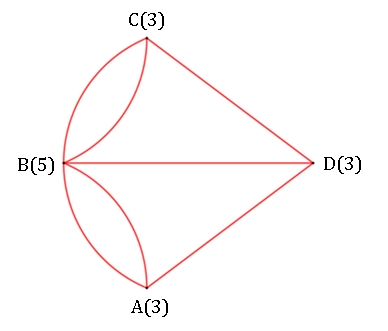
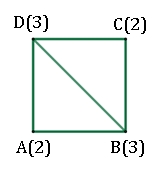
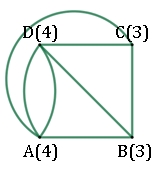
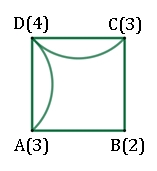
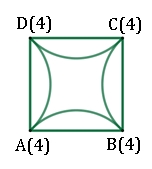
So erhält man z.B. folgende Figur aus Strecken und Bögen (Kanten) und Punkten (Knoten), die man Graph nennt.

In Klammern wird hinter jedem Punkt die Anzahl der Linien angegeben, die in diesem Punkt zusammentreffen.

Ergebnis:

Es gibt keinen Weg der den Graph ohne Überschneidung durchläuft.

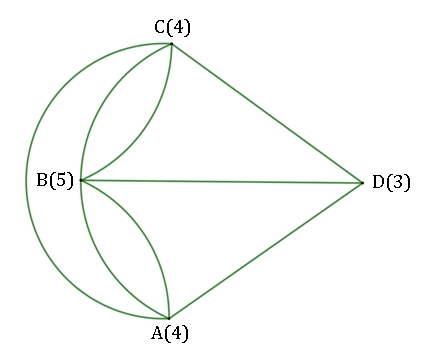
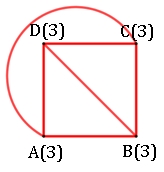
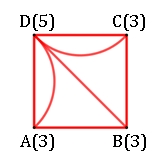
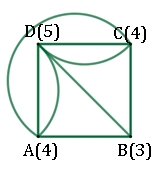
Später wurde in Königsberg flussabwärts eine Eisenbahnbrücke gebaut, so dass ein weiterer Bogen hinzukommt.

Ergebnis:

Es gibt einen Weg mit Anfangspunkt B und Endpunkt D oder Anfangspunkt D und Endpunkt B, welcher den Graphen durchläuft.

Graphen mit 4 Ecken:

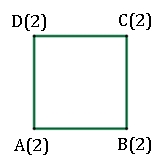
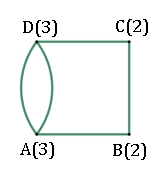
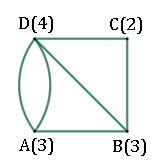
Die Graphen mit 4 Ecken können genau dann in einem Weg durchlaufen werden, wenn die Anzahl der Linienenden in einer Ecke jeweils gerade ist oder wenn die Anzahl Linienenden zweier Ecken jeweils ungerade ist.

Allgemein gilt (Satz von Euler 1735 und Hierholzer 1873):

(a)          Wenn ein zusammenhängender Graph keine Ecken mit einer ungeraden Anzahl von Linienenden hat, kann es stets von einem einzigen Weg durchlaufen werden.

(b)          Wenn ein zusammenhängender Graph genau zwei Ecken mit einer ungeraden Anzahl von Linienenden besitzt, kann er von einem einzigen Weg durchlaufen werden, dessen Anfangs- und Endecke die beiden ungeraden Ecken des Netzes sind.

Regensburger Brückenproblem (ohne Eisenbahn- und Ostbrücke)

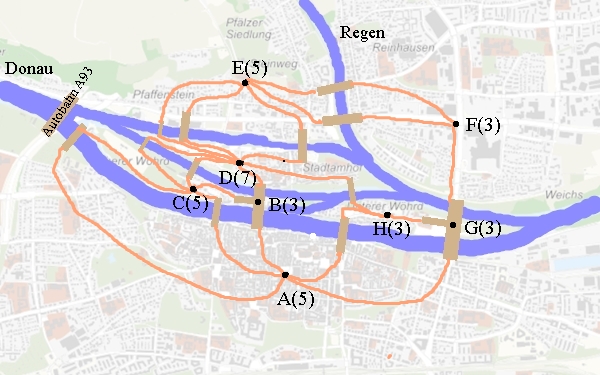
Es gibt keinen zusammenhängenden Weg, bei dem über die Brücken der Donau und des Regens nur einmal gegangen werden kann, da die Eckenzahl des zugehörigen Graphen jeweils ungerade ist.