Graphen, Bezeichnungen und Eigenschaften

Graphen sind mathematische Modelle für netzartige Strukturen.

Anschaulich besteht ein Graph in der Graphentheorie aus einer Menge von Punkten, zwischen denen Linien verlaufen.
Die Punkte nennt man Knoten oder Ecken, die Linien nennt man Kanten. Die Linien sind dabei beliebig dehnbar. 

Ein Graph G ist ein Paar (V, E), wobei E die Menge der Knoten (engl. vertices) des Graphen ist und  E die Menge der Kanten (engl. edges) von G ist.
Zwei Knoten, die durch eine Kante verbunden sind, heißen benachbart (adjazent).

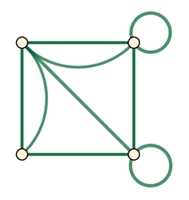
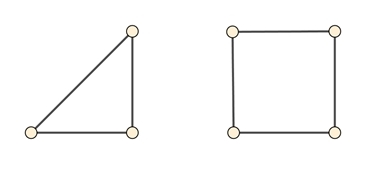
Einfache Graphen und Multigraphen

 Ein einfacher Graph besitzt zwischen zwei Knoten höchstens eine Kante.

Bei einem Multigraphen können zwei Knoten auch durch mehrere Kanten verbunden sein und Schlingen besitzen.

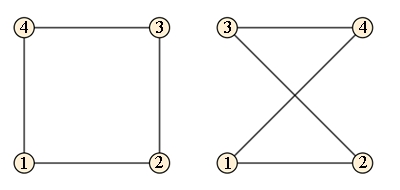
Ungerichtete, gerichtete und gewichtete Graphen

Bei einen ungerichteten Graphen können die Kanten in beiden Richtungen durchlaufen werden.

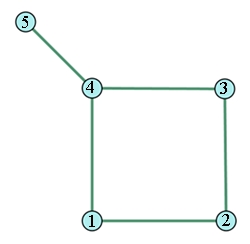
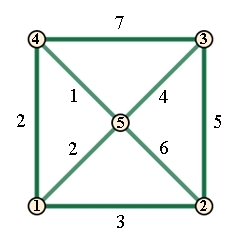
Beispiel:

Menge der Knoten V = {1, 2, 3, 4, 5}

Menge der Kanten E = {{1,2}, {2,3}, {3,4}, {1,4}, {4,5}}

{1,2} bedeutet, dass die Reihenfolge keine Rolle spielt

Der Grad eines Knotens gibt die Anzahl der vom Knoten ausgehenden Kanten an,
z.B. Knoten 4 hat Grad 3, i.Z.  4(3)

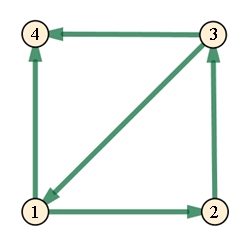
Bei einem gerichteten Graphen können die Kanten nur in einer Richtung (Pfeilrichtung) durchlaufen werden.

Beispiel:

Menge der Knoten V = {1, 2, 3, 4}

Menge der Kanten E = {(1,2), (2,3), (3,1), (1,4), (3,4)}

(1,2) bedeutet Reihenfolge 1 dann 2

Ein gewichteter Graph ordnet jeder Kante k eine nichtnegative reelle Zahl w(k) (Gewicht von k) zu,
z.B. w({2,3}) = 5

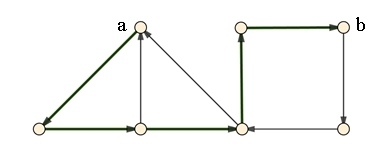
Zusammenhängende und unzusammenhängende Graphen

Beispiele:

Ein nicht zusammenhängender Graph.

Ein ungerichteter Graph heißt zusammenhängend, wenn es zu je zwei beliebigen Knoten a und b einen Weg von a nach b gibt.

Ein gerichteter Graph heißt zusammenhängend von einem Knoten a aus, wenn es zu jedem anderen Knoten b einen gerichteten Weg von a nach b gibt.

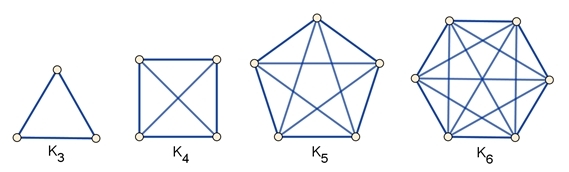
Vollständige Graphen

Bei einem vollständigen Graphen werden je zweie Knoten durch eine Kante verbunden.

Z.B. der vollständige Graph  K₅ hat 5 Knoten und 5٠4 / 2 = 10 Kanten.

Allgemein gilt:

Ein vollständiger Graph  K_n​ mit n Knoten ist ein ungerichteter Graph ohne Mehrfachkanten und hat genau    Kanten für n>1. Die Diagonalen bilden keine Knoten als Schnittpunkte (räumliches Fünfeck).

Ein vollständiger Graph K_n​ kann durch ein n-Eck mit allen seinen Diagonalen dargestellt werden.

Azyklische Graphen: Weg (Pfad), Baum, Wald

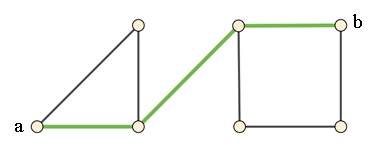
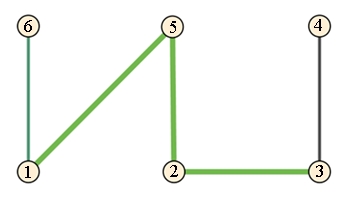
Weg, Beispiel:

    Graph W mit Knotenmenge V = {1, 2, 3, 5}

und Kantenmenge E = {{1,5}, {2,3}, {2,5}}

Kantenfolge: 1–5–2–3

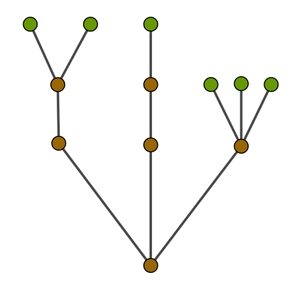
Baum, Beispiel:

Die grünen Knoten heißen Blätter,
die übrigen braunen Knoten heißen innere Knoten

Der Graph ist zusammenhängend und die Anzahl der Knoten ist um 1 größer als die Anzahl der Kanten.

 
Wald, Beispiel:

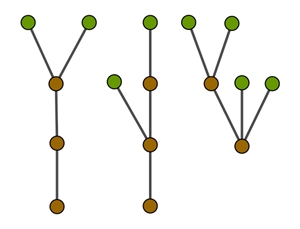
Der Wald besteht aus nicht zusammenhängenden Bäumen..

Zyklische Graphen: Zyklus, Kreis, vollständiger Graph

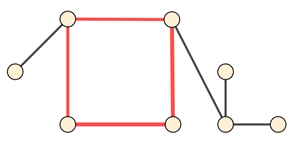
Beispiel: Kreis

Ein Graph ist ein Zyklus, wenn Anfangsknoten und Endknoten einer Kantenfolge gleich sind.

Ein Graph ist ein Kreis, wenn alle Knoten einer geschlossenen Kantenfolge verschieden sind.
Ein Kreis ist ein geschlossener Weg.

Die roten Kanten bilden mit den zugehörigen Knoten einen Kreis.

Ein vollständiger Graph ist ein zyklischer Graph.

Bipartite Graphen 

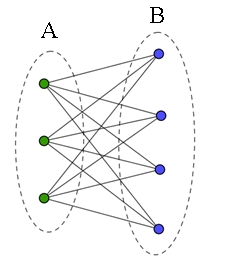
Ein vollständiger bipartiter Graph  K_n,m​ mit n Knoten aus einer Menge A und m Knoten aus einer Menge B ist ein ungerichteter Graph, der alle Knoten aus der Menge A mit allen Knoten aus der Menge B verbindet.

Der vollständige bipartite Graph  K_n,m​ hat n٠m Kanten. 

Beispiel:

K_3,4  hat 3٠4 = 12 Kanten

Planare Graphen

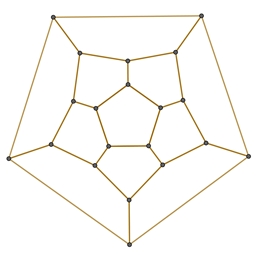
Ein Graph heißt planar, falls er so in die Ebene gezeichnet werden kann, dass sich verschiedene Kanten nicht kreuzen, das heißt, nur in Knoten berühren, z.B. Dodekaeder-Graph.  

Ein planarer Graph G = (V, E, R) zusammen mit einer planaren Repräsentation in die Ebene heißt ebener Graph. R bezeichnet dabei die Gebiete (engl. regions) von G in der gegebenen Einbettung.

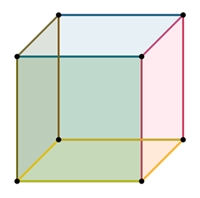
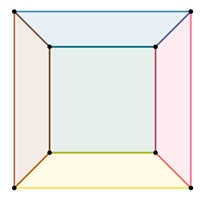
Hexaeder (Würfel) im Schrägbild           planarer Graph des Hexaeders

Die Rückseitenfläche des Würfels wird zur Außenfläche des Hexaeder-Graphen.

Leonard Euler (1707 – 1783)  bewies 1752 die nach ihm benannte Polyederformel:
|V|−|E|+|R|= 2.
{\displaystyle E=} V = Anzahl der Ecken,  E = Anzahl der Kanten,  R = Anzahl der Flächen.

Für jeden ebenen Graphen gilt ebenso |V|−|E|+|R|= 2, wenn die Außenfläche der eingeschlossenen Fläche auch als Fläche zählt.

Beim Hexaeder-Graphen gilt dann:  |V| = 8, |E| = 12, |R| = 5+1, 8 – 12 + 6 = 2

Beim Dodekaeder-Graph gilt:
|V| = 20, |E| = 30, |R| = 11+1, 20 – 30 + 12 = 2

Eulersche und Hamiltonsche Graphen

Eine geschlossene Kantenfolge, die jede Kante von G mindestens einmal enthält, heißt Tour.
Ein Kantenzug in G, der jede Kante von G genau einmal enthält, heißt Eulerscher Kantenzug.
Ein geschlossener Eulerscher Kantenzug heißt Eulersche Tour oder Eulerkreis und ein Graph mit einer Eulerschen Tour heißt Euler-Graph.

Satz von Euler und Hierholzer

Sei G = (V,E) ein zusammenhängender ungerichteter Graph, k1, k2 ∈ V mit k1 ≠ k2.

(a)  G ist genau dann Euler-Graph (Eulersch), wenn der Grad jedes Knoten gerade ist.

(b)  G hat genau dann einen Eulerschen Kantenzug von k1 nach k2, wenn k1 und k2 die einzigen Knoten mit ungeradem Grad sind.

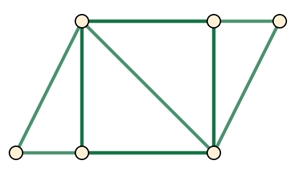
Räumliche n-Ecke mit ungeradem n erfüllen die Bedingung (a) des Satzes von Euler und Hierholzer (alle Knoten haben eine gerade Anzahl von Kanten) und bilden einen geschlossenen Eulerkreiszug,

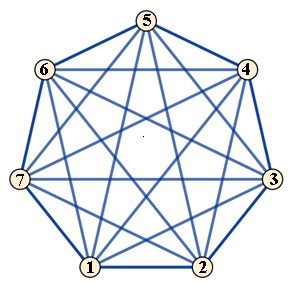
z.B. Siebeneck, von jedem Knoten gehen 4 Kanten aus, die sich nicht in einem Knoten schneiden (räumliches Siebeneck, kein planarer Graph).

Ein Hamilton-Kreis ist ein geschlossener Pfad in einem Graphen, der jeden Knoten genau einmal enthält. Der zugehörige Graph heißt Hamiltonscher Graph.

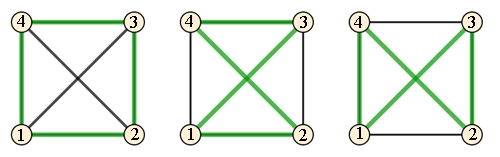
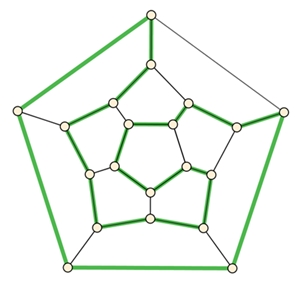
Die 3 Hamilton-Kreise im vollständigen Graphen K₄ 12341, 12431, 14231  und ein Hamilton-Kreis in einem Dodekaeder-Graph.

Isomorphie von Graphen

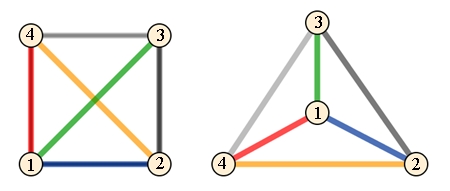
Zwei Graphen heißen isomorph, wenn nur ihre Kanten gestaucht oder gedehnt werden.
Sie sind dann gleichwertig.

Die beiden Graphen sind isomorph, wobei der 2. Graph ein planarer Graph ist.

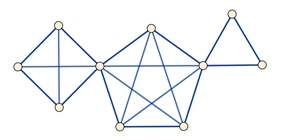
Cliquen

Beispiel:

Cliquen sind Teile eines Graphen, bei denen die Knoten miteinander vollständig mit Kanten verbunden sind.

Im Beispiel sind 3 Cliquen dargestellt.

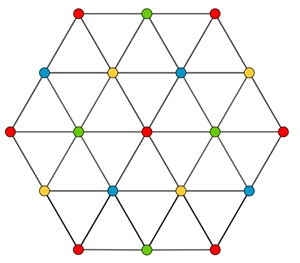
Graph des Vierfarbenproblems

Wie viele Farben man braucht man, um die Länder einer Landkarte einzufärben, sodass keine zwei benachbarten Länder die gleiche Farbe zugewiesen bekommen. Die Nachbarschaftsbeziehung der Länder kann man als Graph darstellen. Dabei werden die Länder durch Knoten dargestellt.

Das Problem kann als Knoten-Färbungsproblem dargestellt werden.
Nach dem Vier-Farben-Satz braucht man maximal vier verschiedene Farben. 

 
Fluss in Netzwerken

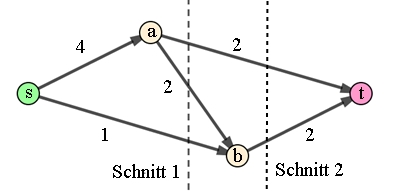
Das Netzwerk besteht aus einem gerichteten Graphen G = (V, E) mit zwei besonderen Knoten, der Quelle s (engl. source) und der Senke t (engl. target), wobei jeder Kante e ϵ E eine nichtnegative Zahl u(e) als Flusswert (Kapazität) zugewiesen wird.

Die Kapazität des Flusses ist die minimale Summe eines Schnittes.

Beispiel:                                                                            

Schnitt 1 liefert als Kapazität 1 + 2 + 2 = 5,

Schnitt 2 liefert als Kapazität 2 + 2 = 4

Die Kapazität des Flusses ist auf 4 begrenzt.

Kommunikationsnetzwerke

Kommunikationsnetzwerke lassen sich gut durch verschiedene Graphen mit Knoten und Kanten darstellen. Die Knoten entsprechen den Stationen, die Kanten den Wegen der Datenübertragung.

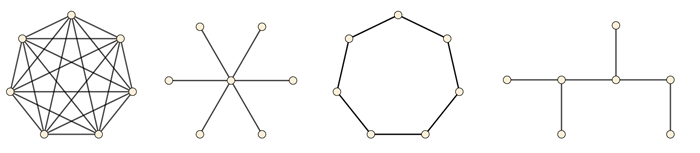
In der folgenden Abbildung sind vier Grundstrukturen gebräuchlicher Netzwerke dargestellt.

Vollständiger Graph   Sternstruktur        Ringstruktur        Busstruktur

Vollständiger Graph (Vollvermascht):

Jeder Knoten steht mit jedem Knoten in Verbindung.

Sternstruktur:

Verbindungen bzw. Daten laufen über einen zentralen Knoten.

Ringstruktur:

Es gibt keine zentralen Knoten, alle Stationen sind gleichberechtigt. Jeder Teilnehmer (Knoten) ist mit dem linken und rechten Partner (Knoten) verbunden.

Busstruktur

Es gibt keinen zentralen Knoten. Die Verbindung zu allen Teilnehmern erfolgt über einen gemeinsamen Übertragungsweg. 

Weitere Strukturen sind durch unvollständige Graphen gegeben.