Die geometrische Reihe

Eine geometrische Folge ist eine regelmäßige mathematische Zahlenfolge mit der Eigenschaft, dass das Verhältnis zweier benachbarter Folgenglieder konstant ist. Das n-te Glied a_n einer geometrischen Folge mit dem Anfangsglied a und dem Quotienten q berechnet sich aus 

:

a₁ = a,  a₂ = aq,  a₃ = aq²,  a₄ = aq³, …

Eine geometrische Reihe ist die Folge, deren n-tes Glied die Summe der ersten n Glieder der zugehörigen geometrischen Folge ist:

s_n =  a + aq + aq² + aq³ + …+ aq^n-1 .

Formel zur Berechnung der geometrischen Reihe

Herleitung:

I           s_n =  a + aq + aq² + aq³ + …+ aq^n-1

II       s_n q =  aq + aq² + aq³ + aq⁴ + …+ aqⁿ

I-II   s_n - s_n q =  a - aqⁿ

         s_n (1- q) =  a (1- qⁿ)

Formel:     

Eine unendliche geometrische Reihe entsteht, wenn bei der geometrischen Reihe n gegen Unendlich geht:

Für |q| < 1 gilt:      für    .

Dann ergibt sich als Grenzwert für die unendliche geometrische Reihe:

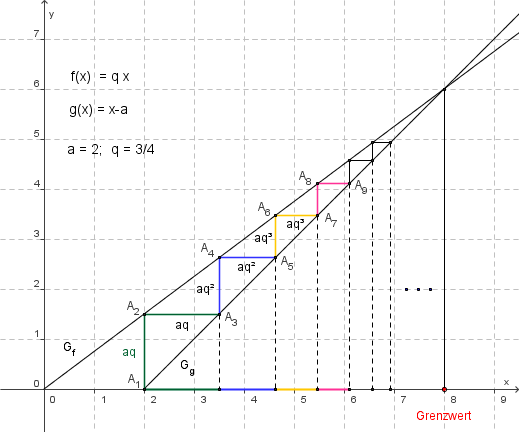
Beispiel:   

Für a = 2 und q = 0,75 ergibt sich als Grenzwert 8.

Dies lässt sich an Hand folgender graphischen Darstellung veranschaulichen:
  

Die Treppenlinie zwischen den Graphen der Funktionen mit den Gleichungen f(x) = 0,75 x und  g(x) = x -2 besitzt folgende Eigenschaften:

1. Die Dreiecke A₁A₂A₃, A₃A₄A₅, A₅A₆A₇, ... sind alle gleichschenklig rechtwinklig und haben damit gleiche Kathetenlängen. 

2. Die Dreiecke OA₁A₂, A₂A₃A₄, A₄A₅A₆, ... besitzen die Steigung q als Quotient zwischen senkrechter und waagrechter Kathetenlänge.

3. Die senkrechten Projektionen der waagrechten Katheten auf die x-Achse stellen die Glieder der geometrischen Reihe dar.

4. Die Summe der projizierten Streckenlängen liefert als Grenzwert den Wert 8.

Graphische Veranschaulichung dynamisch

Zurück
Zurück zur Startseite