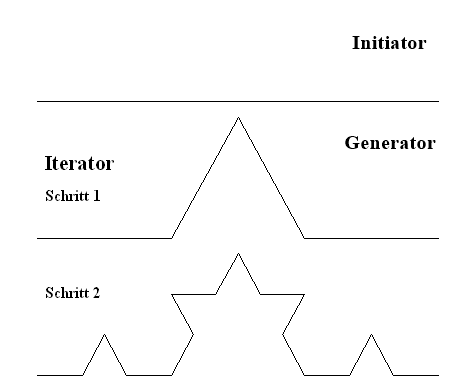
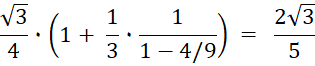Koch-Schneeflocke - Grenzwert1) Die Kochkurve Die Koch-Kurve ist ein von dem schwedischen Mathematiker Helge von Koch 1904 entdecktes Beispiel für eine überall stetige, aber nirgends differenzierbare Kurve. Sie stellt außerdem ein Fraktal dar. Die Koch-Kurve wird durch eine Iteration folgendermaßen beschrieben: Zunächst sei eine Strecke mit vorgegebener Länge gegeben (Generator). Dann entfernt man das mittlere Drittel der Strecke und errichtet darüber ein gleichseitiges Dreieck mit der Länge der entfernten Strecke (Iterator). Im nächsten Schritt wird der Iterator auf jeden der vier entstandenen Streckenabschnitte angewandt. Diese Iteration wird nun beliebig oft wiederholt.
2) Die Koch-Schneeflocke
Die Kantenlänge des
gleichseitigen Dreiecks sei 1. Der Umfang der nachfolgenden
Koch-Schneeflocke verlängert sich bei jedem Schritt um den Faktor 4/3.
Daher geht der Umfang der n-ten Koch-Schneeflocke für
n → ∞
gegen Unendlich.
Im n-ten Schritt werden
3٠4n-1
gleichseitige Dreiecke mit
Kantenlänge
3-n und Fläche
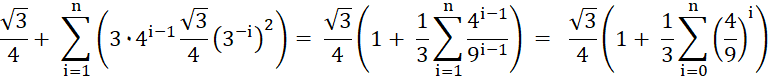 Für n → ∞ ergibt sich als Grenzwert für den Flächeninhalt unter Anwendung der Formel für die geometrischen Reihe:
Ergebnis: Für n → ∞ besitzt die Koch-Schneeflocke einen endlichen Flächeninhalt und wird von einer unendlich langen Kurve umschlossen!
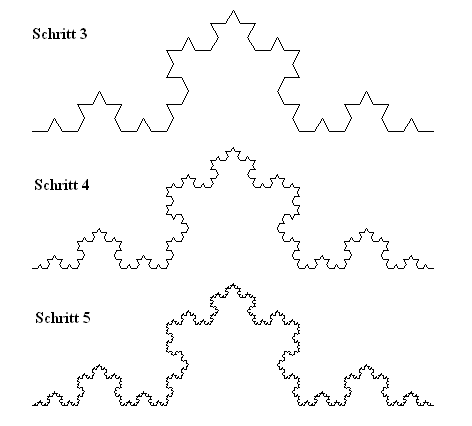
Die verschiedenen Schritte einer expandierenden Koch-Schneeflocke in
einem Bild:
Stilisierte Schneeflocken
|
![\includegraphics[width=\textwidth]{kochbilder.eps}](koch-sfl1.gif)
![\includegraphics[width=\textwidth]{kochbilder.eps}](koch-sfl2.gif)