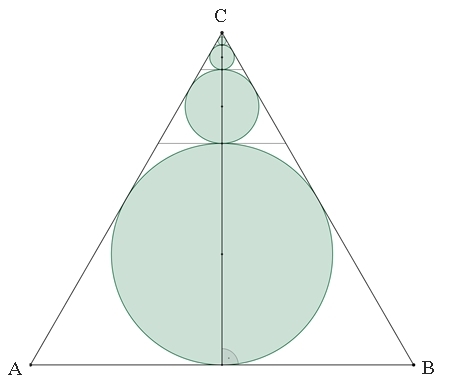
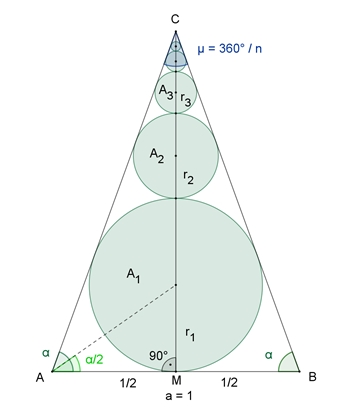
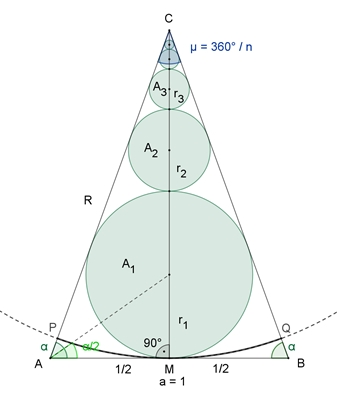
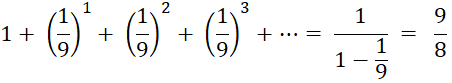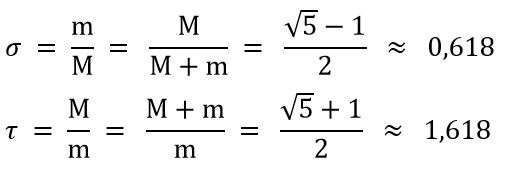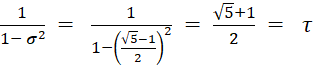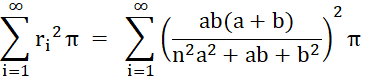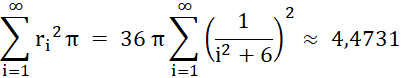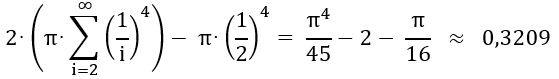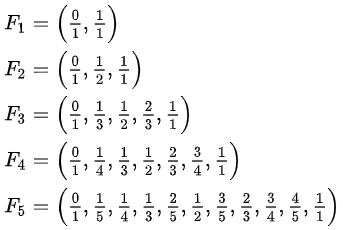KreiskettenKreiskette im Dreiecka) Kreiskette im gleichseitigen Dreieck Einem gleichseitigen Dreieck der Seitenlänge 1 werden Kreise folgendermaßen einbeschrieben:
Berechnung der Summe der Flächeninhalte aller einbeschriebenen Kreise. Die einzelnen Kreise entstehen
jeweils durch zentrische Streckung mit dem Zentrum C und dem Streckungsfaktor
1/3 aus dem unteren Kreis mit dem Radius
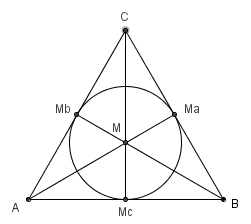
Begründung: Im
gleichseitigen Dreieck ist der Höhenschnittpunkt gleich dem Schnittpunkt der
Seitenhalbierenden gleich dem Schnittpunkt der Winkelhalbierenden
(Inkreismittelpunkt); der Schnittpunkt der Seitenhalbierenden teilt diese im Verhältnis
2 : 1;
Die Radien der Kreise sind
Die Summe aller Kreisflächeninhalte ergibt dann folgende unendliche Reihe:
NR: Geometrische Reihe:
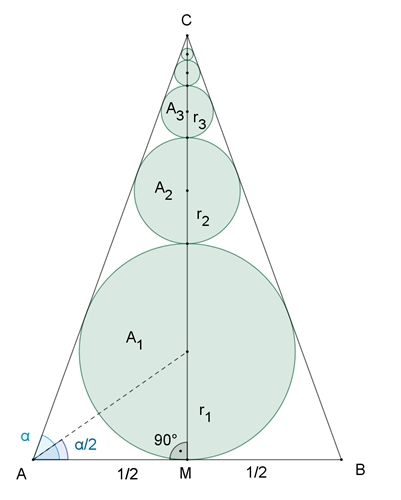
b) Kreiskette im gleichschenkligen Dreieck
h = |MC| = ½⸱tan(α)
r1
= ½٠tan(α/2),
r2
= x
r1
: x = (h – r1)
: (h – 2 r1
– x) (Strahlensatz)
Nach Vereinfachung mit CAS folgt:
x = sin(α)(1
– cos(α))
/ (2(cos(α))2
+ 2cos(α)
+ 1)
Für das Verhältnis v = r2
/ r1
ergibt sich:
v = (sin(α))2
/ (1 + cos(α))2
= (tan(α/2))2
Für das Verhältnis der Kreisflächen A2
und A1 ergibt sich dann
A2
/ A1
= (tan(α/2))4
Entsprechend gilt:
A2
/ A1
= A3
/ A2
= A4
/ A3
= …
Daraus folgt für die Summe A aller Kreisflächen mit
A1
= (½ tan(α/2))2
π:
A = (1/2٠tan(α/2))2
π (1 + (tan(α/2))4
+ (tan(α/2))8
+ (tan(α/2))12
+ … )
Für α
= 60° ergibt sich: A = π/12 ٠ 9/8 = 3π/32 ≈ 0,2945 (siehe
1a)
Das sind ungefähr 68,0% der Dreiecksfläche.
Für α
= 70° ergibt sich: A ≈ 0,3851 ٠ 1,3165 ≈ 0,5069
Das sind ungefähr 73,8% der Dreiecksfläche.
Für α
= 76,345° ergibt sich:
A ≈
0,4854 ٠ 1,6180 ≈ 0,7854
Das sind ungefähr 76,9% der Dreiecksfläche.
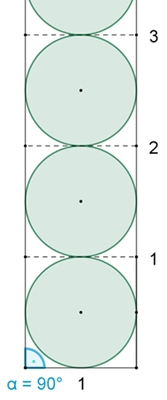
Für α
→ 90° nähert sich der Flächenanteil der Kreisflächen im
Vergleich zur Dreiecksfläche dem Wert π/4 ≈ 78,54%. Begründung: Für α = 90° werden aus den gleichlangen Schenkeln des Dreiecks zwei parallele Halbgeraden, wie in nebenstehender Figur dargestellt.
Der Kreisflächenanteil ist bei einem Kreis mit umschriebenem Quadrat
π/4.
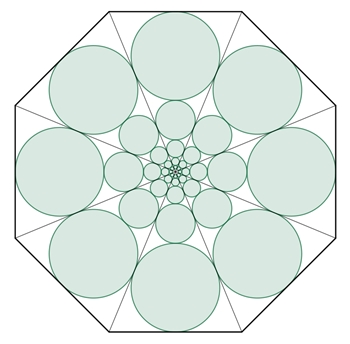
Kreisketten im regulären n-Eck
n-Eck-Sektor:
Summe der Kreisflächeninhalte
(s. oben)
A = (1/2٠tan(α/2))2 π (1 + (tan(α/2))4 + (tan(α/2))8 + (tan(α/2))12 + … )
Dreiecksflächeninhalt D des Dreiecks
ABC
Flächenverhältnis A/D
A/D = (tan(α/2))2 π
(1 + (tan(α/2))4 + (tan(α/2))8 + (tan(α/2))12 +
… ) / tan(α)
Tabelle der
Flächenverhältnisse A/D
Wenn n gegen Unendlich geht,
geht das Flächenverhältnis A/D gegen
78,5%.
Dieselben
Flächenverhältnisse gelten für das reguläre n-Eck, das aus n n-Eck-Sektoren
besteht.
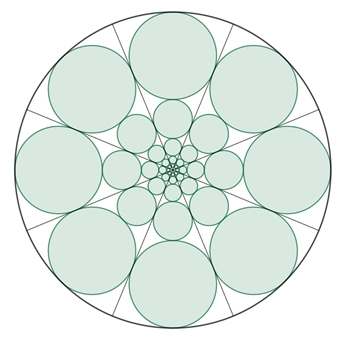
Kreisketten im Kreis
Kreissektor 360°/n:
Summe A der
Kreisflächeninhalte
(s. oben)
A = (1/2٠tan(α/2))2 π (1 + (tan(α/2))4 + (tan(α/2))8 + (tan(α/2))12 + … )
Kreisflächenflächeninhalt K
K = R2 π
R / 0,5 = tan(α)
K = (1/2٠tan(α))2 π
Flächenverhältnis nA/K:
nA/K
= n (tan(α/2))2 (1 + (tan(α/2))4 +
(tan(α/2))8 + (tan(α/2))12 + … )
/ (( tan(α))2 π) mit α = 90°
– 360°/2n =
π/2
–
π/n
(180° =
π)
Tabelle der
Flächenverhältnisse nA/K
Wie beim n-Eck geht
für n gegen Unendlich das Flächenverhältnis nA/K gegen
78,5%.
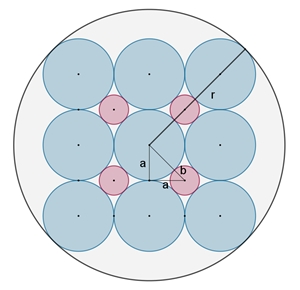
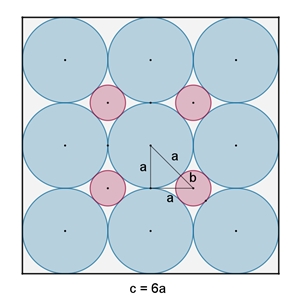
Kreise in quadratischer Anordnung im Kreis und im
Quadrat Die Flächeninhalte der n² blauen Kreise sei Kb, der (n–1)² roten Kreise Kr, des Umfangskreises Ku, des Quadrats Q.
Für das Verhältnis der Flächeninhalte der blauen und roten Kreise zusammen
zum Umkreis gilt für n gegen Unendlich:
Für das Verhältnis der Flächeninhalte der blauen und roten Kreise zusammen
zum Quadrat gilt für n gegen Unendlich:
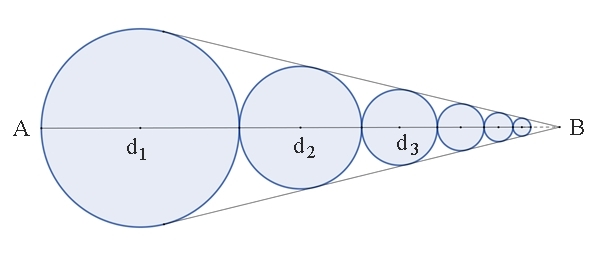
Kreiskette im goldenen Schnitt Beim goldenen Schnitt gelten folgende Bezeichnungen und
Beziehungen:
m = minor, M = Major
d1 = 1, d2 = σ, d3 = σ٠σ
= σ2, . . .
Für die
geometrische Reihe mit σ < 1 gilt:²
1 + σ + σ2 + σ3 + . . . = 1 / (1– σ) |AB| = 1 / (1 – σ) = 2
+ σ ≈
2,618
Für den Flächeninhalt der
Kreiskette mit Radius r1 = 1 gilt: 12π + σ2π + σ4π + σ6π + … = π (1 + σ² + (σ²)2 + (σ²)3 + …) = π τ
NR: Formel für geometrische Reihe anwenden
1 + σ² + (σ²)2 + (σ²)3 + … =
Folgerung:
Der Flächeninhalt der Kreiskette
ist das
τ-fache
des Flächeninhalts des Ausgangskreises.
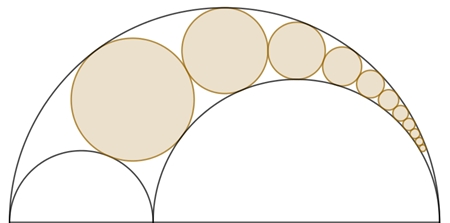
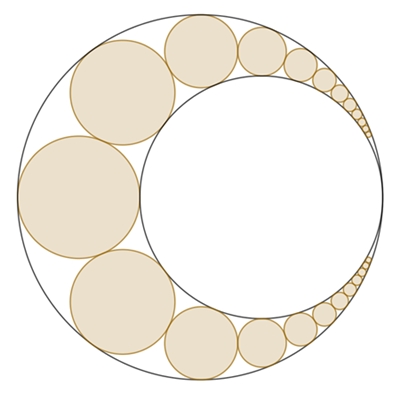
Pappos-Ketten
Pappos-Kette im Arbelos
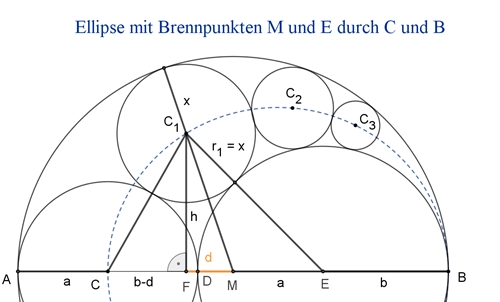
Ellipse mit Brennpunkten M und E durch die Mittelpunkte der Pappos-Kreise
Radius r um M: r = a + b, |FM| = d, |CF| = b – d
II (a + x)² = (b – d)² + h²
(Pythagoras im ΔCFC1)
III (b + x)² = (a + d)² + h²
(Pythagoras im ΔFEC1)
II – I = IV 2 x (2 a + b) – 2
a b – b² = b²
- 2 b d
II – II = V x (2 b – 2 a)
– a² + b² = a² – b² + 2 (a + b) d
IV٠(a + b) + V٠b
liefert
4 x (a² + a b + b²) – 3 a b (a + b) = a b (a + b)
Allgemein gilt für den Radius rn des n-ten Kreises mit
Mittelpunkt Cn:
Flächeninhalt der Pappos-Kette
Für a = 1 und b = 2 ergibt sich als Flächeninhalt:
Der Umfangshalbkreis hat den Flächeninhalt
½ (a+b)² π ≈
14,1372
Der Flächenanteil der
Pappos-Kette beträgt 4,4731
/ 14,1372٠100%
≈ 31,64
%
Für b = 2 und a = 1 ergibt sich als
Flächeninhalt:
2٠4,4731 + 1²π
≈ 12,0878
Der Umfangskreis hat den Flächeninhalt 28,2743
Der Flächenanteil der
Pappos-Kette beträgt 42,75%
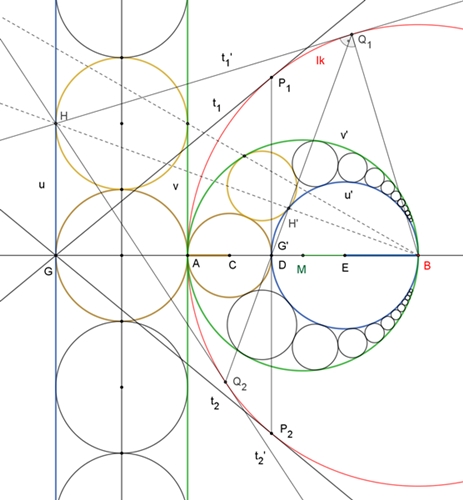
Konstruktion der Pappos-Kette mit Hilfe der Inversion am Kreis
Senkrecht übereinander liegende, sich
berührende kongruente Kreise werden an dem Inversionkreis Ik mit Mittelpunkt
B gespiegelt, wobei gilt mit R = |AB|:
|BP‘| = R²
/ |BP|
Der Spiegelpunkt H‘ liegt:
Ford-Kreise
Die Ford-Kreise
sind nach dem amerikanischen Mathematiker
Lester Randolph Ford senior (1886
– 1967) benannt.
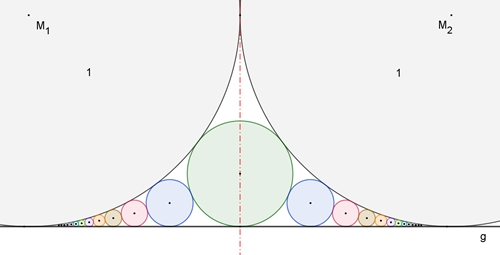
a) Einfache Ford-Kreise
Gegeben seien 2
sich berührende Kreise mit dem Radius 1 und eine Gerade g (Tangente), die
die beiden Kreise berührt. Die Kreise, die die Ausgangskreise, die Gerade
und die angrenzenden Kreise berühren, sind die einfachen Ford-Kreise.
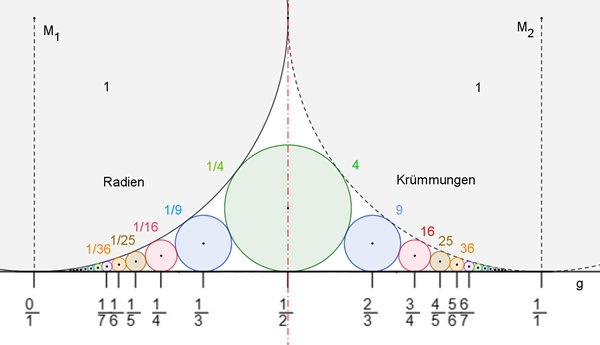
Diese Ford-Kreise
mit den Radien r und den Krümmungen
κ
= 1/r haben besondere Eigenschaften: Die Krümmungen nehmen quadratisch zu, wobei die Radien quadratisch abnehmen.
Ordnet man
der senkrechten Projektion von M1 auf die Gerade g als
Zahlenstrahl die Zahl 0 und von M2 auf die Gerade g die Zahl 1
zu, so bilden die senkrechten Projektionen der Mittelpunkte der Ford-Kreise
auf die Gerade g (Berührpunkte) die wie folgt dargestellten Brüche auf dem
Zahlenstrahl:
Auf der linken
Seite entspricht der Wurzel aus dem Radius der zugehörige Bruch. Auf der
rechten Seite sind es die entsprechend spiegelbildlichen Brüche.
Das ist ungefähr
10,2% der Fläche des Ausgangskreises.
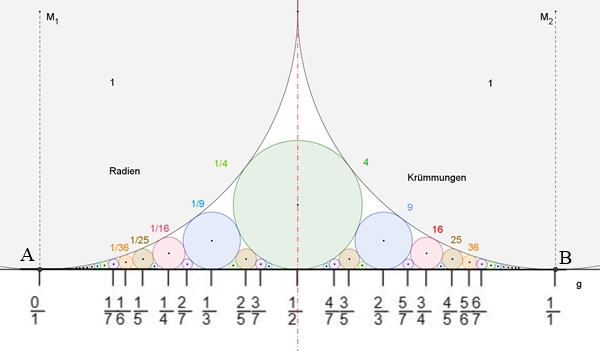
b) Komplexere Ford-Kreise
Es kommen noch
zusätzliche sich berührende Kreise hinzu, die auch die einfachen Ford-Kreise
und die Gerade berühren.
Die den
Ford-Kreisen zugeordneten Brüche stellen sog. Farey-Folgen dar.
Farey-Folgen
zugeordnete Farbkreise
A – grün – B
A – blau – grün – blau – B
A – rosa – blau – grün – blau – rosa –
B
A – braun – rosa – blau – braun – grün
– braun – blau – rosa – braun – B
Bemerkung:
Eine Farey-Folge ist eine geordnete Menge von
vollständig gekürzten Brüchen zwischen 0 und 1, deren jeweiliger Nenner
größer oder gleich dem Zähler ist.
|