Ineinander geschachtelte reguläre (regelmäßige) Vielecke

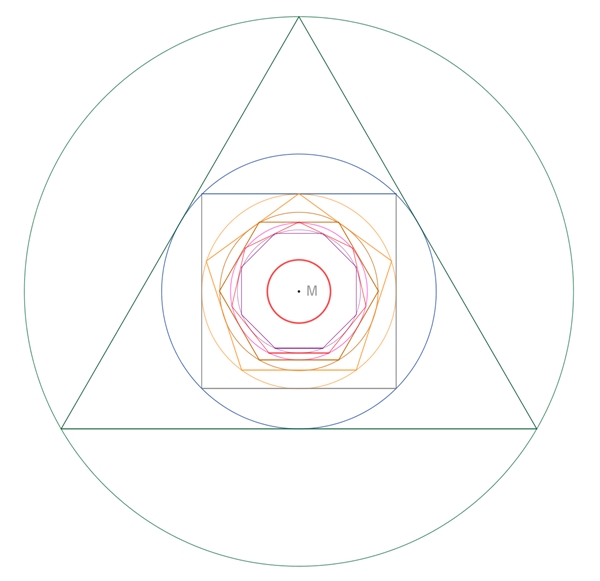
Reguläre Vielecke werden wie dargestellt ineinander geschachtelt. Dabei wird der Inkreis des vorhergehenden regulären Vielecks zum Umkreis des nachfolgenden regulären Vielecks. In- und Umkreise sind konzentrische Kreise mit gemeinsamen Mittelpunkt M.

Verhältnis Inkreis zu Umkreis im regulären n-Eck:

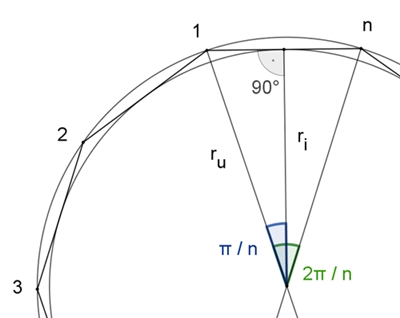
Im regulären n-Eck mit dem

Inkreisradius ri_n und dem Umkreisradius ru_n gilt:

ri_n / ru_n  =  cos(π/n) 

ri_n  =  cos(π/n) ٠ ru_n 

Aus dem Inkreis des regulären n-Ecks wird der Umkreis des regulären (n+1)-Ecks und so werden der Reihe nach gleichseitiges Dreieck, Quadrat, reguläres Fünfeck, reguläres Sechseck usw. ineinander geschachtelt.

Der Umkreisradius ru₃ des gleichseitigen Dreiecks habe den Wert 1.

Der Inkreisradius ri₃ ist gleich dem Umkreisradius ru₄ und hat dann den Wert
ru₄ = ri₃ = cos(π/3) = 0,5

Der Inkreisradius ri₄ ist gleich dem Umkreisradius ru₅ und hat dann den Wert
ru₅ = ri₄ = cos(π/3) ٠ cos(π/4) = √2/4 ≈ 0,3536
…

Der Inkreisradius ri_n ist gleich dem Umkreisradius ru_n+1 und hat dann den Wert
ru_n+1 = ri_n = cos(π/3) ٠ cos(π/4) ٠ cos(π/5)٠ … ٠ cos(π/n)

Für n → ∞ ergibt sich der Grenzwert ru_∞ = ri_∞ ≈  0,1150043965.

In obiger Figur ist der Grenzkreis als kleiner roter Kreis dargestellt.

Zurück
Zurück zur Startseite