|
Julia- und Mandelbrot-Mengen
Der französische Mathematiker Gaston
Maurice Julia führte 1918 zusammen mit Pierre Fatou die nach ihm benannte
Julia-Menge ein. Sie spielen
eine wichtige Rolle in der Theorie der dynamischen Systeme.
Die Rekursion
zn+1
=
f(zn
+ c) mit n ϵ ℕ0 und
komplexen Zahlen z mit Startwert z0
und der Konstante c kann beschränkt oder unbeschränkt sein und bildet damit
die Gefangenenmenge oder die Fluchtmenge. Die
Julia-Menge zur gegebenen
komplexen Konstante c ist der Rand der Gefangenenmenge. Die Julia-Menge lässt sich anschaulich in der komplexen Zahlenebene darstellen.
Die komplexe Zahl z = x + y٠i
wird als Punkt P(x | y) im Koordinatensystem mit der reellen Achse
als x-Achse und der imaginären Achse als y-Achse dargestellt.
Dabei werden die komplexen Zahlen, deren Rekursion beschränkt
ist, als Punkte schwarz dargestellt. Die komplexen Zahlen, deren Rekursion
gleich schnell über eine Schranke führt, werden als Punkte mit gleicher
Farbe dargestellt.
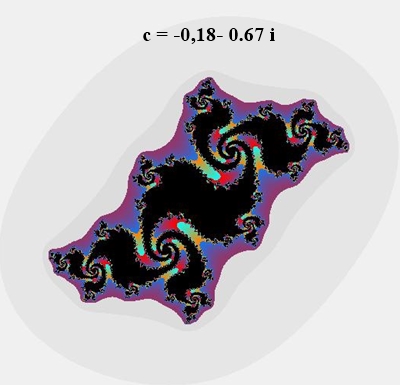
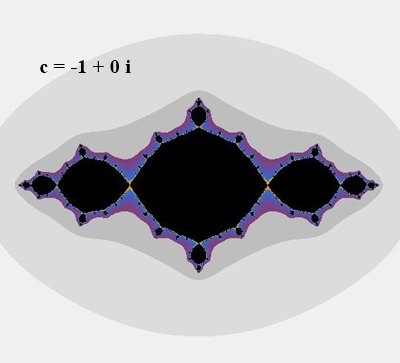
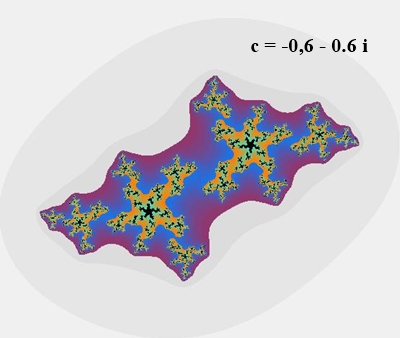
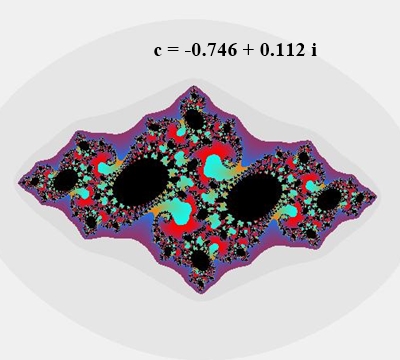
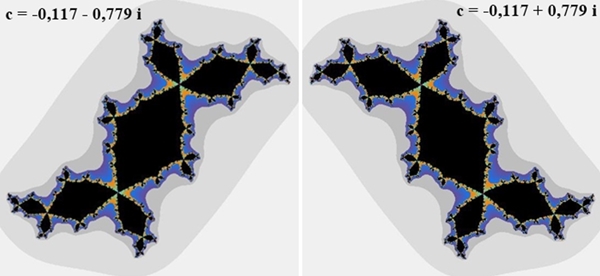
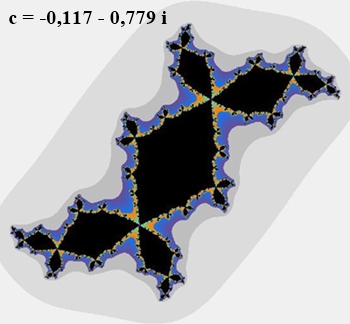
Zusammenhängende Julia-Mengen
(jeweils Rand des schwarzen Bereichs):
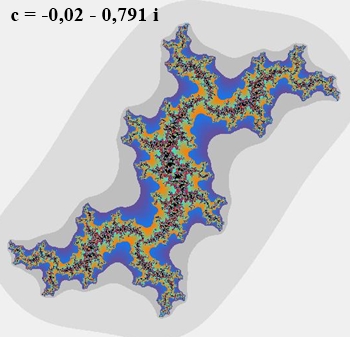
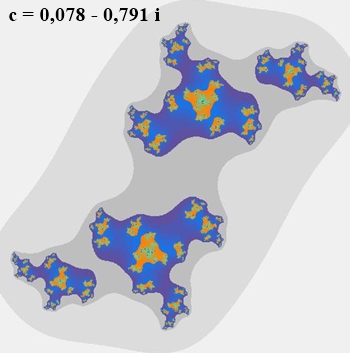
Nicht zusammenhängende Julia-Mengen:
Bei Verzicht auf Farbgebung kommt die Julia-Menge besser zur Geltung.
Eigenschaften
der Julia-Menge:
Bilder von Julia-Mengen sind punktsymmetrisch zum Ursprung
Bilder von Julia-Mengen mit konjugiert komplexen c, d.h. c = a + bi und c =
a – bi, sind achsensymmetrisch.
Die
Mandelbrot-Menge
Der französische Mathematiker Benoît
B. Mandelbrot begann 1979 mit dem Studium der Julia-Mengen. Dabei
entdeckte er die nach ihm benannte Mandelbrot-Menge.
Die Mandelbrot-Menge ist die
Menge der komplexen Zahlen c, für welche die durch die Iteration
Beispiele für Iterationen
Startwert der Rekursion: c = 0,1 – 0,4 i
0
0.1000 -0.4000
1
-0.0500 -0.4800
2
-0.1279 -0.3520
3
-0.0075 -0.3100 . . . 28
-0.0373 -0.3723 29
-0.0372 -0.3723 30
-0.0372 -0.3723
Die Iterationen führen zum Grenzwert –
0,0372 – 0,3723 i
Startwert der Rekursion: c = 0,078 – 0,791 i
0
0.0780 -0.7910
1
-0.5416 -0.9144
2
-0.4648
0.1995
3
0.2542 -0.9764
4
-0.8108
-1.2875
5
-0.9223 1.2967
6
-0.7528 -3.1830
7
-9.4867 4.0011
8
74.0656 -76.7060
9
-398.0106 -11363.3446
Die Iterationen führen über eine vorgegebene Grenze
Startwert der Rekursion: c = – 0,117 –
0,779 i
0
-0.1170 -0.7790
1
-0.7102 -0.5967
2
0.0312 0.0685
3
-0.1207 -0.7747 . . . 26 0.0273
0.0574 27
-0.1196 -0.7759 28
-0.7047 -0.5935 29 0.0273
0.0574
30
-0.1196 -0.7759 31
-0.7047 -0.5935
Die Iterationen bleiben beschränkt mit dreifacher Periode.
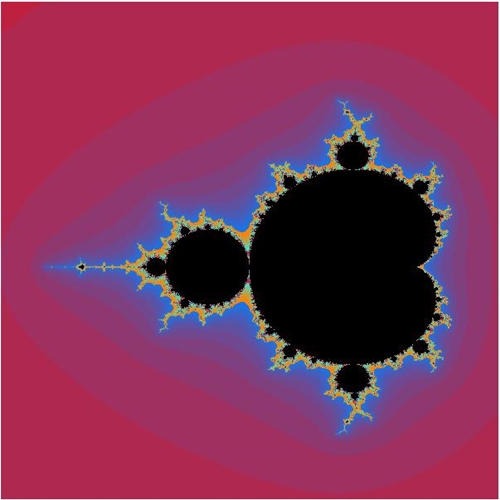
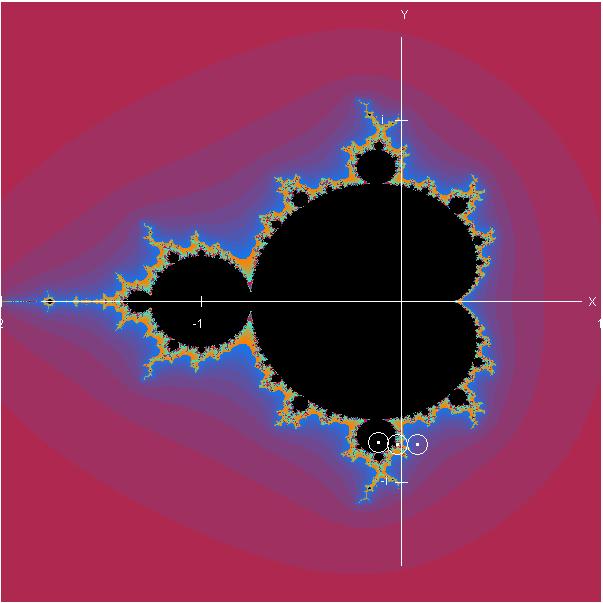
Geometrisch lässt sich die Mandelbrot-Menge (auch wegen der Form
Apfelmännchen genannt) als Punkte in der komplexen Zahlenebene anschaulich
darstellen. Die Mandelbrot-Menge wird dabei meist mit schwarzer Farbe
dargestellt, während gleichfarbige Punkte in ihrer Umgebung bedeuten, dass
die Rekursion gleich schnell über eine vorgegebene Schranke führt.
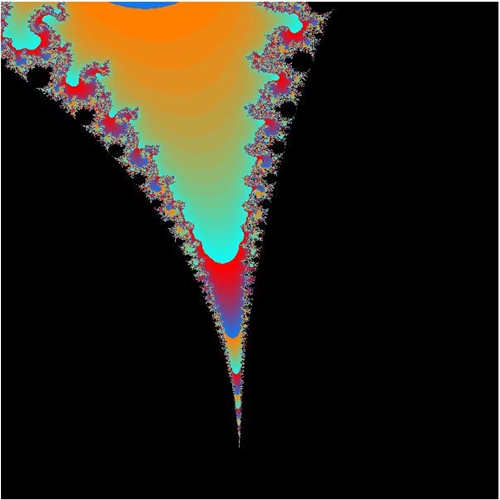
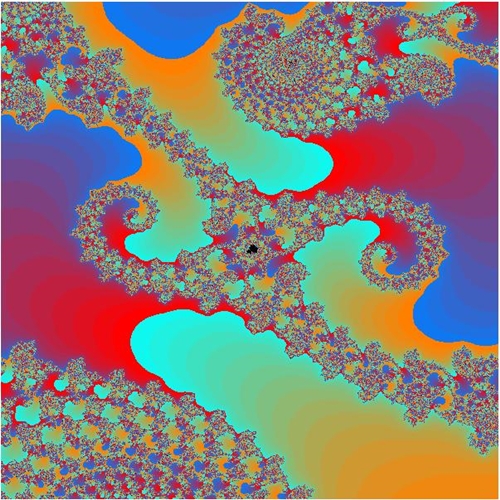
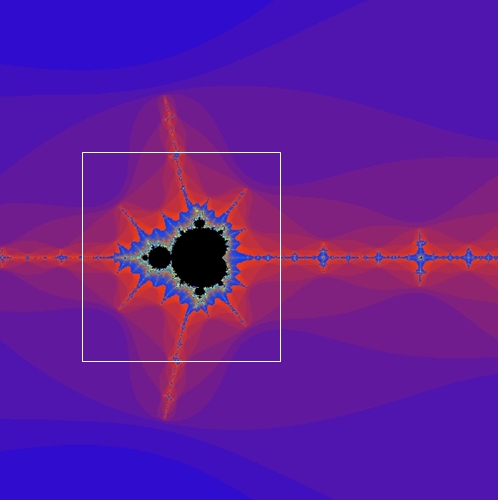
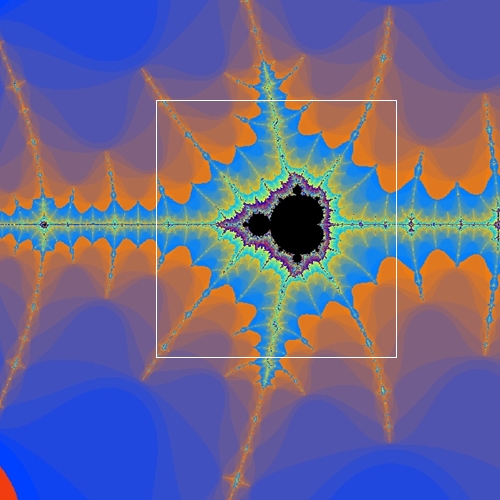
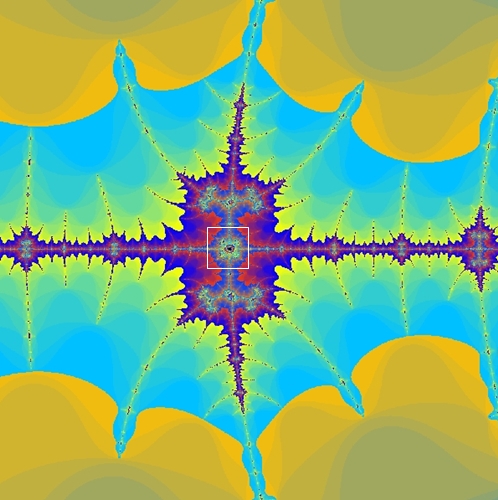
Zoom in die Mandelbrot-Menge mit dem
Zentrum
- 0,7454 + 0,113 i
Auf der Suche nach Apfelmännchen:
Eigenschaften der
Mandelbrot-Menge:
Die Mandelbrotmenge ist achsensymmetrisch zur x-Achse (reellen Achse)
Die Mandelbrot-Menge ist abgeschlossen und liegt innerhalb eines Kreises mit
Radius 2. Sie ist auch zusammenhängend, d.h. sie bildet keine Inseln.
An den fraktalähnlichen Strukturen am Rand der Mandelbrot-Menge bilden sich
in Verkleinerung immer wieder Mandelbrot-Mengen Der Rand der Mandelbrot-Menge ist unendlich lang. Sie hat aber einen bestimmten Flächeninhalt, ungefähr 1,507 F.E.
Es besteht ein enger Zusammenhang zwischen Mandelbrot-Menge und
Feigenbaum-Diagramm
und damit auch mit dem
deterministischen Chaos. Die Mandelbrotmenge ist ein fraktalähnliches Gebilde.
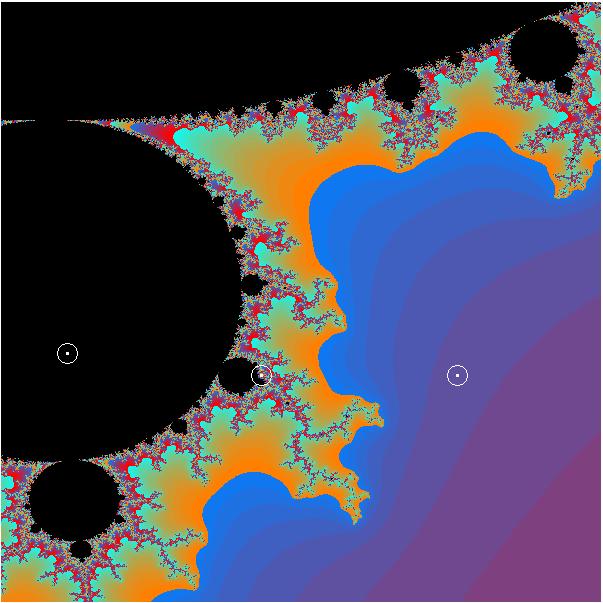
Zusammenhang zwischen Julia- und Mandelbrot-Menge:
Julia-Mengen für die gekennzeichneten Punkte c der schwarz dargestellten
Mandelbrot-Menge mit farbiger Umgebung:
Wird die Konstante c der Julia-Menge als komplexe Zahl aus der
Mandelbrot-Menge gewählt, so ist die Julia-Menge zusammenhängend,
andernfalls nicht zusammenhängend.
Beide Mengen sind fraktalähnliche Gebilde und in Näherung selbstähnlich.
|