Logistische Gleichung, Feigenbaum-Diagramm, Lorenz-Attraktor und deterministisches Chaos

x_n+1  =  r ٠ x_n ٠ (1 – x_n) 

wurde von dem belgischen Mathematiker Pierre-François Verhulst zur Beschreibung der Populationsentwicklung von Tierarten in einem bestimmten Lebensraum entwickelt.
Die Gleichung stellt eine Rekursion dar.

Wenn man die beiden Seiten jeweils als Funktionen mit den Gleichungen

f(x) = x  und  g(x) = r ٠ x ٠ (1 – x)

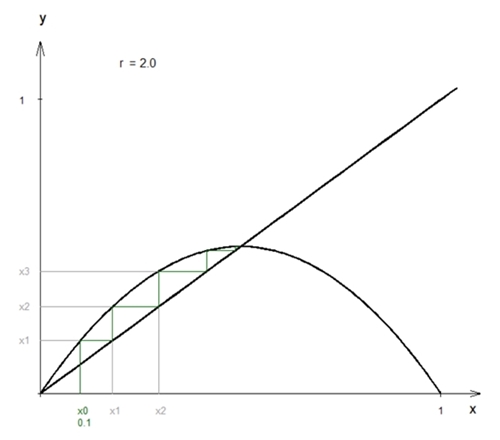
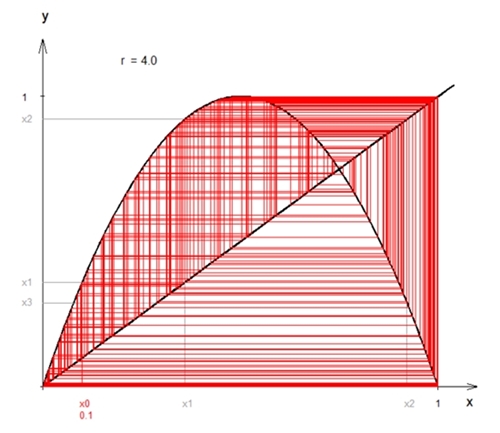
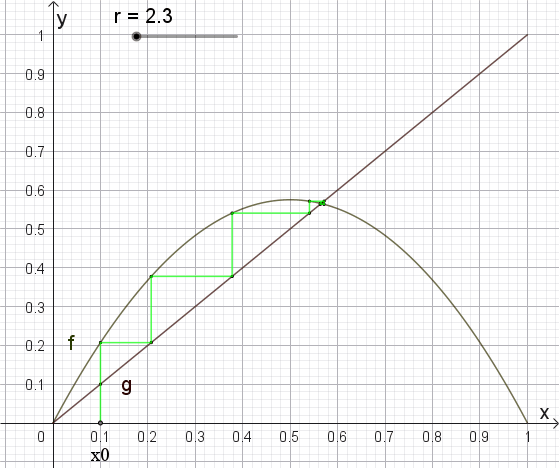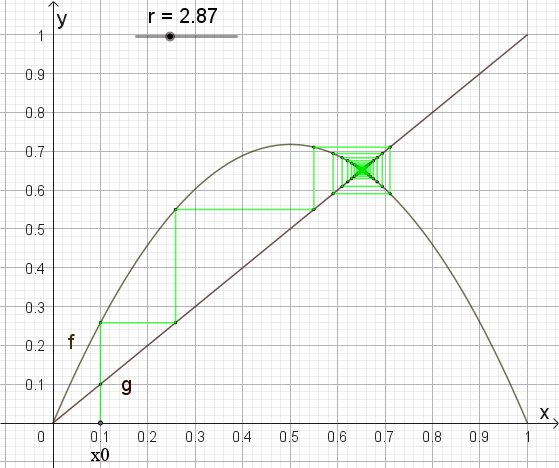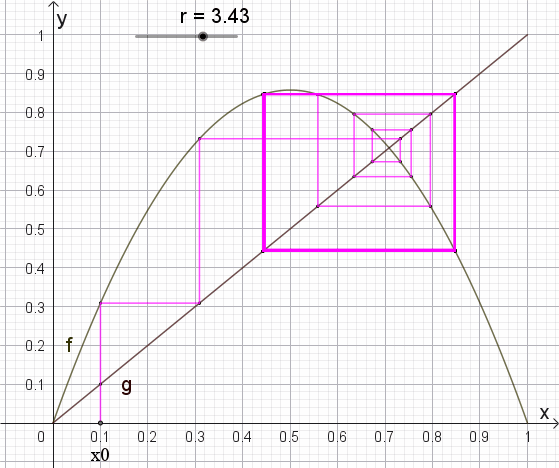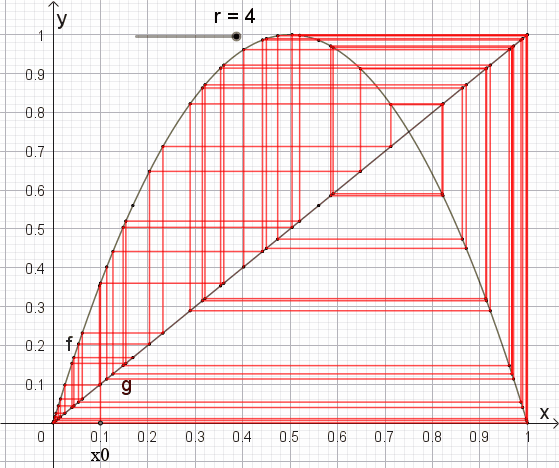
betrachtet, lassen sich die Rekursionen anschaulich z.B. mit dem Startwert x₀ = 0,1 folgendermaßen darstellen:

Dabei stellt die Funktion g eine nach unten geöffnete Parabel mit dem Scheitelpunkt S(r/4 | 0,5) dar.

Die Rekursionen liefern als Ergebnis

für  r = 2,0 die Zahl 0,5

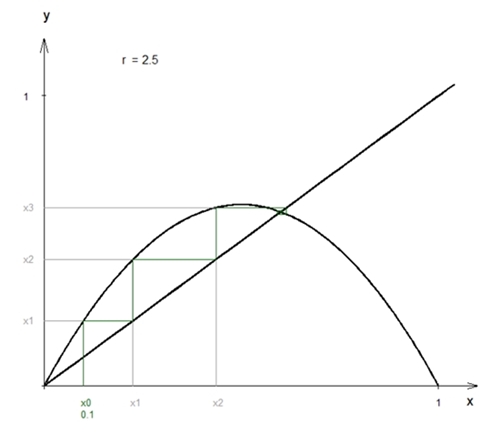
für  r = 2,5 die Zahl 0,6

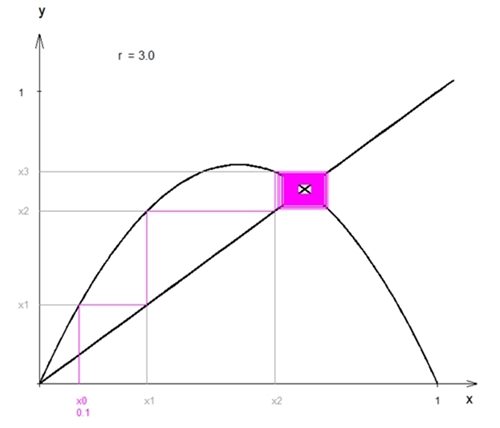
für  r = 3,0 die Zahl  0,667  (3D) (nach vielen Iterationen)

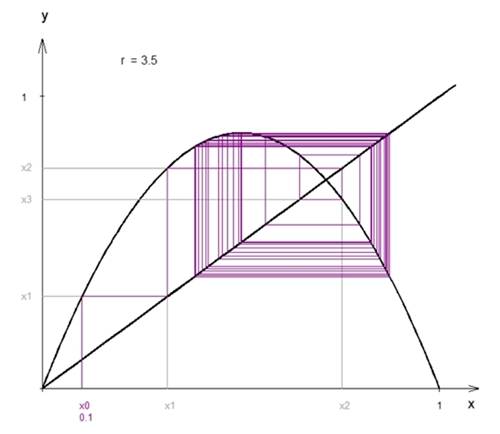
für  r = 3,5 die alternierende Zahlen  0,383  0,827  0,501  0,875

für  r = 4,0  zufällig verteilte Zahlen

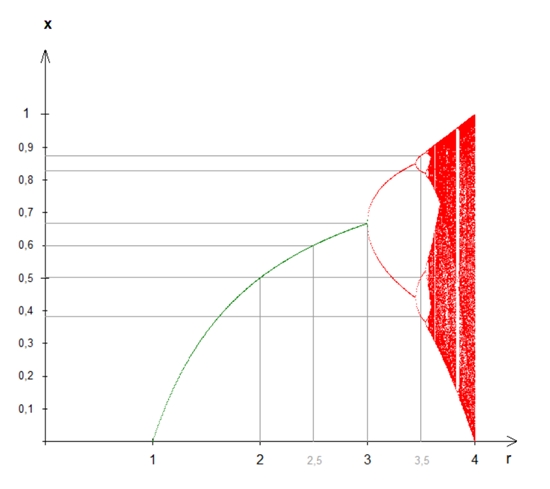
Feigenbaum-Diagramm

Dieses seltsame Verhalten hat der amerikanische Physiker und Chaosforscher Mitchell Jay Feigenbaum im sog. Feigenbaum-Diagramm 1975 bei Untersuchungen von Turbulenzen in Flüssigkeiten zusammengefasst.  

Die horizontale Achse gibt den Wert des Parameters r an und die vertikale Achse die Häufungspunkte für die Folge x_n (x-Achse).

Bei r₀ = 3 und x = 0,667 (3D) beginnt die erste Bifurkation (Aufspaltung) in zwei Zweige (Periodenverdoppelung) und liefert dann zwei verschiedene Ergebnisse bei der Rekursion der logistischen Gleichung.
Bei r₁ = 1 +   = 3,449 (3D) beginnt die Aufspaltung in 4 Zweige, für r = 3,5 ergeben sich dann bei der Rekursion die 4 verschiedenen Ergebnisse 0,383 | 0,501 | 0,827 | 0,875 (3D).

Bei r₂  = 3,544 (3D) beginnt die Aufspaltung in 8 Zweige
Bei r₃  = 3,564 (3D) beginnt die Aufspaltung in 16 Zweige

Ab   = 3,5699 (4D) wird das Verhalten der Rekursion chaotisch.

Man bezeichnet es als deterministisches Chaos.

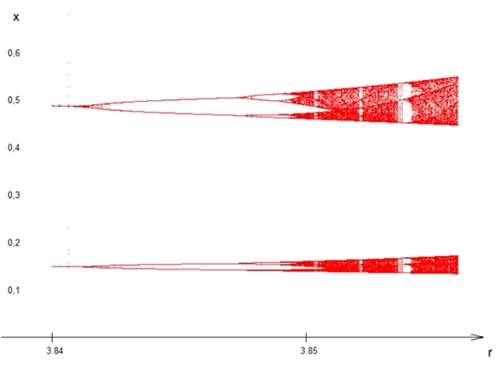
Um r = 3,84 fällt ein weißer Bereich auf.

In diesem Bereich scheint sich tatsächlich wieder eine Ordnung zu ergeben. Bei einer Ausschnittsvergrößerung des Bereiches 3,84 bis 3,856 ist wieder ein Feigenbaum-Diagramm zu erkennen:

Das Feigenbaum-Diagramm zeigt damit Eigenschaften eines Fraktals.

Feigenbaum entdeckte zwei Konstanten, die nach ihm benannt wurden. Diese Konstanten treten bei nichtlinearen Systemen auf, die in Abhängigkeit von einem Parameter reguläres oder chaotisches Verhalten zeigen.

Das Verhältnis der Längen aufeinander folgender Periodenintervalle unterschiedlicher Periode strebt dabei gegen die Feigenbaum-Konstante δ.

Die Feigenbaum-Konstante δ berechnet sich folgendermaßen, wenn man die i-te Bifurkationstelle als r_i bezeichnet:

δ =    Anfangsverhältnis: 

Der Abstand d_i  zwischen den einzelnen Gabelungsspitzen bei der i-ten Bifurkation ergibt die Konstante α als Grenzwert des Verhältnisses von d_n zu d_n+1:

Für r₂ = 3,54409 ergeben sich dann bei der Rekursion die 4 verschiedenen Ergebnisse 0,3633 | 0,5236 | 0,8198 | 0,8840 (4D).

Anfangsverhältnis:

d₁  = 0,8499 – 0,4400;  d₂ = 0,5236  –  0,3633

Lorenz-Attraktor

Edward Norton Lorenz arbeitete 1963 mit Hilfe eines kleinen Computers und eines System von 12 Gleichungen, die als Variablen Temperatur, Luftdruck, Windrichtung u.a. enthielten, an der Lösung eines dynamischen Wettermodells. Doch als er die Gleichungen ein weiteres Mal durchrechnen ließ, stellte er fest, dass die sechsstellige Dezimalzahl als Startwert auf drei Dezimalstellen gerundet worden war. Diese minimale Veränderung führte zu einem völlig anderen Ergebnis der Wettervorhersage.

Lorenz hat seine zunächst 12 Gleichungen auf 3 Gleichungen reduziert mit der Rekursionsdarstellung:

x_n+1 = x_n – a٠x_n٠dt + a٠y_n٠dt

y_n+1 = y_n + b٠x_n٠dt – y_n٠dt – x_n٠z_n٠dt

z_n+1 = z_n – c٠z_n٠dt + x_n٠y_n٠dt

Für die Konstanten wählte Lorenz a = 10;  b = 28;  c = 8/3
(a = Prandtl-Zahl, b = Raleigh-Zahl)

Ihre Iteration führt zu einem Attraktor, der nach ihm  als Lorenz-Attraktor benannt wird. Dieser „seltsame Attraktor“ beschreibt das Verhalten eines chaotischen dynamischen Systems. (siehe Lorenz-Gleichungen)

 Der Lorenz-Attraktor hat auch die Eigenschaften eines Fraktals.

Deterministisches Chaos

Die Arbeiten von Edward Norton Lorenz und die sensitive Abhängigkeit von den Anfangsbedingungen wurde als Schmetterlingseffekt bekannt und stellt den Beginn der Chaosforschung dar. Sie wurde von Mitchel Feigenbaum 1975 und von Benoît B. Mandelbrot 1979 wesentlich weiterentwickelt.

Die Chaostheorie beschäftigt sich mit Ordnungen in nichtlinearen dynamischen Systemen, die eine nicht vorhersehbare zeitliche Entwicklung besitzen. Da die Ausgangsgleichungen festgelegt (deterministisch sind, spricht man von deterministischem Chaos.

Ein einfaches Modell für das deterministische Chaos liefert die logistische Gleichung und deren Veranschaulichung, die zum Feigenbaum-Diagramm führt.

Wesentliche Erkenntnisse der Chaostheorie:

Eine längerfristige Vorhersage über das Verhalten mancher Systeme ist grundsätzlich nicht möglich.

Sehr kleine Änderungen bei bestimmten Systembedingungen können sehr große Wirkungen hervorbringen.

Die linearen Näherungen in den Wissenschaften haben nur eine begrenzte Aussage und manchmal bildet nichtlineares Verhalten die Realität besser ab.

Komplexe Systeme können sich ganz einfach verhalten (Ordnung im Chaos) während einfache Systeme chaotisches Verhalten zeigen.

Es gibt in den verschiedenen Wissenschaftsbereichen über die Chaostheorie strukturelle Ähnlichkeiten.  

Beispiele für Deterministisches Chaos:

Wettervorhersagen

Herzkammerflimmern und Herzinfarkt

Turbulenzen

Verkehrschaos durch viele Verkehrsteilnehmer mit ihren Bewegungsmöglichkeiten (Freiheitsgraden)

Börsenkurse und Konjunkturentwicklung

Schwingungen eines Doppelpendels; Magnetpendel

Die Bilder wurden mit Hilfe der Programmiersprache Python39 erzeugt.