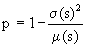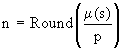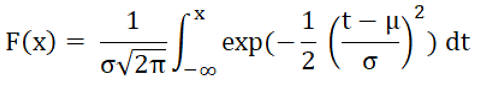Wie zufällig sind die Primzahlen verteilt?

Um zu testen, wie zufällig Primzahlen in Zahlenbereichen verteilt sind, bietet sich folgendes Vorgehen an.

Es werden gleich lange Reihen von natürlichen Zahlen in Zahlenbereichen gebildet. Dann wird jeweils pro Zeile die Anzahl der Primzahlen bestimmt. Schließlich wird die relative Häufigkeit der Anzahl der Primzahlen als Zufallsgröße X für eine vorgegebene Anzahl von Zeilen der Länge s rechnerisch ermittelt und graphisch als Histogramm dargestellt.

Der Erwartungswert von X sei μ(s), die Standardabweichung σ(s).

Es lässt sich nun eine Binomialverteilung auf Grund des Erwartungswertes μ(s) und der Standardabweichung σ(s) zuordnen:

μ(s)  =  n p     und   [σ(s)] ²  =   n p (1–p).

Daraus folgt für p und n der Binomialverteilung:

    und   

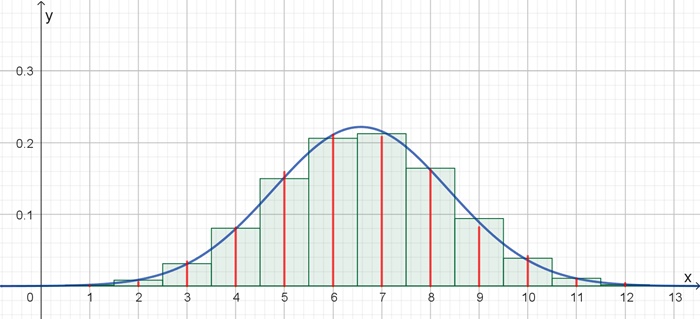
Da n eine natürliche Zahl ist, muss gerundet werden.

Der relativen Häufigkeit der Anzahl der Primzahlen wird auch die Verteilungsfunktion F(x) der Normalverteilung zugeordnet mit dem Erwartungswert µ = µ(s) und der Standardabweichung σ = σ(s), exp( ) = e^{( )}.

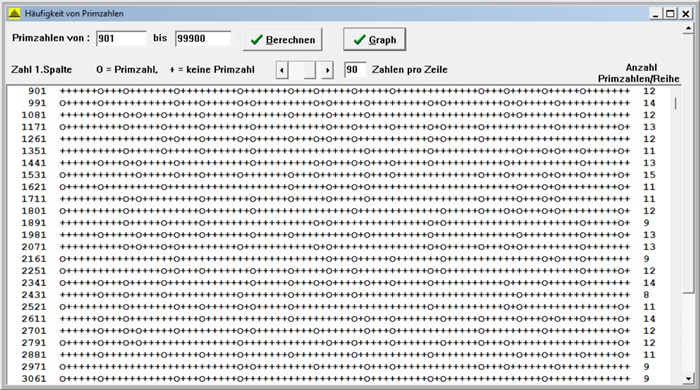
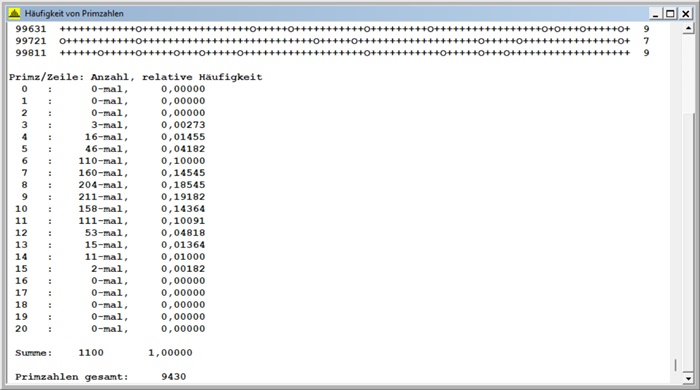
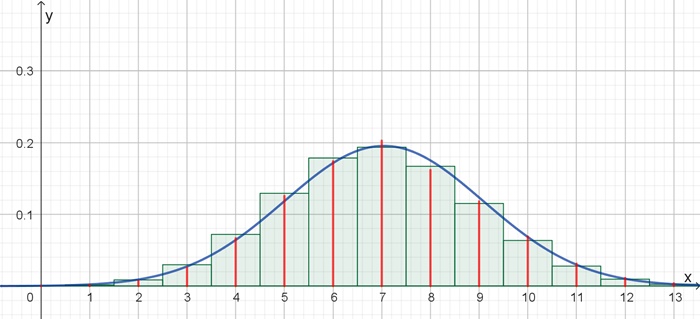
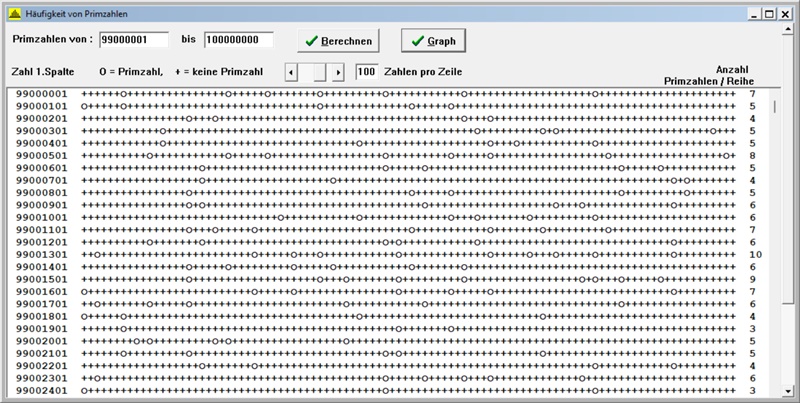
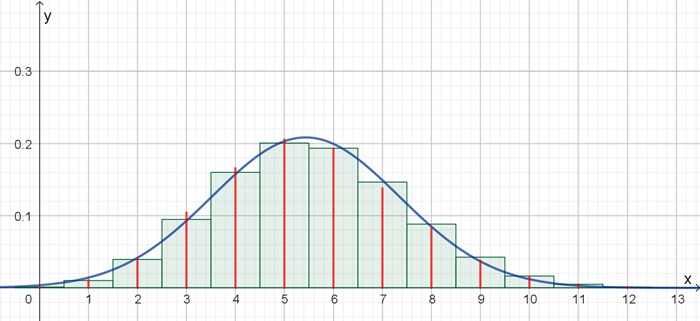
Folgende Beispiele zeigen die rechnerische und graphische Umsetzung mit einem Delphi-Programm und mit Geogebra:

Die relative Häufigkeit der Primzahlen wird mit roter Farbe, die Binomialverteilung mit grüner Farbe und die Verteilungsfunktion der Normalverteilung mit blauer Farbe dargestellt, o bedeutet Primzahl, + keine Primzahl.

A) Primzahlen zwischen 901 und  99 900, Zeilenlänge s = 69

Berechnung des Erwartungswertes E(X) = µ(s) der Verteilung der Anzahl der Primzahlen mit Zeilenbreite s = 69:

E(X) = µ(s) = 1٠0,0007 + 2٠0,00557 + 3٠0,03415 + 4٠0,08153 + 5٠0,15889 + 6٠0,21115 + 7٠0,20767 + 8٠0,16237 + 9٠0,08223 + 10٠0,04181 + 11٠0,00976 + 12٠0,00418
µ(s) = 6,5701

Berechnung der zugehörigen Standardabweichung σ(s) mit der Formel

σ²(s) = 1²٠0,0007 + 2²٠0,00557 + 3²٠0,03415 + 4²٠0,08153 + 5²٠0,15889 + 6²٠0,21115 + 7²٠0,20767 + 8²٠0,16237 + 9²٠0,08223 + 10²٠0,04181 + 11²٠0,00976 + 12²٠0,00418 - 6,5701²
σ(s) = 1,7984

Histogramm Erwartungswert: µ = µ(s) = 6,570, 

Histogramm Standardabweichung:  σ = σ(s) = 1,798

Zugeordnete Binomialverteilung: B(13; 0,5077) mit
Erwartungswert 6,600 und Standardabweichung 1,803

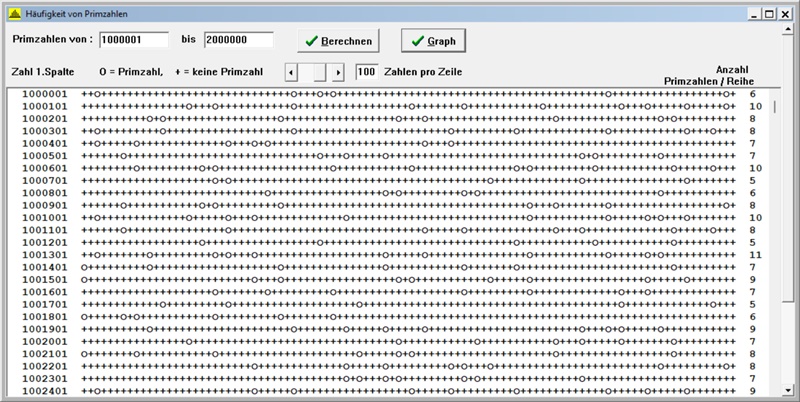
B) Primzahlen zwischen 1 000 001 und 2 000 000, Zeilenlänge s = 100

Histogramm Erwartungswert: µ = µ(s) = 7,044, 

Histogramm Standardabweichung:  σ = σ(s) = 2,041

Zugeordnete Binomialverteilung: B(17; 0,4083) mit
Erwartungswert 6,942 und Standardabweichung 2,027

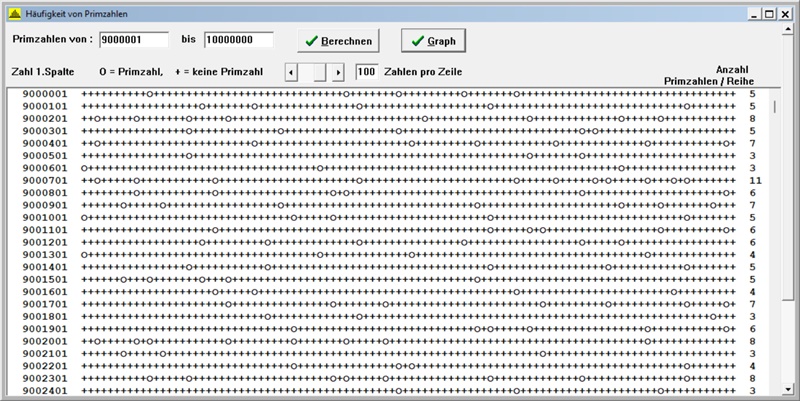
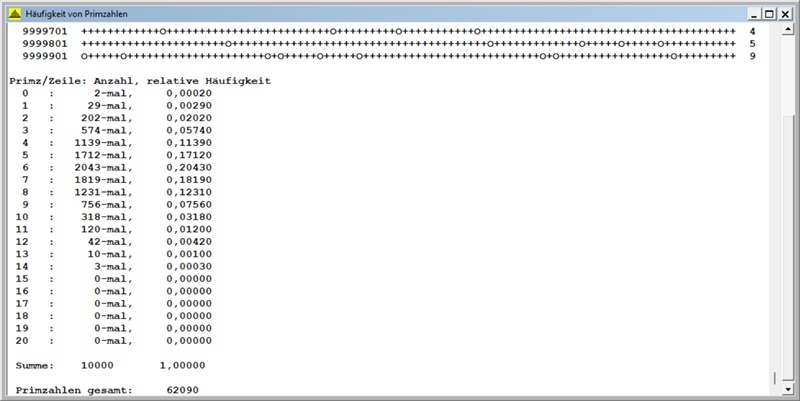
C) Primzahlen zwischen 9 000 001 und 10 000 000, Zeilenlänge s = 100

Histogramm Erwartungswert: µ = µ(s) = 6,209, 

Histogramm Standardabweichung:  σ = σ(s) = 1,971

Zugeordnete Binomialverteilung: B(17; 0,3742) mit
Erwartungswert 6,362 und Standardabweichung 1,995

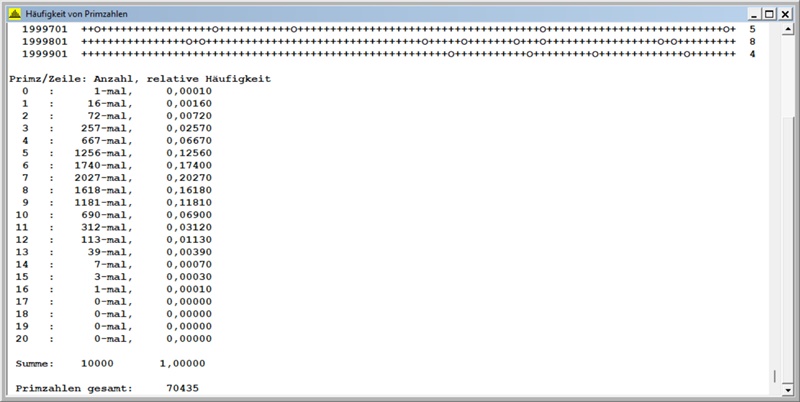
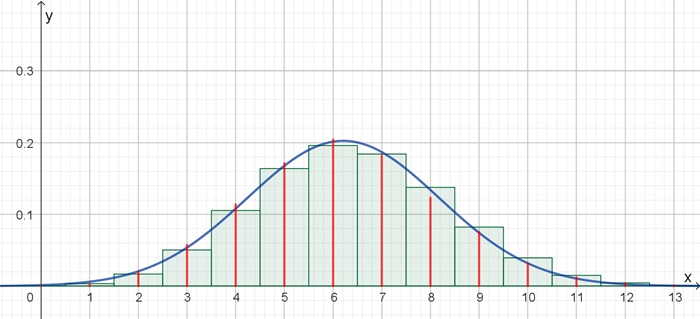
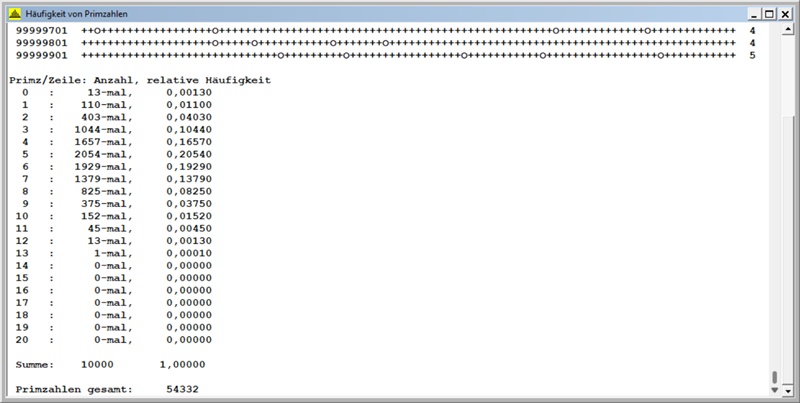
D) Primzahlen zwischen 99 000 001 und 100 000 000, Zeilenlänge s = 100

Histogramm Erwartungswert: µ = µ(s) = 5,433, 

Histogramm Standardabweichung:  σ = σ(s) = 1,915

Zugeordnete Binomialverteilung: B(17; 0,325) mit
Erwartungswert 5,530 und Standardabweichung 1,932

Beim Vergleich von B, C und D bestätigt sich die abnehmende Dichte bei größer werdenden Primzahlen. Der Erwartungswert sinkt von 7,044 auf 6,209.

Die Binomialverteilung und die Verteilungsfunktion der Normalverteilung stellen eine Zufallsverteilung dar. Die relativ gute Übereinstimmung der Verteilungen legen den Schluss nahe, dass die Verteilung der Primzahlen in Zahlenbereichen mit gegebener Intervallbreite in Näherung binomial- bzw. normalverteilt erfolgt.