Fadengrafiken mit Primzahlen

1. Fall:

bⁿ mod p mit der Basis b und der Primzahl p mit n = 1, 2, 3 … p – 1
ist Ausgangspunkt interessanter Fadengrafiken.

Mit mod (Modulo) wird der Rest einer ganzzahligen Division bezeichnet,
z.B.  11 mod 3 = 2,  18 mod 5 = 3,  16 mod 4 = 0

6ⁿ mod 11, n = 1, 2, … 10
liefert 10 verschiedene Zahlen kleiner als 11:  [6, 3, 7, 9, 10, 5, 8, 4, 2, 1]

3 mod 11, n = 1, 2, … 10
liefert jedoch nur 5 verschiedene Zahlen kleiner als 11:  [3, 9, 5, 4, 1, 3, 9, 5, 4, 1]

Man sagt: 6 ist Primitivwurzel von 11, jedoch nicht 3.

bⁿ mod p mit n = 1, 2, 3 … p – 1

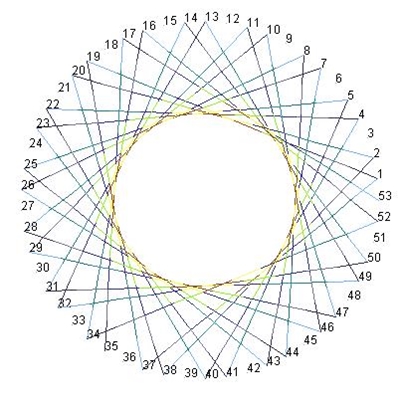
Veranschaulichung durch Plazierung der Punkte auf dem Rand eines Kreises mit Radius r  in einem xy-Koordinatensystem nach folgender Vorschrift:

                                          x = r٠cos(bⁿ mod p٠2π/n);  y = r٠sin(bⁿ mod p٠2π/n)

Die im günstigsten Fall p – 1 verschiedenen Punkte werden  dann für n = 1, 2, 3, …, p – 1 der Reihe nach mit einer geraden Linie verbunden. Dabei entstehen je nach Basis b und Primzahl p unterschiedliche Muster. Zur besseren Darstellung werden die Linien vom jeweiligen Startpunkt zum Zielpunkt im gleichen Verhältnis unterschiedlich gefärbt.

Beispiele:

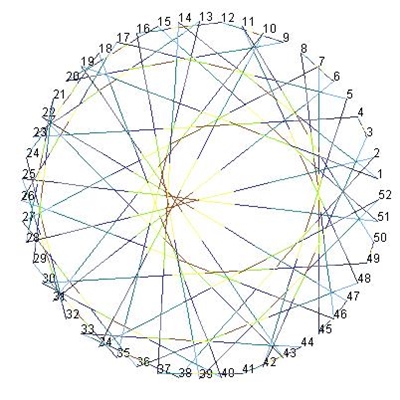
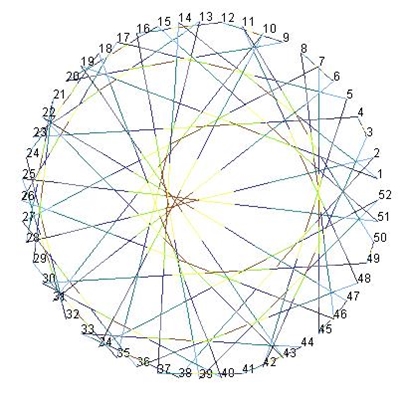
                     19ⁿ mod 569                                           115ⁿ mod 569                                           240ⁿ mod 991

                   51ⁿ mod 1009                                              47ⁿ mod 1049                                           60ⁿ mod 1427

Der kanadische Mathematiker Simon Plouffe (geb. 11.6.1956) hat sich eingehend mit Zahlentheorie beschäftigt und an der Veranschaulichung und Erfassung von Zusammenhängen bei  bⁿ mod p mit n = 1, 2, 3 … p – 1  gearbeitet.

Er hat folgendes Vorgehen entwickelt, um Muster und Spitzbögen in diesen Fadengrafiken zu erfassen:

P₁ = | (1 – b)٠[p/b] – b + p + 1 | = a,   [p/b] ist die ganze Zahl bei der Division von p durch b

P₀ = b – 1

Menge M(P₁) = {a, 2a, 3a, 4a, …}

Menge M(P₀) = {b–1, 2(b–1), 3(b–1), …}

Die Differenzen der Zahlen der beiden Mengen mit etwa 10 bis 20 Elementen bilden eine Menge von Zahlen, die wie auch P₁ und P₀ eine Aussage über Muster zulassen.

Beispiele: 

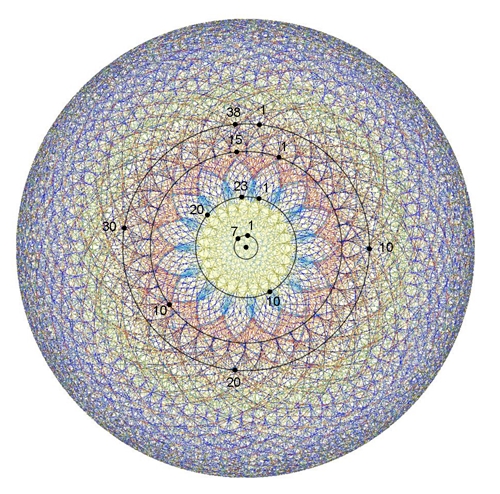
265ⁿ mod 1667  liefert die Werte P₀ = 264 und P₁ = 181

 
P₁ = | (1 – 265)٠[1667 /265] – 265 + 1667 + 1 | = | –181| = 181,  NR: [1667 /265] = 6

M(P₁) = {181, 362, 543, 724, 905, 1086, 1267, 1448, 1629, 1810, 1991, 2172, 2353, 2534, …}
M(P₀) = {264, 528, 792, 1056, 1320, 1584, 1848, 2112, 2376, 2640, …}.

Man bildet dann alle Differenzen zwischen jedem Paar von Elementen aus beiden Mengen und bildet eine neue Menge:
{15, 23, 30, 38, 53, 68, 83, 98, 113, 128, 136, 151, 166, …}.

NR: 543 – 528 = 15, 2376 – 2353 = 23, 792 – 724 = 68, 1086 – 1056 = 30, 1848 – 1810 = 38

Daraus entfernt man die Vielfachen einer Zahl. Die bereinigte Liste ist dann:
{15, 23, 38, 53, 68, 83, 98, 113, 128, 151, …}

Diese Menge stellt eine Liste von Punktgruppen dar. Man kann eine Gruppe von 15 oder 38 Spitzbögen in den beiden äußeren Kreisen zählen, während sich im inneren Kreis 23 Punktreihen mit Spitzen befinden. Auf dem Kreisrand sind 1666 nicht mehr unterscheidbare Punkte.

Eine 7teilige Punktgruppe um den Mittelpunkt wird jedoch nicht erfasst. 

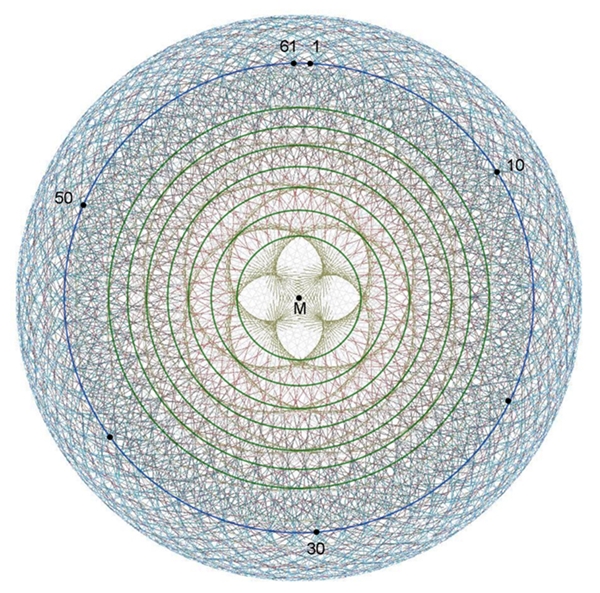
193ⁿ mod 1009  liefert die Werte P₀ = 192 und P₁ = 143.

P₁ = | (1 – 193)٠[1009 /193] – 193+ 1009 + 1 | = | –143| = 143,  NR: [1009 /193] = 5

M(P₁) = { 143, 286, 429, 572, 715, 858, 1001, 1144, 1287, 1430, 1573, 1716, 1859, 2002, 2145, 2288, …}

M(P₀) = { 192, 384, 576, 768, 960, 1152, 1344, 1536, 1728, 1920, 2112, 2304, …}

Differenzenmenge: {4, 8, 12, 16, 33, 37, 41, 45, 49, 53, 57, 61, 82, 86, 90, …}

NR: 576 – 572 = 4, 1152 – 1144 = 8, 1728 – 1716 = 12, 2880 – 2860 = 20, …

Die Vielfachen von 4 zeigen sich auch im Muster, gekennzeichnet durch grüne Kreise.
Die bereinigte Liste ohne Vielfache ist:
{4, 33, 37, 41, 45, 49, 53, 57, 61, 86,  …}

Auf dem blauen Kreis liegen 61 Schnittpunkte. Entsprechend sollen sich sich auch 33, 37, 41, … Schnittpunkte finden lassen.

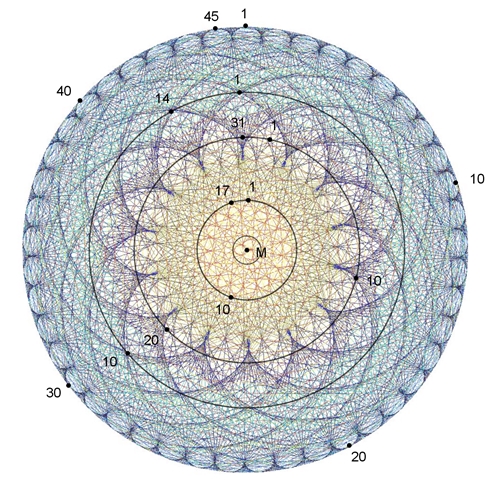
23ⁿ mod 1049  liefert die Werte P₀ = 22 und P₁ = 37.

P₁ = | (1 – 23)٠[1049 /23] – 23 + 1049 + 1 | = 37,  NR: [1049 /23] = 45

M(P₁) = { 37, 74, 111, 148, 185, 222, 259, 296, 333, 370, …}

M(P₀) = { 22, 44, 66, 88, 110, 132, 154, 176, 198, 220, …}

Differenzenmenge: {1, 2, 6, 7, 8, 9, 13, 14, 15, 16, 21, 23, 24, 28, 29, 30, 31, 35, 36, 39, …} 
Bereinigte Liste ohne Vielfache von Zahlen größer als 1: {1, 2, 7, 11, 13, 15, 23, 29, 31, 39, …}

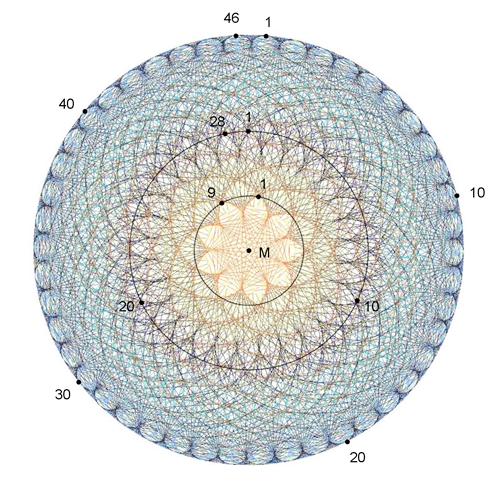
46ⁿ mod 1049  liefert die Werte P₀ = 45 und P₁ = 14.

P₁ = | (1 – 46)٠[1049 /46] – 46+ 1049 + 1 | = 14 ,  NR: [1049 /46] = 22

M(P₁) = { 14, 28, 42, 56, 70, 84, 98, 112, 126, 140, 154, 168, 182, 196, 210, 224, 238, 252, 266, 280, 294, 308, 322, 336, 350, 364, 378, 392, 406, 420, 434, 448, …}

M(P₀) = { 45, 90, 135, 180, 225, 270, 315, 360, 405, 450, …}

Differenzenmenge: {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 15, 16, 17, 18, 19, 20, …, 31, …}

Bereinigte Liste ohne Vielfache von Zahlen größer als 1:
{1, 2, 3, 5, 7, 11, 13, 17, 19, …, 31, …}

47ⁿ mod 1049  liefert die Werte P₀ = 46  und P₁ = 9 .

P₁ = | (1 – 47)٠[1049 /47] – 47 + 1049 + 1 | = 9,   NR: [1049 /47] = 22

M(P₁) = { 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, 108, 117, 126, 135, 144, 153, 162, 171, 180, 189, 198, 207, 216, 225, 234, 243, 252, 261, 270, …}

M(P₀) = { 46, 92, 138, 184, 230, 276, …}

Differenzenmenge: {1, 2, 3, 4, 5, 6, 7, 8, 10, 11, 12, 13, 14, 15, 16, 17, 19, 20, …}

Bereinigte Liste ohne Vielfache von Zahlen größer als 1:
{1, 2, 3, 5, 7, 11, 13, 17, 19, …, 28, …}

130ⁿ 𝑚𝑜𝑑 1009  liefert die Werte 𝑃₀ = 129  und 𝑃₁ = 23.

P₁ = | (1 – 130)٠[1009 /130] – 130 + 1009 + 1 | = 23,   NR: [1009 /130] = 7

M(P₁) = { 23, 46, 69, 92, 115, 138, 161, 184, 207, 230, 253, 276, 299, 322, 345, 368, 391, 414, 437, 460, 483, 506, 529, 552, 575, …}

M(P₀) = { 129, 258, 387, 516, 645, 774, 903, 1032, 1161, 1290, … }

Differenzenmenge: { 4, 5, 9, 10, 13, 14, 18, 19, 27, 28, 32, 33, 36, 37, … }

Bereinigte Liste:  { 4, 5, 9, 13, 14, 19, 33, 37, … }
 

Bei einer vergrößerten Darstellung des linken Bildes ist eine neue Struktur zu sehen.

Bemerkung:

Der Kreisrand besteht aus p – 1 Punkten. Daran schließt sich ein Muster aus P₀ = b – 1 Bögen an.

Je nach Farbgebung der Verbindungslinien werden verschiedene Strukturen stärker hervorgehoben. Bei den Strukturen spielen sowohl P₀ und P₁ als auch die bereinigten Differenzenengen eine Rolle.

Programm in TigerJython zur Darstellung der Fadengrafiken

# b^n_mod_p.py

from gpanel import *

from math import *

makeGPanel(Size(950, 950))  

window(-4, 4, -4, 4)

lineWidth(1)

b = 78   

p = 1049  

n = p - 1

r = 3.8

for i in range(1,n+1):  # range(n) bedeutet: 0, 1, 2,..., n-1 

                        # range(1,n+1) bedeutet: 1, 2, 3,..., n

    s = b**i % p        #  b**i  bedeutet: b^i

    t = b**(i+1) % p

    xs = r*cos(s*2*pi/n); ys = r*sin(s*2*pi/n)

    xt = r*cos(t*2*pi/n); yt = r*sin(t*2*pi/n)

    k = (xt - xs)/10

    for j in range(0,10):  # Linie in 10 verschiedenen Farben

        xk1 = xs + j*k

        yk1 = (yt-ys)/10*j+ys

        xk2 = xs + (j+1)*k

        yk2 = (yt-ys)/10*(j+1)+ys  

        if j == 0: col = makeColor(20,20,50)     # (rot,grün,blau)     

        if j == 1: col = makeColor(120,120,150)  # 0...255

        if j == 2: col = makeColor(220,220,250)  

        if j == 3: col = makeColor(200,200,150)

        if j == 4: col = makeColor(250,250,100)

        if j == 5: col = makeColor(100,100,150)

        if j == 6: col = makeColor(100,100,100)

        if j == 7: col = makeColor(20,120,150)

        if j == 8: col = makeColor(20,200,200)

        if j == 9: col = makeColor(160,200,250)           

        setColor(col)

        line(xk1,yk1,xk2,yk2) 

2. Fall:

(b٠n) mod p mit der Basis b und der Primzahl p mit n = 1, 2, 3 … p – 1
ist ebenfalls Ausgangspunkt von Fadengrafiken.

Veranschaulichung durch Plazierung der Punkte auf dem Rand eines Kreises mit Radius r  in einem xy-Koordinatensystem nach folgender Vorschrift:

                 xs = r٠cos(n٠2π/n);  ys = r٠sin(n٠2π/n)

                 xt = r٠cos(bn mod p٠2π/n);  yt = r٠sin(bn mod p٠2π/n)

Die p – 1 verschiedenen Punkte (xs; ys) und (xt; yt) werden  dann für n = 1, 2, 3, …, p – 1 der Reihe nach mit einer geraden Linie verbunden. Dabei entstehen je nach Basis b und Primzahl p unterschiedliche Muster. Zur besseren Darstellung werden die Linien vom jeweiligen Startpunkt zum Zielpunkt im gleichen Verhältnis unterschiedlich gefärbt.

Vergleichende Beispiele:

                           a) 19ⁿ mod 53                                                        b) (19٠n) mod 53

a) 19ⁿ mod 53, n = 1, 2, …, 52:   
[19, 43, 22, 47, 45, 7, 27, 36, 48, 11, 50, 49, 30, 40, 18, 24, 32, 25, 51, 15, 20, 9, 12, 16, 39, 52, 34, 10, 31, 6, 8, 46, 26, 17, 5, 42, 3, 4, 23, 13, 35, 29, 21, 28, 2, 38, 33, 44, 41, 37, 14, 1]
z.B. 19³ / 53 = 6859 / 53 = 129 Rest 22

b) (19٠n) mod 53, n = 1, 2, …, 52:
[19, 38, 4, 23, 42, 8, 27, 46, 12, 31, 50, 16, 35, 1, 20, 39, 5, 24, 43, 9, 28, 47, 13, 32, 51, 17, 36, 2, 21, 40, 6, 25, 44, 10, 29, 48, 14, 33, 52, 18, 37, 3, 22, 41, 7, 26, 45, 11, 30, 49, 15, 34]

Die beiden Fadengrafiken sind identisch, die Ziffernfolgen sind nur unterschiedlich angeordnet, bei
Fall a: Zahlenreihenfolge  2 – 38, 3 – 4, 4 – 23, …
Fall b: Positionsreihenfolge  2 – 38, 3 – 4, 4 – 23, …

                         a) 46ⁿ mod 1049                                                       b) (46٠n) mod 1049

Bei bestimmten Werten von b und p ergeben sich bei den Fadengrafiken keine Unterschiede zwischen den beiden Fällen.

                     a) 9ⁿ mod 17                                                            b) (9٠n) mod 17 

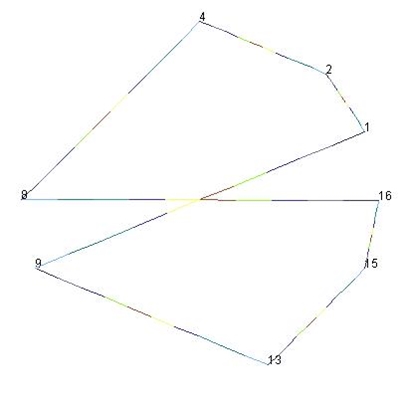
Fall a:  9ⁿ mod 17, n = 1, 2, …, 16:   [9, 13, 15, 16, 8, 4, 2, 1]  ist als Menge Teilmenge von

Fall b:  (9٠n) mod 17, n = 1, 2, …, 16:  [9, 1, 10, 2, 11, 3, 12, 4, 13, 5, 14, 6, 15, 7, 16, 8]

                  a) 19ⁿ mod 54                                                            b) (19٠n) mod 54

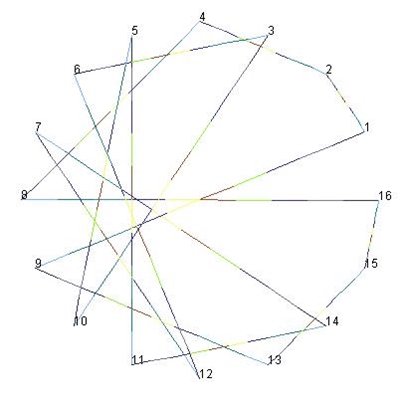
Fall a:  19ⁿ mod 54, n = 1, 2, …, 53:  [19, 37, 1]  ist als Menge Teilmenge von

Fall b:  (19٠n) mod 54, n = 1, 2, …, 53:
[19, 38, 3, 22, 41, 6, 25, 44, 9, 28, 47, 12, 31, 50, 15, 34, 53, 18, 37, 2, 21, 40, 5, 24, 43, 8, 27, 46, 11, 30, 49, 14, 33, 52, 17, 36, 1, 20, 39, 4, 23, 42, 7, 26, 45, 10, 29, 48, 13, 32, 51, 16, 35]

Die natürliche Zahl b heißt Primitivwurzel modulo Primzahl p, wenn
bⁿ mod p für n = 1, 2, 3, …, p – 1

p – 1 verschiedene natürliche Zahlen kleiner p liefert.

Vermutung:

Wenn die Basis b eine Primitivwurzel der Primzahl p ist, dann stimmen die Fadengrafiken in beiden Fällen überein. Die beiden Zahlenmengen für
bⁿ mod p  und  b٠n mod p  für n = 1, 2, 3, …, p – 1  stimmen dann überein.

Ansonsten ist die Fadengrafik zu bⁿ mod p eine Teilmenge der  Fadengrafik zu  b٠n mod p auch für den Fall, dass p keine Primzahl ist.

Programmänderung für den 2. Fall:

. . .

for i in range(1,n):

    s = i % p

    t = b*i % p

        . . .

Quelle:

http://plouffe.fr/Inverseofprimes/La%20forme%20de%20bn%20mod%20p.pdf