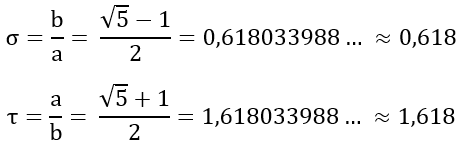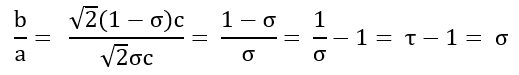|
Rechtecke und DIN A4
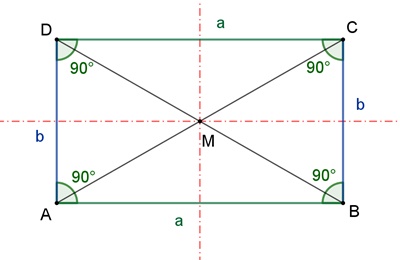
Allgemeines Rechteck
1.
Gegenüberliegende Seiten sind gleich lang und parallel.
2.
Die Innenwinkel sind jeweils 90°.
3.
Die Diagonalen sind gleich lang und halbieren sich gegenseitig.
4.
Das Rechteck hat zwei Symmetrieachsen.
5.
Das Rechteck hat einen Umkreis und ist deshalb ein Sehnenviereck.
Das Rechteck ist ein spezielles Parallelogramm mit Innenwinkel 90°.
Flächeninhalt A =
a٠b
Umfang U =
2٠(a + b)
Länge der Diagonalen
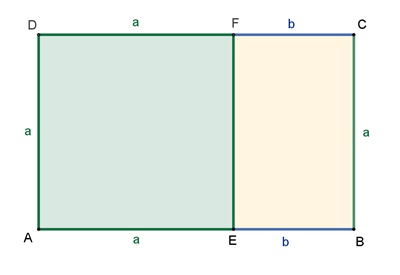
Goldenes Rechteck
Rechtecke mit der Eigenschaft a : (a
+ b) = b : a mit den Seitenlängen
a+b und a (Rechteck ABCD) bzw. a und b (Rechteck BCFE) nennt man goldene
Rechtecke. Als Seitenverhältnisse ergeben sich die goldenen Schnittzahlen
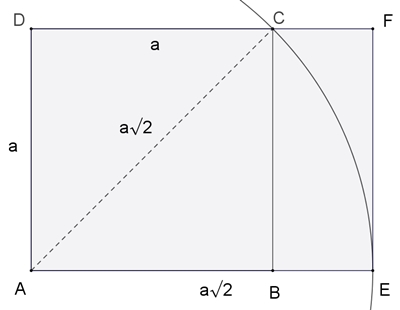
Konstruktion des goldenen Rechtecks
Begründung:
Darauf aufbauend ein Bild der Mathematikerin und Künstlerin Irene Schramm-Biermann (geb. 1950 in Detmold)
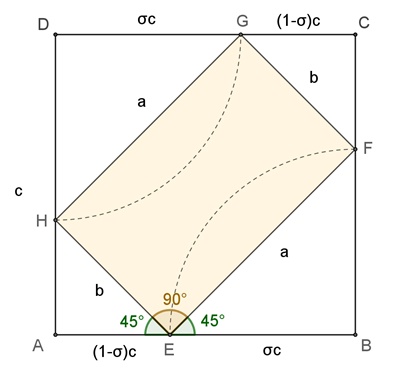
Silbernes Rechteck, Konstruktion des Silbernen Schnitts
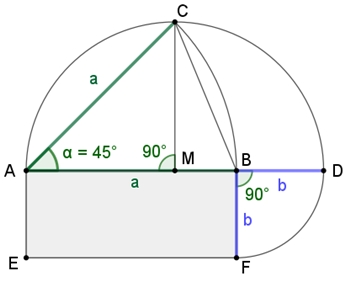
Ausgangsfigur ist gleichschenkliges Dreieck ABC mit Winkel 45°.
|AM| = a
|MB| = a – a
b =
a
b / a =
Das Rechteck EFBA heißt Silbernes Rechteck.
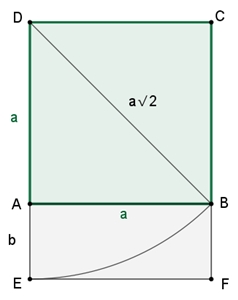
Ausgangsfigur ist ein Quadrat mit Diagonale
a
a + b = a
b = a (
b / a =
a / b =
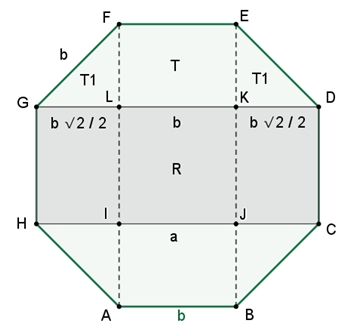
Silbernes Rechteck im regulären Achteck
a = |HC|
|GL| = b
a = b +
b
a/b = (1 +
Das Rechteck HCDG ist Silbernes Rechteck
Der Flächeninhalt des Rechtecks HCDG ist
gleich der Summe der Flächeninhalte der Trapezflächen GDEF und ABCH.
Flächeninhalt des Rechtecks HCDG: a b = b2 (1 +
Summe der Flächeninhalte der Trapezflächen: 2T + 4 T1 = b2
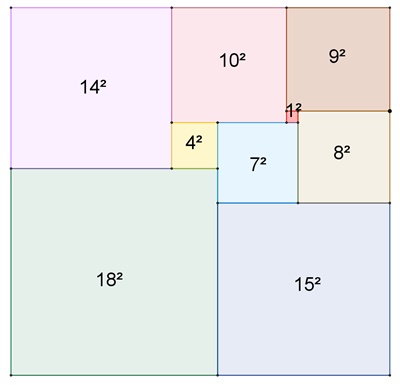
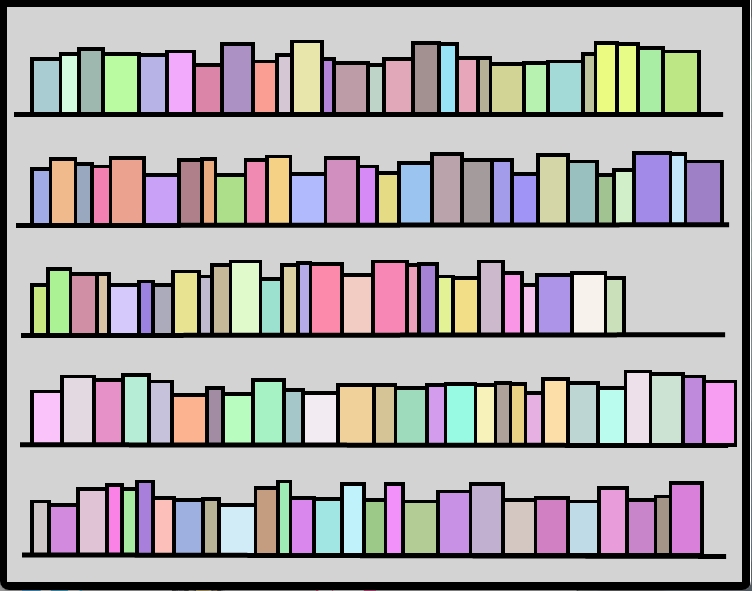
Perfektes Rechteck
Ein Rechteck heißt perfekt, wenn man es mit unterschiedlich großen Quadraten
lückenlos und überschneidungsfrei überdecken kann.
Perfektes Rechteck 33⸱32 von Zbigniew Moroń (1925)
DIN A4, Norm DIN 476 und ISO 216
Die wohl am weitesten verbreitete Norm ist die
ISO 216, ehemals
DIN 476, mit dem bekanntesten
Inhalt
DIN A4. Sie regelt inzwischen
weltweit die Größe von Papierformaten.
DIN = Deutsches
Institut für Normung
(früher: Deutsche Industrienorm)
ISO = International
Standard Organization
Bei der Norm DIN 476 gilt mit a = |AB|, b = |BC|:
|BQ| = |QC| d.h. |BQ| = ½ b
a : b = b/2 : a
a² = b²/2
a = b / √2 oder b = a √2
DIN A0:
Viereck ABCD
a = 841 mm, b = 1189 mm
Bei jedem DIN A0 – A10 Blatt gilt: Breite : Länge = 1 : √2 ≈ 1 : 1,414
DIN A1: 594 mm ٠ 841 mm
DIN A2: 420 mm
٠ 594 mm
DIN A3: 297 mm
٠ 420 mm
DIN A4: 210 mm
٠ 297 mm
DIN A5: 148 mm
٠ 210 mm
DIN A6: 105 mm
٠ 148 mm
DIN A7: 74 mm
٠ 105 mm
DIN A8: 52 mm
٠
74 mm
DIN A9: 37 mm
٠
52 mm
DIN A10: 26 mm
٠
37 mm
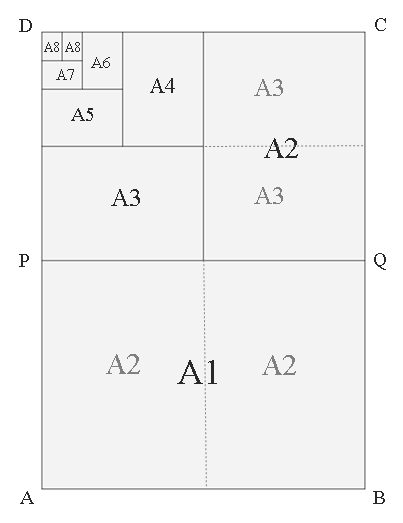
Die Blattformate in der DIN-Reihe A ergeben sich jeweils durch Halbieren des
vorhergehenden Formats.
Der Flächeninhalt des nachfolgenden Rechtecks ist dann halb so groß.
Dabei ist das Ausgangsblatt dem nächstkleineren
Blatt ähnlich. Die Geschichte von DIN A4
Im Laufe der Geschichte gab es
verschiedene Papierformate, zB. 3 : 4 oder 2 : 3.
Der Mathematiker, Physiker und
Naturforscher Georg Christoph
Lichtenberg hat bereits 1786 vorgeschlagen, das Verhaältnis 1 : √2, √2 ≈
1,414, als Seitenverhältnis eines Papierformats zu verwenden. Es wurde auch
zur Zeit der Französischen Revolution
angewendet, geriet danach aber in Vergessenheit.
Der Chemiker und Nobelpreisträger
Dr. Wilhelm Ostwald hat sich ab
1910 auch mit Papierformaten beschäftigt. Die Formate sollten zueinander
ähnlich sein, d.h. die Verhältnisse der Seitenlängen sollten gleich bleiben.
Grundlegende Seitenlänge ist 1 cm.
Dr. Walter Porstmann, Assistent von Wilhelm Ostwald, entwickelte darauf aufbauend ein
Formatsystem, welches er nicht über die Seitenlänge der Papierformate, wie
es Oswald gefordert hatte, sondern über den Flächeninhalt festlegte.
Porstmann legte 1 m² für DIN A0 als
Ausgangsmaß fest. Porstmann wurde 1920 Mitarbeiter des 1917
gegründeten Normenausschusses der Deutschen Industrie, Vorläufer
des Deutschen Instituts für Normung.
Das Deutsche Institut für Normung hat
dann am 18. August 1922 als
DIN 476 die
DIN A-, B-, C- und D-Reihe als Papierformate festgelegt. Die
DIN A-, B- und C-Reihe wurde
1975 als internationaler Standard
für Papierformate als ISO 216
übernommen. Dieser Standard gilt heute in den meisten Ländern der Welt mit
Ausnahme z.B. von USA und Kanada.
DIN B-Reihe:
DIN B0 Flächeninhalt 1,141 m² ≈ √2 m².
Bei DIN B, C und D gelten die gleichen
Verhältnisse der Seitenlängen wie bei DIN A.
Konstruktion eines DIN A Rechtecks bei gegebenen Breite a
E liegt:
Das Rechteck AEFD ist ein DIN A Rechteck.
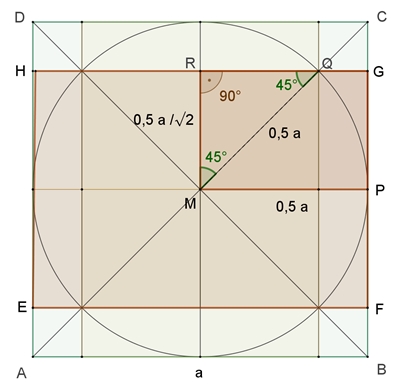
Gegeben ist ein Quadrat ABCD mit der
Seitenlänge a, seine Diagonalen mit Mittelpunkt M und die Senkrechten zu den
Seiten des Quadrats durch M.
Der Kreis um M mit Radius a/2 schneidet die
Diagonalen in 4 Punkten, durch die jeweils Parallelen zu den Seiten gezogen
werden.
Das Dreieck MQR ist gleichschenklig
rechtwinklig mit der Hypotenuse 0,5a und den Katheten 0,5a/√2 (Pythagoras im
ΔMQR).
Mit a = 297 mm ist EFGH ein DIN A4 Rechteck
und MPGR ein DIN A6 Rechteck.
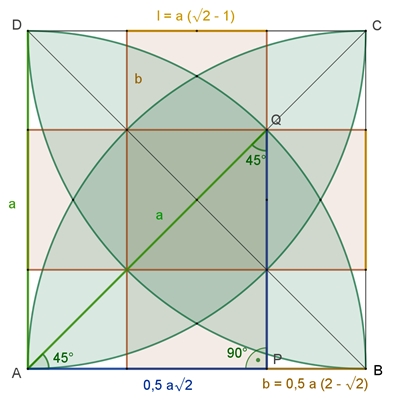
DIN A5 im
Quadrat mit Kreisbögen
Gegeben ist ein Quadrat ABCD mit der Seitenlänge a und seine Diagonalen.
Das gleichschenklig rechtwinklige Dreieck APQ mit der Hypotenuse a hat die
Katheten der Länge 0,5 a √2.
b = a – 0,5a√2 = 0,5a (2 – √2)
l = a – 2٠0,5a (2 – √2) = a (√2 – 1)
Länge l : Breite b:
l : b = a (√2 – 1) : (0,5a (2 – √2))
l : b = 2(√2 – 1) : (2 – √2)
Ein Quadrat ABCD mit der Seitenlänge a = 507 mm besitzt dann in obiger Figur
4 gleich große DIN A5 Rechtecke. Stilisierte Bücherwand mit Rechtecken Treppen
Zurück Zurück zur Startseite |