Grenzwert zweier verknüpfter Rekursionen

I    u_n+1 = (u_n + v_n) / 2    
II  v_n+1 = ,

mit  u₀ = a  und  v₀ = b

Behauptung:  Für n → ∞ gilt:  u_∞ = v_∞ und  u_∞ = 2

Begründung:

Falls ein Grenzwert existiert, gilt für große Werte von n:
u_n+1 ≈ (u_n + v_n) / 2    und   v_n+1 ≈

Ansatz zu I:

u = (u + v)/2
2u = u + v
u = v

Ansatz zu II:

v =    | □²
v² = u + v   |  u = v
v² = 2v   | : v ≠ 0
v = 2

Ergebnis: Der gemeinsame Grenzwert von u_n und v_n für n → ∞  ist 2, unabhängig von a und b.

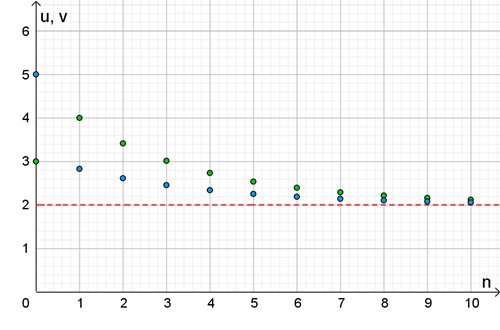
Graphische Darstellung für u₀ = a = 3 und v₀ = b = 5

u₁ = (3 + 5)/2 = 4; v₁ = √8 ≈ 2,83
u₂ ≈ 3,41;  v₂ ≈ 2,61
…